正弦定理和余弦定理
图片预览



文档简介
课件15张PPT。第一章 解三角形1.1正弦定理授课人:杨刚引例 如图:设A,B两点在河的两岸,要测量两点之间的距离.测量者在A的同侧, 选定一点C,测出A,C两点间的距离是50m,∠ACB=600,∠BAC=750,求A,B两点间的距离.ACB创设情境转化将实际问题转化为数学问题:
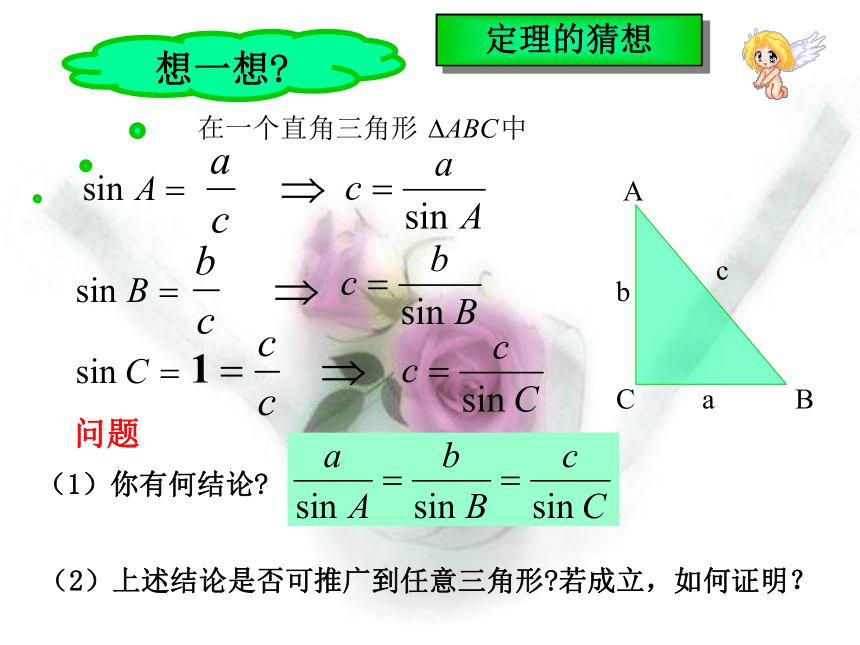
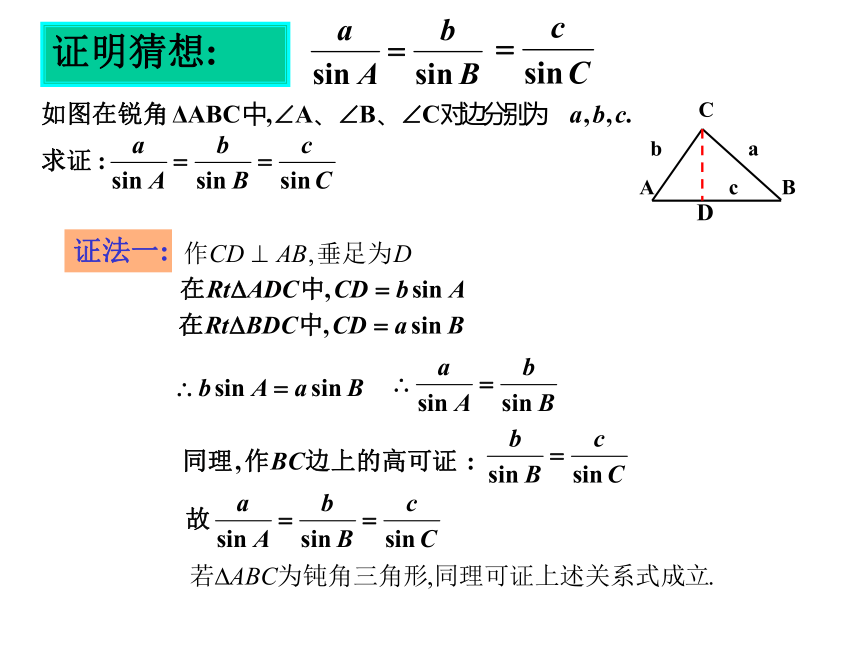
A.B..CbA.B..Cb已知三角形的两个角和一条边,求另一条边。已知:b=50,∠C=600,∠A=750,求AB边。已知三角形的几个元素,求其它元素的过程叫做解三角形。ACBcba想一想?问题 (2)上述结论是否可推广到任意三角形?若成立,如何证明?(1)你有何结论?定理的猜想证明猜想: C
b a
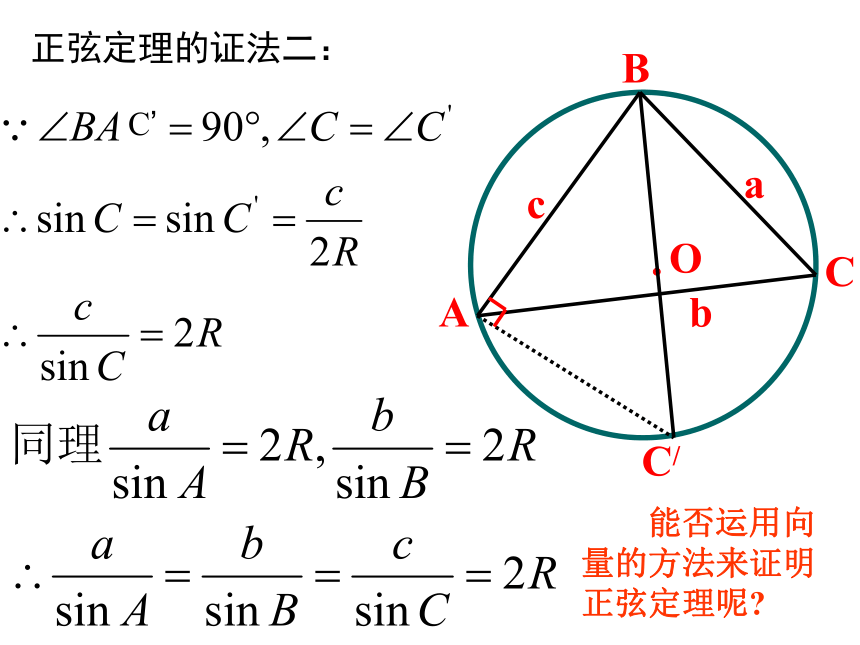
A c B证法一:D正弦定理的证法二: 能否运用向量的方法来证明正弦定理呢?C’(1)文字叙述正弦定理:在一个三角形中,各边和它所对角 的正弦的比相等.(2)结构特点(3)方程的观点正弦定理实际上是已知其中三个,求另一个.和谐美、对称美.正弦定理:解:正弦定理应用一:
已知两角和任意一边,求其余两边和一角 理解·应用
1、在⊿ABC中,A=600,B=450,a=9,求边b
2、已知A=300,B-C=600,a=2,求边c 练习·巩固实际应用将实际问题转化为数学问题:
A.B..CbA.B..Cb已知三角形的两个角和一条边,求另一条边。已知:b=50,∠C=600,∠A=750,求AB边。
正弦定理应用二:
已知两边和其中一边对角,求另一边的对角,进
而可求其它的边和角。(要注意解的情况)
要点:已知两边和其中一边的对角解三角形时,通常要用到三角形内角和定理或大边对大角定理等三角形有关性质.定理应用 归纳小结二个 —— 已知两角和一边(只有一解)
已知两边和其中一边的对角
(有一解,两解,无解) 作业:P5 练习 1, 2思考题:
A.B..CbA.B..Cb已知三角形的两个角和一条边,求另一条边。已知:b=50,∠C=600,∠A=750,求AB边。已知三角形的几个元素,求其它元素的过程叫做解三角形。ACBcba想一想?问题 (2)上述结论是否可推广到任意三角形?若成立,如何证明?(1)你有何结论?定理的猜想证明猜想: C
b a
A c B证法一:D正弦定理的证法二: 能否运用向量的方法来证明正弦定理呢?C’(1)文字叙述正弦定理:在一个三角形中,各边和它所对角 的正弦的比相等.(2)结构特点(3)方程的观点正弦定理实际上是已知其中三个,求另一个.和谐美、对称美.正弦定理:解:正弦定理应用一:
已知两角和任意一边,求其余两边和一角 理解·应用
1、在⊿ABC中,A=600,B=450,a=9,求边b
2、已知A=300,B-C=600,a=2,求边c 练习·巩固实际应用将实际问题转化为数学问题:
A.B..CbA.B..Cb已知三角形的两个角和一条边,求另一条边。已知:b=50,∠C=600,∠A=750,求AB边。
正弦定理应用二:
已知两边和其中一边对角,求另一边的对角,进
而可求其它的边和角。(要注意解的情况)
要点:已知两边和其中一边的对角解三角形时,通常要用到三角形内角和定理或大边对大角定理等三角形有关性质.定理应用 归纳小结二个 —— 已知两角和一边(只有一解)
已知两边和其中一边的对角
(有一解,两解,无解) 作业:P5 练习 1, 2思考题:
