苏教版五年级下册数学1.3 等式的性质(2)和解方程课件(共33张PPT)
文档属性
| 名称 | 苏教版五年级下册数学1.3 等式的性质(2)和解方程课件(共33张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-26 13:26:24 | ||
图片预览







文档简介
(共33张PPT)
简易方程
等式的性质(2)和解方程
苏教版五年级下册数学
1.进一步理解并掌握等式的性质,即在等式两边同时乘或除以同一个不等于0的数,结果仍然是等式。
2.掌握利用等式的性质解一步计算的方程,进一步培养代数思维。
学习目标
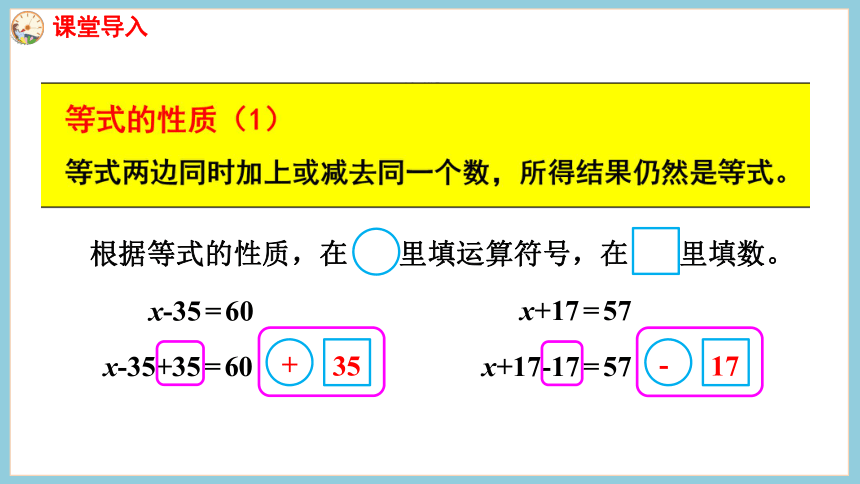
x-35=60
x-35+35=60
x+17=57
x+17-17=57
根据等式的性质,在 里填运算符号,在 里填数。
+
35
-
17
课堂导入
5
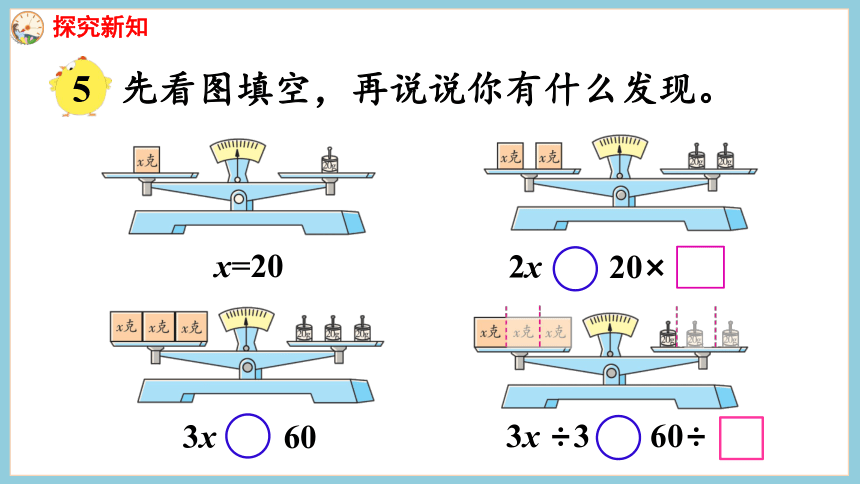
先看图填空,再说说你有什么发现。
x=20
2x
20×
3x
60
3x ÷3 60÷
探究新知
20×2
x克
x
20
=
x克
天平两边放上同样重的物体,天平仍然保持平衡。
x+x
=
20+20
求几个相同加数连加的和,可以用乘法计算。
2x
20×2
x克
x
20
=
x克
天平两边放上同样重的物体,天平仍然保持平衡。
=
等式两边同时乘同一个数,得到的结果仍然是等式。
2x
x克
x克
x克
3x 60
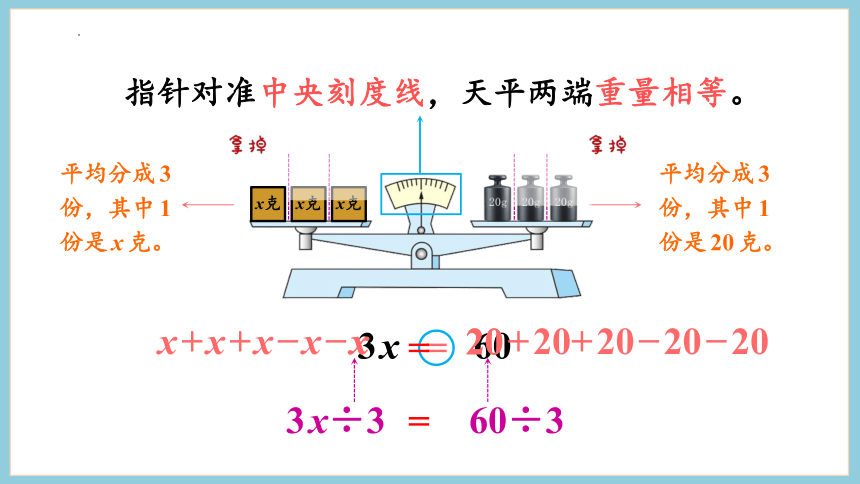
指针对准中央刻度线,天平两端重量相等。
=
平均分成3份,其中1份是x克。
平均分成3份,其中1份是20克。
x+x+x x x
20+20+20 20 20
x
20
=
3x÷3
60÷3
=
x=20 2x=20×2
3x=60 3x÷3=60÷3
等式两边同时乘同一个数,得到的结果仍然是等式。
等式两边同时除以一个数,得到的结果仍然是等式。
5
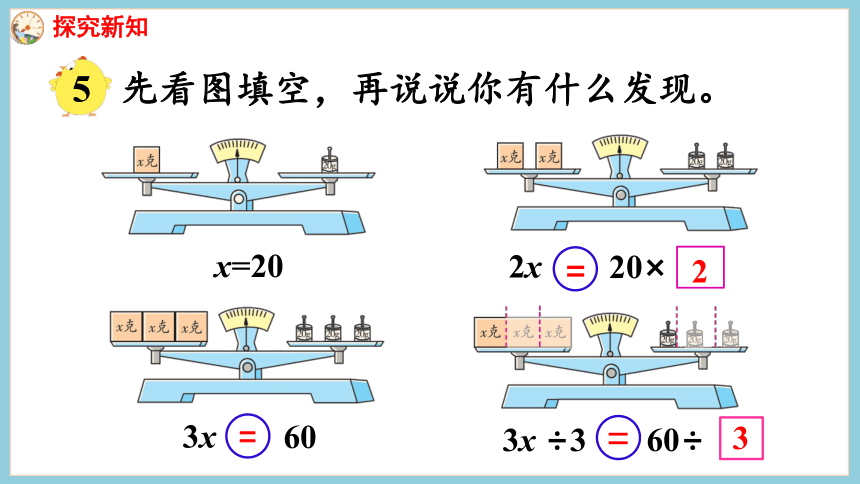
先看图填空,再说说你有什么发现。
=
2
x=20
2x
20×
=
3
3x
60
=
3x ÷3 60÷
探究新知
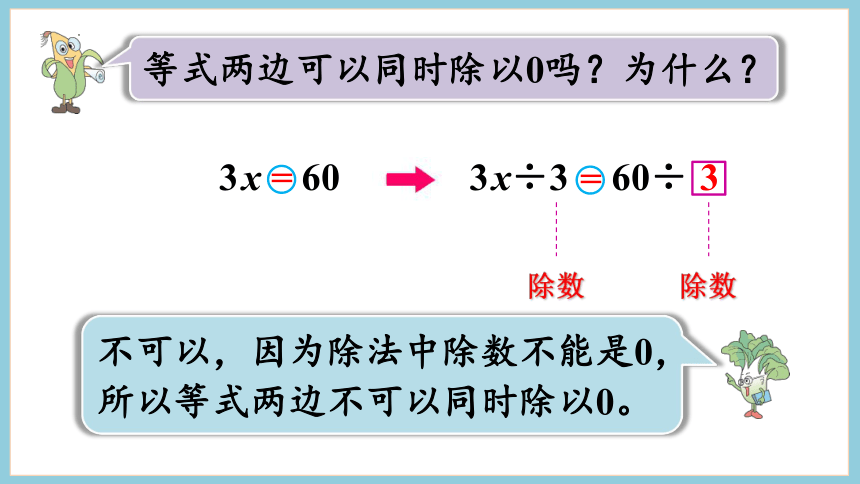
等式两边可以同时除以0吗?为什么?
3x 60
3x÷3 60÷
=
=
3
除数
除数
不可以,因为除法中除数不能是0,所以等式两边不可以同时除以0。
等式的性质
等式两边同时乘或除以同一个不是0的数,所得结果仍然是等式。
根据等式的性质在 里填运算符号,在 里填数。
x÷6=18
x ÷6 × 6 =18
×
6
0.7x =3.5
0.7x ÷ 0.7x =3.5
÷
0.7
试一试
6
花园小学有一块长方形试用田(如下图),求试验田的宽。
你打算怎样做?与同学交流。
长方形的面积÷长=宽,960÷40=24(米)。
长×宽=长方形的面积,可以列方程解答。
40x = 960
解:40x ÷ 40 = 960 ÷ 40
x = 24
方程两边为什么都要除以40?
等式的两边同时除以一个数,得到的结果仍然是等式。
检验一下,看解答结果是否正确。
检验:
把x = 14代入原方程,
左边=40×14=960,
左边=右边,
所以x = 14是原方程的解。
答:试验田的宽是14米。
1. 解形如ax=b(a≠0)的方程时,
要根据等式的性质(2),将方
程两边同时除以a。
小结
解: ax÷a =b÷a
x=b÷a
ax =b
2. 解形如x÷a=b(a≠0)的方程,
要根据等式的性质(2),方程
两边同时乘a。
解: x÷a×a =b×a
x= b×a
x÷a =b
解方程 x÷0.2=0.8。
解:x ÷0.2×0.2=0.8×0.2
x = 0.16
x ÷0.2 = 0.8
检验:
把x = 0.16代入原方程,
左边=0.16÷0.2=0.8,
左边=右边,
所以x = 0.16是原方程的解。
练一练
1. 要使下面每个方程的左边只剩下x,方程的两边应同时乘或除以几
(1)x×2.3=20.7
方程两边应同时( 除以2.3 )。
(2)x÷4=1.25
方程两边应同时( 乘4 )。
除以2.3
乘4
课堂练习
2. 根据等式的性质在 里填正确的运算符号,在 里填数。
(1) x÷7=5
x÷7×7=5 × 7
x= 35
×
7
35
(2) 9x=63
9x÷9=63 ÷ 9
x= 7
÷
9
7
x÷40 = 14
解:x ÷40×40 = 14×40
x = 560
检验:
把x = 560代入原方程,
左边=560÷40=14,
左边=右边,
所以x = 560是原方程的解。
3.解方程并检验。
18x = 3.6
解:18x÷18= 3.6÷18
x = 0.2
检验:
把x = 0.2代入原方程,
左边=18×0.2=3.6,
左边=右边,
所以x = 0.2是原方程的解。
3.解方程并检验。
x÷2.5 = 5
解:x ÷2.5×2.5 = 5×2.5
x = 12.5
检验:
把x = 12.5代入原方程,
左边=12.5÷2.5=5,
左边=右边,
所以x = 12.5是原方程的解。
3.解方程并检验。
4. 看图列方程,并解答。
(1)
x÷0.18=32
x=5.76
(2)
8x=20
x=2.5
(3)
4x=12 解得x=3
(4)
20x÷2=192 解得x=19.2
5.下面是某学校食堂购物的票据单,你能根据表格求出x、
y、z的值吗?
商品 单价 数量 总价
面包 x元/千克 25千克 70.00元
油 8.00元/升 y升 z元
合计金额:132.40元
25x=70
解得x=2.8
70+z=132.4
解得z=62.4
8y=62.4
解得y=7.8
6.在( )里填上合适的数,使天平保持平衡,
并用数量关系式说明理由。
6
理由:因为2根香蕉的质量=4颗草莓的质量,所以1根
香蕉的质量=2颗草莓的质量,因为1个苹果的质量=3
根香蕉的质量,所以1个苹果的质量=6颗草莓的质量。
提升练习
7. 在括号里填合适的数,使每个方程的解都是x=8。
x×( 1.25 )=10 ( 80 )÷x=10
x×( 2.5 )÷2=10 ( 160 )÷x÷2=10
[提示]将x=8代入方程,把括号中的数看作未知数,并解方程。
1.25
80
2.5
160
8. 一个平行四边形和一个三角形等底等面积,且底都是6厘米。平行四边形的面积是12平方厘米,三角形该底边上的高是x厘米。你能求出这个三角形该底边上的高是多少厘米吗
6x÷2=12 x=4
[提示]一个平行四边形和一个三角形等底等面积,知道了平行四边形的面积,也就知道了三角形的面积。已知三角形的底和面积,从而可根据三角形的面积公式列出方程。
1.已知关于x的方程ax=48与x÷3.2=5的解相同,求a-
1.8的值。
x÷3.2=5
解得x=16
把x=16代入方程ax=48
解得a=3
a-1.8=3-1.8=1.2
思维拓展
2.李老师的汽车车牌号如图。已知○+○=□,○+□+
□=15,△+△+△=○,那么李老师的汽车车牌号的后
三位数分别是( 3 )、( 6 )、( 1 )。
3
6
1
这节课你有什么收获?
等式两边同时乘或除以同一个不是0的数,所得的结果仍然是等式。这是等式的性质(2)。
课堂小结
ɑx=b x÷a =b
解:ax÷a =b÷ɑ 解:x÷a×a =b×ɑ
x =b÷ɑ x =b×ɑ
形如ɑx=b和x÷a =b的方程的解法
这节课你有什么收获?
课堂小结
简易方程
等式的性质(2)和解方程
苏教版五年级下册数学
1.进一步理解并掌握等式的性质,即在等式两边同时乘或除以同一个不等于0的数,结果仍然是等式。
2.掌握利用等式的性质解一步计算的方程,进一步培养代数思维。
学习目标
x-35=60
x-35+35=60
x+17=57
x+17-17=57
根据等式的性质,在 里填运算符号,在 里填数。
+
35
-
17
课堂导入
5
先看图填空,再说说你有什么发现。
x=20
2x
20×
3x
60
3x ÷3 60÷
探究新知
20×2
x克
x
20
=
x克
天平两边放上同样重的物体,天平仍然保持平衡。
x+x
=
20+20
求几个相同加数连加的和,可以用乘法计算。
2x
20×2
x克
x
20
=
x克
天平两边放上同样重的物体,天平仍然保持平衡。
=
等式两边同时乘同一个数,得到的结果仍然是等式。
2x
x克
x克
x克
3x 60
指针对准中央刻度线,天平两端重量相等。
=
平均分成3份,其中1份是x克。
平均分成3份,其中1份是20克。
x+x+x x x
20+20+20 20 20
x
20
=
3x÷3
60÷3
=
x=20 2x=20×2
3x=60 3x÷3=60÷3
等式两边同时乘同一个数,得到的结果仍然是等式。
等式两边同时除以一个数,得到的结果仍然是等式。
5
先看图填空,再说说你有什么发现。
=
2
x=20
2x
20×
=
3
3x
60
=
3x ÷3 60÷
探究新知
等式两边可以同时除以0吗?为什么?
3x 60
3x÷3 60÷
=
=
3
除数
除数
不可以,因为除法中除数不能是0,所以等式两边不可以同时除以0。
等式的性质
等式两边同时乘或除以同一个不是0的数,所得结果仍然是等式。
根据等式的性质在 里填运算符号,在 里填数。
x÷6=18
x ÷6 × 6 =18
×
6
0.7x =3.5
0.7x ÷ 0.7x =3.5
÷
0.7
试一试
6
花园小学有一块长方形试用田(如下图),求试验田的宽。
你打算怎样做?与同学交流。
长方形的面积÷长=宽,960÷40=24(米)。
长×宽=长方形的面积,可以列方程解答。
40x = 960
解:40x ÷ 40 = 960 ÷ 40
x = 24
方程两边为什么都要除以40?
等式的两边同时除以一个数,得到的结果仍然是等式。
检验一下,看解答结果是否正确。
检验:
把x = 14代入原方程,
左边=40×14=960,
左边=右边,
所以x = 14是原方程的解。
答:试验田的宽是14米。
1. 解形如ax=b(a≠0)的方程时,
要根据等式的性质(2),将方
程两边同时除以a。
小结
解: ax÷a =b÷a
x=b÷a
ax =b
2. 解形如x÷a=b(a≠0)的方程,
要根据等式的性质(2),方程
两边同时乘a。
解: x÷a×a =b×a
x= b×a
x÷a =b
解方程 x÷0.2=0.8。
解:x ÷0.2×0.2=0.8×0.2
x = 0.16
x ÷0.2 = 0.8
检验:
把x = 0.16代入原方程,
左边=0.16÷0.2=0.8,
左边=右边,
所以x = 0.16是原方程的解。
练一练
1. 要使下面每个方程的左边只剩下x,方程的两边应同时乘或除以几
(1)x×2.3=20.7
方程两边应同时( 除以2.3 )。
(2)x÷4=1.25
方程两边应同时( 乘4 )。
除以2.3
乘4
课堂练习
2. 根据等式的性质在 里填正确的运算符号,在 里填数。
(1) x÷7=5
x÷7×7=5 × 7
x= 35
×
7
35
(2) 9x=63
9x÷9=63 ÷ 9
x= 7
÷
9
7
x÷40 = 14
解:x ÷40×40 = 14×40
x = 560
检验:
把x = 560代入原方程,
左边=560÷40=14,
左边=右边,
所以x = 560是原方程的解。
3.解方程并检验。
18x = 3.6
解:18x÷18= 3.6÷18
x = 0.2
检验:
把x = 0.2代入原方程,
左边=18×0.2=3.6,
左边=右边,
所以x = 0.2是原方程的解。
3.解方程并检验。
x÷2.5 = 5
解:x ÷2.5×2.5 = 5×2.5
x = 12.5
检验:
把x = 12.5代入原方程,
左边=12.5÷2.5=5,
左边=右边,
所以x = 12.5是原方程的解。
3.解方程并检验。
4. 看图列方程,并解答。
(1)
x÷0.18=32
x=5.76
(2)
8x=20
x=2.5
(3)
4x=12 解得x=3
(4)
20x÷2=192 解得x=19.2
5.下面是某学校食堂购物的票据单,你能根据表格求出x、
y、z的值吗?
商品 单价 数量 总价
面包 x元/千克 25千克 70.00元
油 8.00元/升 y升 z元
合计金额:132.40元
25x=70
解得x=2.8
70+z=132.4
解得z=62.4
8y=62.4
解得y=7.8
6.在( )里填上合适的数,使天平保持平衡,
并用数量关系式说明理由。
6
理由:因为2根香蕉的质量=4颗草莓的质量,所以1根
香蕉的质量=2颗草莓的质量,因为1个苹果的质量=3
根香蕉的质量,所以1个苹果的质量=6颗草莓的质量。
提升练习
7. 在括号里填合适的数,使每个方程的解都是x=8。
x×( 1.25 )=10 ( 80 )÷x=10
x×( 2.5 )÷2=10 ( 160 )÷x÷2=10
[提示]将x=8代入方程,把括号中的数看作未知数,并解方程。
1.25
80
2.5
160
8. 一个平行四边形和一个三角形等底等面积,且底都是6厘米。平行四边形的面积是12平方厘米,三角形该底边上的高是x厘米。你能求出这个三角形该底边上的高是多少厘米吗
6x÷2=12 x=4
[提示]一个平行四边形和一个三角形等底等面积,知道了平行四边形的面积,也就知道了三角形的面积。已知三角形的底和面积,从而可根据三角形的面积公式列出方程。
1.已知关于x的方程ax=48与x÷3.2=5的解相同,求a-
1.8的值。
x÷3.2=5
解得x=16
把x=16代入方程ax=48
解得a=3
a-1.8=3-1.8=1.2
思维拓展
2.李老师的汽车车牌号如图。已知○+○=□,○+□+
□=15,△+△+△=○,那么李老师的汽车车牌号的后
三位数分别是( 3 )、( 6 )、( 1 )。
3
6
1
这节课你有什么收获?
等式两边同时乘或除以同一个不是0的数,所得的结果仍然是等式。这是等式的性质(2)。
课堂小结
ɑx=b x÷a =b
解:ax÷a =b÷ɑ 解:x÷a×a =b×ɑ
x =b÷ɑ x =b×ɑ
形如ɑx=b和x÷a =b的方程的解法
这节课你有什么收获?
课堂小结
