第三十二章 投影与视图 复习课课件(共17张PPT)2023-2024学年冀教版九年级数学下册
文档属性
| 名称 | 第三十二章 投影与视图 复习课课件(共17张PPT)2023-2024学年冀教版九年级数学下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 640.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-27 08:24:44 | ||
图片预览





文档简介
(共17张PPT)
第三十二章 投影与视图
复习课
典型例题
当堂检测
学习目标
课堂总结
知识梳理
1.掌握中心投影与平行投影的区别与联系,理解正投影的概念
2.明确三视图的意义,会画简单物体的三视图
3.能够根据三视图还原简单几何体
4.了解直棱柱和圆锥的侧面展开图,并进行简单计算
典型例题
当堂检测
学习目标
课堂总结
知识梳理
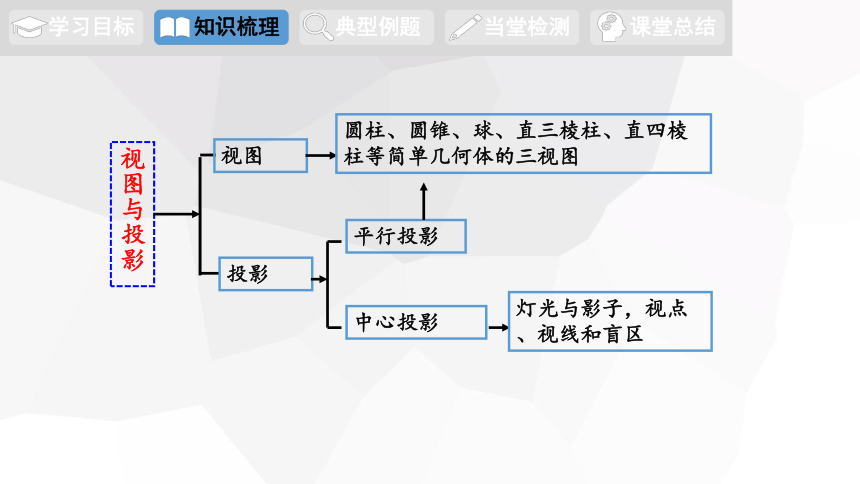
中心投影
视图与投影
视图
投影
平行投影
灯光与影子,视点、视线和盲区
圆柱、圆锥、球、直三棱柱、直四棱柱等简单几何体的三视图
典型例题
当堂检测
学习目标
课堂总结
知识梳理
平行投影与中心投影
1
在同一时刻,物体高度与影子长度成比例.
物体的三视图实际上就是该物体在某一平行光线(垂直于投影面的平行光线)下的平行投影.
1.太阳光线可以看成平行光线,像这样的光线所形成的投影称为平行投影.
皮影和手影都是在灯光照射下形成的影子.它们是中心投影
2.探照灯,手电筒,路灯,和台灯的光线可以看成是从一点出发的光线,像这样的光线所形成的投影称为中心投影.
典型例题
当堂检测
学习目标
课堂总结
知识梳理
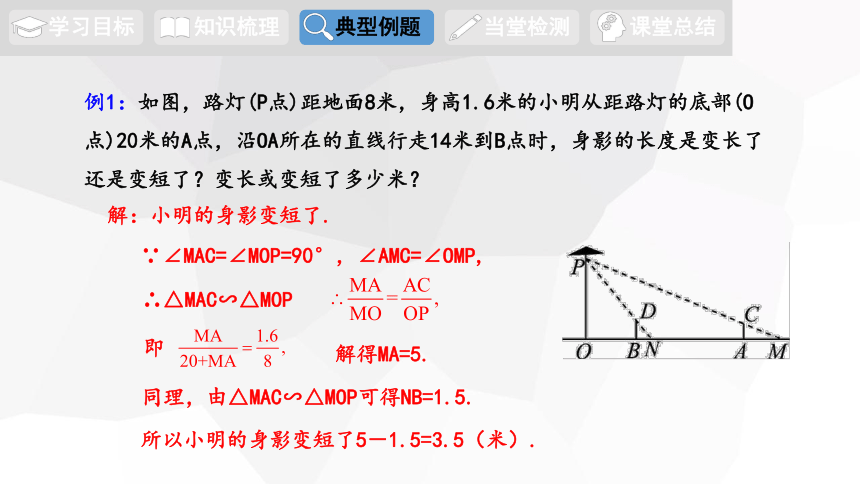
例1:如图,路灯(P点)距地面8米,身高1.6米的小明从距路灯的底部(O点)20米的A点,沿OA所在的直线行走14米到B点时,身影的长度是变长了还是变短了?变长或变短了多少米?
解:小明的身影变短了.
∵∠MAC=∠MOP=90°,∠AMC=∠OMP,
∴△MAC∽△MOP
即
解得MA=5.
同理,由△MAC∽△MOP可得NB=1.5.
所以小明的身影变短了5-1.5=3.5(米).
典型例题
当堂检测
学习目标
课堂总结
知识梳理
1.下列结论正确的有( )
①同一时刻,物体在阳光照射下,影子的方向是相同的;
②物体在任何光线照射下影子的方向都是相同的;
③物体在路灯照射下,影子的方向与路灯的位置有关;
④物体在光线照射下,影子的长短仅与物体的长短有关.
A.1个 B.2个
C.3个 D.4个
B
典型例题
当堂检测
学习目标
课堂总结
知识梳理
2. 如图,小明与同学合作利用太阳光线测量旗杆的高度,身高1.6m的小明落在地面上的影长为BC=2.4m.
(1)请你在图中画出旗杆在同一时刻阳光照射下落在地面上的影子EG;
(2)若小明测得此刻旗杆落在地面的影长EG=16m,请求出旗杆DE的高度.
解:(1)连结AC,过D点作DG∥AC交BC于G点,则GE为所求;
(2)∵DG∥AC,∴∠G=∠C,
∴Rt△ABC∽△RtDEG,
∴ ,
即 ,解得 ,
∴旗杆的高度为 m.
G
典型例题
当堂检测
学习目标
课堂总结
知识梳理
②在画图时,看的见部分的轮廓通常画成实线,看不见部分的轮廓线通常画成虚线.
画物体的三视图时,要符合如下原则:①长对正,高平齐,宽相等.
俯视图——从上面看到的图
左视图——从左面看到的图
主视图——从正面看到的图
三视图
2
典型例题
当堂检测
学习目标
课堂总结
知识梳理
例2:如下方左图,是由大小相同的5个小正方体搭成的几何体,则它的主视图是( ).
【解析】B 根据三视图的定义,几何体的主视图应该从前面向后看,所以本题看到的平面图形应该是选项B,选项A是该几何体的左视图,选项C是该几何体的俯视图.
B
典型例题
当堂检测
学习目标
课堂总结
知识梳理
3.从不同方向看一只茶壶,你认为是俯视效果图的是( )
A
方法归纳:
根据几何体选择视图,观察几何体时,要正对着几何体,视线要与放置几何体的平面持平,俯视图反映了物体的长和宽,主视图反映了物体的长和高,左视图反映了物体的高和宽.
典型例题
当堂检测
学习目标
课堂总结
知识梳理
例4:已知一个几何体的三视图如图所示,则该几何体是( )
A.棱柱 B.圆柱 C.圆锥 D.球
【解析】B;由三个方向看到的平面图形说出立体图形,首先抓住俯视图,再结合另两个视图就得出立体图形的名称.
B
典型例题
当堂检测
学习目标
课堂总结
知识梳理
4.如图所示的三视图所对应的几何体是( )
D
典型例题
当堂检测
学习目标
课堂总结
知识梳理
直棱柱和圆锥的侧面展开图
3
1.直棱柱的侧面展开图是矩形,其面积=直棱柱的底面周长×直棱柱的高.
2.圆锥侧面积公式:S侧=πrl(r为底面圆半径,l为母线长)
3.圆锥全面积公式:S全= (r为底面圆半径,l为母线长)
典型例题
当堂检测
学习目标
课堂总结
知识梳理
例5:某工厂要加工一批密封罐,设计者给出了密封罐的三视图,请你按照三视图确定制作每个密封罐所需钢板的面积.
分析:对于某些立体图形,沿着其中一些线(例如棱柱的棱)剪开,可以把立体图形的表面展开成一个平面图形——展开图.在实际的生产中,三视图和展开图往往结合在一起使用.解决本题的思路是,由三视图想象出密封罐的立体形状,再进一步画出展开图,从而计算面积.
100
50
50
100
典型例题
当堂检测
学习目标
课堂总结
知识梳理
解:由三视图可知,密封罐的现状是正六棱柱.
密封罐的高为50mm,店面正六边形的直径为100mm,边长为50mm,图是它的展开图.
由展开图可知,制作一个密封罐所需钢板的面积为
(mm2)
典型例题
当堂检测
学习目标
课堂总结
知识梳理
5.我国古代数学著作《九章算术》中,将底面是直角三角形,且侧棱与底面垂直的三棱柱称为“堑堵”.某“堑堵”的三视图如图所示(网格图中每个小正方形的边长均为1),则该“堑堵”的侧面积为( )
A. B.
C. D.
A
典型例题
当堂检测
学习目标
课堂总结
知识梳理
中心投影
视图与投影
视图
投影
平行投影
灯光与影子,视点、视线和盲区
圆柱、圆锥、球、直三棱柱、直四棱柱等简单几何体的三视图
第三十二章 投影与视图
复习课
典型例题
当堂检测
学习目标
课堂总结
知识梳理
1.掌握中心投影与平行投影的区别与联系,理解正投影的概念
2.明确三视图的意义,会画简单物体的三视图
3.能够根据三视图还原简单几何体
4.了解直棱柱和圆锥的侧面展开图,并进行简单计算
典型例题
当堂检测
学习目标
课堂总结
知识梳理
中心投影
视图与投影
视图
投影
平行投影
灯光与影子,视点、视线和盲区
圆柱、圆锥、球、直三棱柱、直四棱柱等简单几何体的三视图
典型例题
当堂检测
学习目标
课堂总结
知识梳理
平行投影与中心投影
1
在同一时刻,物体高度与影子长度成比例.
物体的三视图实际上就是该物体在某一平行光线(垂直于投影面的平行光线)下的平行投影.
1.太阳光线可以看成平行光线,像这样的光线所形成的投影称为平行投影.
皮影和手影都是在灯光照射下形成的影子.它们是中心投影
2.探照灯,手电筒,路灯,和台灯的光线可以看成是从一点出发的光线,像这样的光线所形成的投影称为中心投影.
典型例题
当堂检测
学习目标
课堂总结
知识梳理
例1:如图,路灯(P点)距地面8米,身高1.6米的小明从距路灯的底部(O点)20米的A点,沿OA所在的直线行走14米到B点时,身影的长度是变长了还是变短了?变长或变短了多少米?
解:小明的身影变短了.
∵∠MAC=∠MOP=90°,∠AMC=∠OMP,
∴△MAC∽△MOP
即
解得MA=5.
同理,由△MAC∽△MOP可得NB=1.5.
所以小明的身影变短了5-1.5=3.5(米).
典型例题
当堂检测
学习目标
课堂总结
知识梳理
1.下列结论正确的有( )
①同一时刻,物体在阳光照射下,影子的方向是相同的;
②物体在任何光线照射下影子的方向都是相同的;
③物体在路灯照射下,影子的方向与路灯的位置有关;
④物体在光线照射下,影子的长短仅与物体的长短有关.
A.1个 B.2个
C.3个 D.4个
B
典型例题
当堂检测
学习目标
课堂总结
知识梳理
2. 如图,小明与同学合作利用太阳光线测量旗杆的高度,身高1.6m的小明落在地面上的影长为BC=2.4m.
(1)请你在图中画出旗杆在同一时刻阳光照射下落在地面上的影子EG;
(2)若小明测得此刻旗杆落在地面的影长EG=16m,请求出旗杆DE的高度.
解:(1)连结AC,过D点作DG∥AC交BC于G点,则GE为所求;
(2)∵DG∥AC,∴∠G=∠C,
∴Rt△ABC∽△RtDEG,
∴ ,
即 ,解得 ,
∴旗杆的高度为 m.
G
典型例题
当堂检测
学习目标
课堂总结
知识梳理
②在画图时,看的见部分的轮廓通常画成实线,看不见部分的轮廓线通常画成虚线.
画物体的三视图时,要符合如下原则:①长对正,高平齐,宽相等.
俯视图——从上面看到的图
左视图——从左面看到的图
主视图——从正面看到的图
三视图
2
典型例题
当堂检测
学习目标
课堂总结
知识梳理
例2:如下方左图,是由大小相同的5个小正方体搭成的几何体,则它的主视图是( ).
【解析】B 根据三视图的定义,几何体的主视图应该从前面向后看,所以本题看到的平面图形应该是选项B,选项A是该几何体的左视图,选项C是该几何体的俯视图.
B
典型例题
当堂检测
学习目标
课堂总结
知识梳理
3.从不同方向看一只茶壶,你认为是俯视效果图的是( )
A
方法归纳:
根据几何体选择视图,观察几何体时,要正对着几何体,视线要与放置几何体的平面持平,俯视图反映了物体的长和宽,主视图反映了物体的长和高,左视图反映了物体的高和宽.
典型例题
当堂检测
学习目标
课堂总结
知识梳理
例4:已知一个几何体的三视图如图所示,则该几何体是( )
A.棱柱 B.圆柱 C.圆锥 D.球
【解析】B;由三个方向看到的平面图形说出立体图形,首先抓住俯视图,再结合另两个视图就得出立体图形的名称.
B
典型例题
当堂检测
学习目标
课堂总结
知识梳理
4.如图所示的三视图所对应的几何体是( )
D
典型例题
当堂检测
学习目标
课堂总结
知识梳理
直棱柱和圆锥的侧面展开图
3
1.直棱柱的侧面展开图是矩形,其面积=直棱柱的底面周长×直棱柱的高.
2.圆锥侧面积公式:S侧=πrl(r为底面圆半径,l为母线长)
3.圆锥全面积公式:S全= (r为底面圆半径,l为母线长)
典型例题
当堂检测
学习目标
课堂总结
知识梳理
例5:某工厂要加工一批密封罐,设计者给出了密封罐的三视图,请你按照三视图确定制作每个密封罐所需钢板的面积.
分析:对于某些立体图形,沿着其中一些线(例如棱柱的棱)剪开,可以把立体图形的表面展开成一个平面图形——展开图.在实际的生产中,三视图和展开图往往结合在一起使用.解决本题的思路是,由三视图想象出密封罐的立体形状,再进一步画出展开图,从而计算面积.
100
50
50
100
典型例题
当堂检测
学习目标
课堂总结
知识梳理
解:由三视图可知,密封罐的现状是正六棱柱.
密封罐的高为50mm,店面正六边形的直径为100mm,边长为50mm,图是它的展开图.
由展开图可知,制作一个密封罐所需钢板的面积为
(mm2)
典型例题
当堂检测
学习目标
课堂总结
知识梳理
5.我国古代数学著作《九章算术》中,将底面是直角三角形,且侧棱与底面垂直的三棱柱称为“堑堵”.某“堑堵”的三视图如图所示(网格图中每个小正方形的边长均为1),则该“堑堵”的侧面积为( )
A. B.
C. D.
A
典型例题
当堂检测
学习目标
课堂总结
知识梳理
中心投影
视图与投影
视图
投影
平行投影
灯光与影子,视点、视线和盲区
圆柱、圆锥、球、直三棱柱、直四棱柱等简单几何体的三视图
