第三十一章 随机事件的概率复习课课件 26张PPT 2023-2024学年冀教版九年级数学下册
文档属性
| 名称 | 第三十一章 随机事件的概率复习课课件 26张PPT 2023-2024学年冀教版九年级数学下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-27 09:58:09 | ||
图片预览








文档简介
(共26张PPT)
第三十一章 随机事件的概率
复习课
典型例题
当堂检测
学习目标
课堂总结
知识梳理
1.掌握必然事件、不可能事件、随机事件的概念
2.能用大量重复试验来计算频率,并用频率估计概率
3.能计算等可能事件的概率,会用概率的大小判断游戏的公平性
4.会用列举法(直接列举、列表法、树状图)求简单事件的概率
1. :在一定条件下,进行重复试验时,有些事情我们事先肯定它一定发生,发生的概率为 .
2. :在一定条件下,进行重复试验时,有些事情我们事先肯定它一定不发生,发生的概率为 .
3. :在一定条件下,进行重复试验时,有些事情我们事先无法肯定它会不会发生,发生的概率在 之间.
必然事件
不可能事件
随机事件
0
1
0~1
典型例题
当堂检测
学习目标
课堂总结
知识梳理
1
确定事件和随机事件
典型例题
当堂检测
学习目标
课堂总结
知识梳理
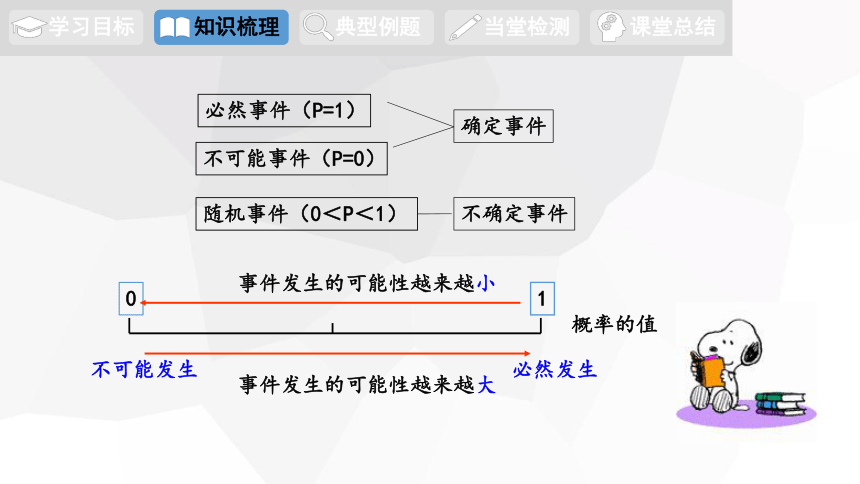
必然事件(P=1)
随机事件(0<P<1)
不可能事件(P=0)
确定事件
不确定事件
0
1
事件发生的可能性越来越大
事件发生的可能性越来越小
不可能发生
必然发生
概率的值
例1.判断下列成语属于哪一类事件.
(1)水涨船高 (2)守株待兔 (3)瓮中捉鳖
(4)水中捞月 (5)缘木求鱼 (6)拔苗助长
解析:必然事件:(1)(3);
随机事件:(2);
不可能事件:(4)(5)(6).
小贴士:把握住必然事件一定发生,不可能事件一定不发生,随机事件的概率在0~1之间即可!
典型例题
当堂检测
学习目标
课堂总结
知识梳理
1.下列说法中,正确的是 ( )
A.不可能事件发生的概率为O
B.随机事件发生的概率为
C.概率很小的事件不可能发生
D.投掷一枚质地均匀的硬币100次,正面朝上的次数一定为50次
A
典型例题
当堂检测
学习目标
课堂总结
知识梳理
2.下列说法正确的是 ( )
A.“任意画出一个等边三角形,它是轴对称图象”是随机事件
B. 任意掷一枚质地均匀的硬币10次,正面向上的一定有5次
C.“概率为0.000 1的事件”是不可能事件
D.“在操场上向上抛出的篮球一定会下落”是确定事件
D
典型例题
当堂检测
学习目标
课堂总结
知识梳理
1.如果随机事件所有可能出现的结果数是m,其中事件A出现的结果数是n,那么事件A发生的概率为P(A)= ,即P(A)= (0≤P≤1).
事件A可能出现的结果
所有可能出现的结果
2.判断游戏规则的公平性:要保证游戏公正合理,就要使规则对玩游戏的双方获胜的概率是 .
相等的
典型例题
当堂检测
学习目标
课堂总结
知识梳理
2
随机事件的概率
(1)几何概率的计算:几何概率模型中概率的大小与面积的大小有关,事件发生的概率等于此事件的可能性结果所组成的图形的面积除以所有可能结果组成图形的面积.
(2)几何概率模型的基本类型:方格中的几何概率与转盘上的几何概率.
3.几何概率的计算:
典型例题
当堂检测
学习目标
课堂总结
知识梳理
例2.小华用如图的转盘设计了一个游戏:指到红色、甲胜;指到黄色,乙胜,他认为转盘有2种颜色,转出每种颜色的可能性都一样,所以游戏公平.
你认可小华的说法吗 这个游戏是否公平?为什么
典型例题
当堂检测
学习目标
课堂总结
知识梳理
解:不认同小华的看法;
因为他没注意到红色部分和黄色部分的面积不相等.
指到红色的概率是 ,指到黄色的概率为 ,∴游戏不公平.
典型例题
当堂检测
学习目标
课堂总结
知识梳理
3.如图是12个大小相同的小正方形,其中5个小正方形已涂上阴影,现随机丢一粒豆子在这12个小正方形内,则它落在阴影部分的概率是( )
A. B. C. D.
B
典型例题
当堂检测
学习目标
课堂总结
知识梳理
4.如图所示,在一个大的圆形区域内包含一个小的圆形区域,大圆的半径为2,小圆的半径为1.如果一只在天空自由飞翔的小鸟要落在图示区域,那么这只小鸟落在小圆形区域外大圆形区域内(阴影部分)的概率是_________.
典型例题
当堂检测
学习目标
课堂总结
知识梳理
5.如图所示的正三角形区域内投针(区域中每个小正三角形除颜色外完全相同),针随机落在某个正三角形内(边线忽略不计)
(1)投针一次,针落在图中阴影区域的概率是多少?
(2)要使针落在图中阴影区域和空白区域的概率均为 ,还要涂黑几个小正三角形?请在图中画出.
解:(1)因为阴影部分的面积与三角形的面积的比值是 ,
所以投针一次击中阴影区域的概率等于 .
(2)2个,如图所示:
典型例题
当堂检测
学习目标
课堂总结
知识梳理
1.在n次重复试验中,随机事件A发生了m次,则称 为事件A发生的频率.
2.在试验次数很大时,事件A发生的频率会在一个常数附近摆动,
这就是 ,可用该值估计事件A发生的概率.
频率的稳定性
典型例题
当堂检测
学习目标
课堂总结
知识梳理
3
用频率估计概率
例3.一个不透明袋子中装有若干个除颜色外均相同的小球,小明每次从袋子中摸出一个球,记录下颜色,然后放回,重复这样的试验1000次,记录结果如下:
实验次数n 200 300 400 500 600 700 800 1000
摸到红球次数m 151 221 289 358 429 497 571 702
摸到红球频率 0.75 0.74 0.72 0.72 0.72 0.71 a b
(1)表格中a= ,b= ;(精确到0.01)
0.71
0.70
典型例题
当堂检测
学习目标
课堂总结
知识梳理
实验次数n 200 300 400 500 600 700 800 1000
摸到红球次数m 151 221 289 358 429 497 571 702
摸到红球频率 0.75 0.74 0.72 0.72 0.72 0.71 a b
(2)估计从袋子中摸出一个球恰好是红球的概率约为 ;(精确到0.1)
(3)若袋子中共有10个球,则除了红球,估计还有 个其他颜色的球.
0.7
3
方法小结:利用频率估计概率会随实验次数的增多,估计值越来越精确,从而可利用表中最后一个频率估计概率
典型例题
当堂检测
学习目标
课堂总结
知识梳理
6.元旦那天,某超市设立了一个如图所示的可以自由转动的转盘,开展有奖购买的活动,顾客购买物品就能获得一次转动转盘的机会,当转盘停止时,就可以获得指针所在区域相对应的奖品.下表是该活动的一组统计数据.假如你去转动一次转盘,获得铅笔的概率大约是 .(精确至0.1)
转动转盘的次数n 100 150 200 500 800 1000
落在“铅笔”区域的次数m 68 108 140 355 560 700
落在“铅笔”区域的频率 0.68 0.72 0.70 0.71 0.70 0.70
0.7
典型例题
当堂检测
学习目标
课堂总结
知识梳理
典型例题
当堂检测
学习目标
课堂总结
知识梳理
4
用列举法求简单事件的概率
1.列表法:当一次试验要涉及两个因素,并且可能出现的结果数目较多时,为了不重不漏的列出所有可能的结果,通常采用列表法.
一个因素所包含的可能情况
另一个因素所包含的可能情况
两个因素所组合的所有可能情况,即n
说明:如果第一个因素包含2种情况;第二个因素包含3种情况;那么所有情况n=2×3=6.
典型例题
当堂检测
学习目标
课堂总结
知识梳理
2.树状图:
树状图的画法
一个试验
第一个因素
第二个因素
如一个试验中涉及2个因数,第一个因数中有2种可能情况;第二个因数中有3种可能的情况.
A
B
1
2
3
1
2
3
则其树形图如图.
n=2×3=6
画树状图法:按事件发生的次序,列出事件可能出现的结果.
典型例题
当堂检测
学习目标
课堂总结
知识梳理
例4.现有A、B、C三盘包子,已知A盘中有两个酸菜包和一个糖包,B盘中有一个酸菜包和一个糖包和一个韭菜包,C盘中有一个酸菜包和一个糖包以及一个馒头.老师就爱吃酸菜包,如果老师从每个盘中各选一个包子(馒头除外),你觉得什么方法求“选的包子全部是酸菜包”的概率更合适,并求出概率是多少?
A
B
C
典型例题
当堂检测
学习目标
课堂总结
知识梳理
解:根据题意,画树状图较为合适,如下:
由树状图得,所有可能出现的结果有18个,它们出现的可能性相等.选的包子全部是酸菜包有2个,所以选的包子全部是酸菜包的概率P=
A盘
B盘
C盘
酸
酸
糖
韭
酸
糖
酸
糖
酸
糖
酸
酸
糖
韭
酸
糖
酸
糖
酸
糖
糖
酸
糖
韭
酸
糖
酸
糖
酸
糖
酸
酸
酸
酸
酸
糖
酸
糖
酸
酸
糖
糖
酸
韭
酸
酸
韭
糖
酸
酸
酸
酸
酸
糖
酸
糖
酸
酸
糖
糖
酸
韭
酸
酸
韭
糖
糖
酸
酸
糖
酸
糖
糖
糖
酸
糖
糖
糖
糖
韭
酸
糖
韭
糖
典型例题
当堂检测
学习目标
课堂总结
知识梳理
7.在一个不透明的袋子里装有四个小球,球上分别标有6,7,8,9四个数字,这些小球除数字外都相同.甲、乙两人玩“猜数字”游戏,甲先从袋中任意摸出一个小球,将小球上的数字记为m,再由乙猜这个小球上的数字,记为n.如果m,n满足|m-n|≤1,那么就称甲、乙两人“心领神会”,则两人“心领神会”的概率是( )
A. B. C. D.
B
典型例题
当堂检测
学习目标
课堂总结
知识梳理
8.在一个不透明的口袋里分别标注2、4、6的3个小球(小球除数字外,其余都相同),另有3张背面完全一样,正面分别写有数字6、7、8的卡片.现从口袋中任意摸出一个小球,再从这3张背面朝上的卡片中任意摸出一张卡片.
(1)请你用列表或画树状图的方法,表示出所有可能出现的结果;
解:(1)列表如下
6 7 8
2 (2,6) (2,7) (2,8)
4 (4,6) (4,7) (4,8)
6 (6,6) (6,7) (6,8)
卡片
小球
共有9种等可能结果;
典型例题
当堂检测
学习目标
课堂总结
知识梳理
(2)小红和小莉做游戏,制定了两个游戏规则:
规则1:若两次摸出的数字,至少有一次是“6”,小红赢;否则,小莉赢;
规则2:若摸出的卡片上的数字是球上数字的整数倍时,小红赢;否则,小莉赢.小红想要在游戏中获胜,她会选择哪一条规则,并说明理由.
解:规则1:P(小红赢)= ;
规则2:P(小红赢)=
∵ , ∴小红选择规则1.
典型例题
当堂检测
学习目标
课堂总结
知识梳理
随机事件
确定性事件
用列举法求概率
用频率估计概率
树状图法
列表法
不可能事件
必然事件
概率的概念
事件
第三十一章 随机事件的概率
复习课
典型例题
当堂检测
学习目标
课堂总结
知识梳理
1.掌握必然事件、不可能事件、随机事件的概念
2.能用大量重复试验来计算频率,并用频率估计概率
3.能计算等可能事件的概率,会用概率的大小判断游戏的公平性
4.会用列举法(直接列举、列表法、树状图)求简单事件的概率
1. :在一定条件下,进行重复试验时,有些事情我们事先肯定它一定发生,发生的概率为 .
2. :在一定条件下,进行重复试验时,有些事情我们事先肯定它一定不发生,发生的概率为 .
3. :在一定条件下,进行重复试验时,有些事情我们事先无法肯定它会不会发生,发生的概率在 之间.
必然事件
不可能事件
随机事件
0
1
0~1
典型例题
当堂检测
学习目标
课堂总结
知识梳理
1
确定事件和随机事件
典型例题
当堂检测
学习目标
课堂总结
知识梳理
必然事件(P=1)
随机事件(0<P<1)
不可能事件(P=0)
确定事件
不确定事件
0
1
事件发生的可能性越来越大
事件发生的可能性越来越小
不可能发生
必然发生
概率的值
例1.判断下列成语属于哪一类事件.
(1)水涨船高 (2)守株待兔 (3)瓮中捉鳖
(4)水中捞月 (5)缘木求鱼 (6)拔苗助长
解析:必然事件:(1)(3);
随机事件:(2);
不可能事件:(4)(5)(6).
小贴士:把握住必然事件一定发生,不可能事件一定不发生,随机事件的概率在0~1之间即可!
典型例题
当堂检测
学习目标
课堂总结
知识梳理
1.下列说法中,正确的是 ( )
A.不可能事件发生的概率为O
B.随机事件发生的概率为
C.概率很小的事件不可能发生
D.投掷一枚质地均匀的硬币100次,正面朝上的次数一定为50次
A
典型例题
当堂检测
学习目标
课堂总结
知识梳理
2.下列说法正确的是 ( )
A.“任意画出一个等边三角形,它是轴对称图象”是随机事件
B. 任意掷一枚质地均匀的硬币10次,正面向上的一定有5次
C.“概率为0.000 1的事件”是不可能事件
D.“在操场上向上抛出的篮球一定会下落”是确定事件
D
典型例题
当堂检测
学习目标
课堂总结
知识梳理
1.如果随机事件所有可能出现的结果数是m,其中事件A出现的结果数是n,那么事件A发生的概率为P(A)= ,即P(A)= (0≤P≤1).
事件A可能出现的结果
所有可能出现的结果
2.判断游戏规则的公平性:要保证游戏公正合理,就要使规则对玩游戏的双方获胜的概率是 .
相等的
典型例题
当堂检测
学习目标
课堂总结
知识梳理
2
随机事件的概率
(1)几何概率的计算:几何概率模型中概率的大小与面积的大小有关,事件发生的概率等于此事件的可能性结果所组成的图形的面积除以所有可能结果组成图形的面积.
(2)几何概率模型的基本类型:方格中的几何概率与转盘上的几何概率.
3.几何概率的计算:
典型例题
当堂检测
学习目标
课堂总结
知识梳理
例2.小华用如图的转盘设计了一个游戏:指到红色、甲胜;指到黄色,乙胜,他认为转盘有2种颜色,转出每种颜色的可能性都一样,所以游戏公平.
你认可小华的说法吗 这个游戏是否公平?为什么
典型例题
当堂检测
学习目标
课堂总结
知识梳理
解:不认同小华的看法;
因为他没注意到红色部分和黄色部分的面积不相等.
指到红色的概率是 ,指到黄色的概率为 ,∴游戏不公平.
典型例题
当堂检测
学习目标
课堂总结
知识梳理
3.如图是12个大小相同的小正方形,其中5个小正方形已涂上阴影,现随机丢一粒豆子在这12个小正方形内,则它落在阴影部分的概率是( )
A. B. C. D.
B
典型例题
当堂检测
学习目标
课堂总结
知识梳理
4.如图所示,在一个大的圆形区域内包含一个小的圆形区域,大圆的半径为2,小圆的半径为1.如果一只在天空自由飞翔的小鸟要落在图示区域,那么这只小鸟落在小圆形区域外大圆形区域内(阴影部分)的概率是_________.
典型例题
当堂检测
学习目标
课堂总结
知识梳理
5.如图所示的正三角形区域内投针(区域中每个小正三角形除颜色外完全相同),针随机落在某个正三角形内(边线忽略不计)
(1)投针一次,针落在图中阴影区域的概率是多少?
(2)要使针落在图中阴影区域和空白区域的概率均为 ,还要涂黑几个小正三角形?请在图中画出.
解:(1)因为阴影部分的面积与三角形的面积的比值是 ,
所以投针一次击中阴影区域的概率等于 .
(2)2个,如图所示:
典型例题
当堂检测
学习目标
课堂总结
知识梳理
1.在n次重复试验中,随机事件A发生了m次,则称 为事件A发生的频率.
2.在试验次数很大时,事件A发生的频率会在一个常数附近摆动,
这就是 ,可用该值估计事件A发生的概率.
频率的稳定性
典型例题
当堂检测
学习目标
课堂总结
知识梳理
3
用频率估计概率
例3.一个不透明袋子中装有若干个除颜色外均相同的小球,小明每次从袋子中摸出一个球,记录下颜色,然后放回,重复这样的试验1000次,记录结果如下:
实验次数n 200 300 400 500 600 700 800 1000
摸到红球次数m 151 221 289 358 429 497 571 702
摸到红球频率 0.75 0.74 0.72 0.72 0.72 0.71 a b
(1)表格中a= ,b= ;(精确到0.01)
0.71
0.70
典型例题
当堂检测
学习目标
课堂总结
知识梳理
实验次数n 200 300 400 500 600 700 800 1000
摸到红球次数m 151 221 289 358 429 497 571 702
摸到红球频率 0.75 0.74 0.72 0.72 0.72 0.71 a b
(2)估计从袋子中摸出一个球恰好是红球的概率约为 ;(精确到0.1)
(3)若袋子中共有10个球,则除了红球,估计还有 个其他颜色的球.
0.7
3
方法小结:利用频率估计概率会随实验次数的增多,估计值越来越精确,从而可利用表中最后一个频率估计概率
典型例题
当堂检测
学习目标
课堂总结
知识梳理
6.元旦那天,某超市设立了一个如图所示的可以自由转动的转盘,开展有奖购买的活动,顾客购买物品就能获得一次转动转盘的机会,当转盘停止时,就可以获得指针所在区域相对应的奖品.下表是该活动的一组统计数据.假如你去转动一次转盘,获得铅笔的概率大约是 .(精确至0.1)
转动转盘的次数n 100 150 200 500 800 1000
落在“铅笔”区域的次数m 68 108 140 355 560 700
落在“铅笔”区域的频率 0.68 0.72 0.70 0.71 0.70 0.70
0.7
典型例题
当堂检测
学习目标
课堂总结
知识梳理
典型例题
当堂检测
学习目标
课堂总结
知识梳理
4
用列举法求简单事件的概率
1.列表法:当一次试验要涉及两个因素,并且可能出现的结果数目较多时,为了不重不漏的列出所有可能的结果,通常采用列表法.
一个因素所包含的可能情况
另一个因素所包含的可能情况
两个因素所组合的所有可能情况,即n
说明:如果第一个因素包含2种情况;第二个因素包含3种情况;那么所有情况n=2×3=6.
典型例题
当堂检测
学习目标
课堂总结
知识梳理
2.树状图:
树状图的画法
一个试验
第一个因素
第二个因素
如一个试验中涉及2个因数,第一个因数中有2种可能情况;第二个因数中有3种可能的情况.
A
B
1
2
3
1
2
3
则其树形图如图.
n=2×3=6
画树状图法:按事件发生的次序,列出事件可能出现的结果.
典型例题
当堂检测
学习目标
课堂总结
知识梳理
例4.现有A、B、C三盘包子,已知A盘中有两个酸菜包和一个糖包,B盘中有一个酸菜包和一个糖包和一个韭菜包,C盘中有一个酸菜包和一个糖包以及一个馒头.老师就爱吃酸菜包,如果老师从每个盘中各选一个包子(馒头除外),你觉得什么方法求“选的包子全部是酸菜包”的概率更合适,并求出概率是多少?
A
B
C
典型例题
当堂检测
学习目标
课堂总结
知识梳理
解:根据题意,画树状图较为合适,如下:
由树状图得,所有可能出现的结果有18个,它们出现的可能性相等.选的包子全部是酸菜包有2个,所以选的包子全部是酸菜包的概率P=
A盘
B盘
C盘
酸
酸
糖
韭
酸
糖
酸
糖
酸
糖
酸
酸
糖
韭
酸
糖
酸
糖
酸
糖
糖
酸
糖
韭
酸
糖
酸
糖
酸
糖
酸
酸
酸
酸
酸
糖
酸
糖
酸
酸
糖
糖
酸
韭
酸
酸
韭
糖
酸
酸
酸
酸
酸
糖
酸
糖
酸
酸
糖
糖
酸
韭
酸
酸
韭
糖
糖
酸
酸
糖
酸
糖
糖
糖
酸
糖
糖
糖
糖
韭
酸
糖
韭
糖
典型例题
当堂检测
学习目标
课堂总结
知识梳理
7.在一个不透明的袋子里装有四个小球,球上分别标有6,7,8,9四个数字,这些小球除数字外都相同.甲、乙两人玩“猜数字”游戏,甲先从袋中任意摸出一个小球,将小球上的数字记为m,再由乙猜这个小球上的数字,记为n.如果m,n满足|m-n|≤1,那么就称甲、乙两人“心领神会”,则两人“心领神会”的概率是( )
A. B. C. D.
B
典型例题
当堂检测
学习目标
课堂总结
知识梳理
8.在一个不透明的口袋里分别标注2、4、6的3个小球(小球除数字外,其余都相同),另有3张背面完全一样,正面分别写有数字6、7、8的卡片.现从口袋中任意摸出一个小球,再从这3张背面朝上的卡片中任意摸出一张卡片.
(1)请你用列表或画树状图的方法,表示出所有可能出现的结果;
解:(1)列表如下
6 7 8
2 (2,6) (2,7) (2,8)
4 (4,6) (4,7) (4,8)
6 (6,6) (6,7) (6,8)
卡片
小球
共有9种等可能结果;
典型例题
当堂检测
学习目标
课堂总结
知识梳理
(2)小红和小莉做游戏,制定了两个游戏规则:
规则1:若两次摸出的数字,至少有一次是“6”,小红赢;否则,小莉赢;
规则2:若摸出的卡片上的数字是球上数字的整数倍时,小红赢;否则,小莉赢.小红想要在游戏中获胜,她会选择哪一条规则,并说明理由.
解:规则1:P(小红赢)= ;
规则2:P(小红赢)=
∵ , ∴小红选择规则1.
典型例题
当堂检测
学习目标
课堂总结
知识梳理
随机事件
确定性事件
用列举法求概率
用频率估计概率
树状图法
列表法
不可能事件
必然事件
概率的概念
事件
