用二分法求方程的近似解
图片预览





文档简介
(共14张PPT)
用二分法求方程的近似解
怀化市铁路第一中学高一数学备课组
一、复习引入
1、函数零点存在性定理
如果函数y=f(x)在区间[a, b]上的图象是一条连续不断的曲线, 并且有f(a) ·f(b) <0, 那么函数y=f(x)在区间(a, b)内有零点, 即存在c∈ (a, b), 使得f(c)=0, 这个c也就是方程f(x)=0的根.
闭端反连,开内零点.
让你来猜这款手机的价格,你如何猜
逐步逼近
猜价格, 送手机!!!
我们能否采用这种逐步逼近的方法来解决一些数学问题呢?
问题、求解方程 x2-2x-1=0
方法一:用求根公式可得:
二、知识探究
不用求根公式,如何用这种逐步逼近的方法来求方程的近似解?
方程x2-2x-1=0的解, 也就是函数y=x2-2x-1的图象与x轴交点的横坐标 (函数的零点).
y
x
0
3
2
1
-1
y=x2-2x-1
x1
x2
函数y=x2-2x-1的图象如下 :
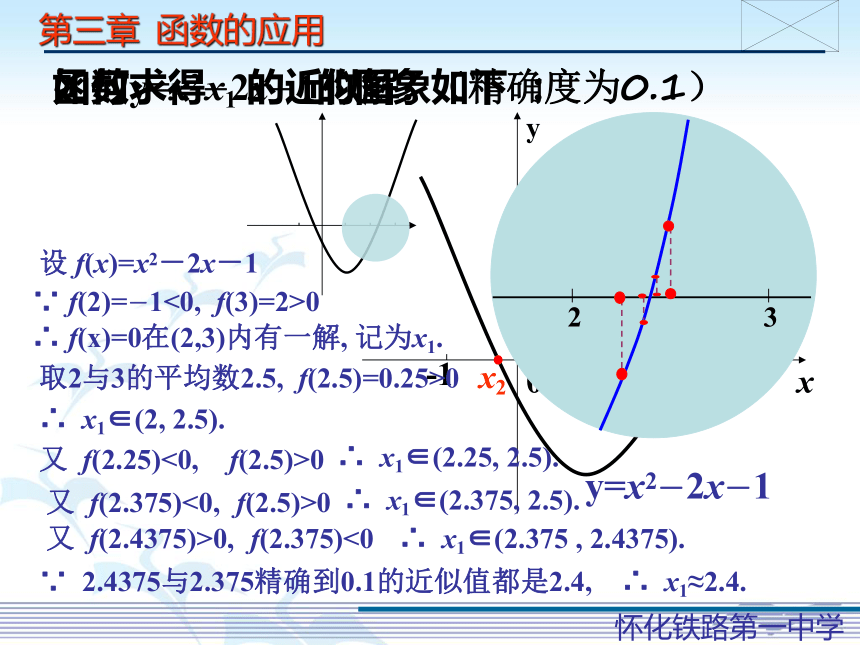
如何求得x1 的近似解 (精确度为0.1)
2
3
设 f(x)=x2-2x-1
∵ f(2)=-1<0, f(3)=2>0
∴ f(x)=0在(2,3)内有一解, 记为x1.
取2与3的平均数2.5, f(2.5)=0.25>0
∴ x1∈(2, 2.5).
又 f(2.25)<0,
f(2.5)>0
∴ x1∈(2.25, 2.5).
又 f(2.375)<0,
f(2.5)>0
∴ x1∈(2.375, 2.5).
又 f(2.4375)>0,
f(2.375)<0
∴ x1∈(2.375 , 2.4375).
∵ 2.4375与2.375精确到0.1的近似值都是2.4,
∴ x1≈2.4.
对于在区间[a, b]上连续不断、且 f(a) · f(b)<0的函数y=f(x)通过不断地把函数的零点所在的区间一分为二,使区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫做二分法.
三、二分法
1. 能使用二分法的条件:
连续不断、且 f(a) · f(b)<0
2. 使用二分法的要点:
一分为二→逐步逼近→得到零点近似值
闭端反连
折半逼近
二分法求解方程近似解的基本步骤
2. 求区间[a, b]的中点 .
1. 用估算或作图的方法, 确定初始区间[a, b], 使 f(a) · f(b)<0, 给定精确度ε.
3. 计算 f(c).
⑴. 若 f(c)=0, 则c是函数的零点.
⑵. 若 f(a)· f(c)< 0, 则令b=c(此时零点x0∈(a, c).
⑶. 若 f(b)· f(c)< 0, 则令a=c(此时零点x0∈(c, b).
4. 判断是否达到精确度ε, 即若|a-b|<ε, 则得到零点近似值a或b, 否则重复2~4.
例 利用计算器,求方程 lgx=3-x的近似解(精确度0.1).
如图:分别画两个函数的图形?
从图形中你能发现什么
x
1
2
3
4
0
y
3
原方程与
有何关系
四、知识运用
想一想
如何确定初始区间(a,b)
估算或作图
x0
x0∈(2, 3)
有唯一解x0, 且
解:设 f(x)=lgx+x-3,
设函数的零点为x0, 用计算器算得:
∴ 原方程的近似解为 x0≈2.6.
五、课堂练习
1. 下列图象的函数中,不能用二分法求零点的是( )
B
2. 在26枚崭新的钻石中, 混入了一枚外表和它们完全相同的假钻石(重量轻一点), 现在有一台天平, 请问你最多称 次就可以发现这枚假钻石.
4
3. 根据下表中的数据, 可以判定方程ex-x-2=0的一个
根所在的区间为( )
x - 1 0 1 2 3
ex 0.37 1 2.72 7.39 20.0
x+2 1 2 3 4 5
A. (-1, 0) B.(0, 1) C. (1, 2) D. (2, 3)
C
六、课堂小结
1. 用二分法求方程的近似解
2. 二分法的算法特点:
闭端反连,折半逼近.
——是一种通法,体现了逐步逼近的数学思想,
只要按部就班地去做,总会算出结果.
——是刻板的、机械的,进行大量的重复计算,
——在现代条件下,大量的计算可以让计算机来
完成.
THE END
再见!
用二分法求方程的近似解
怀化市铁路第一中学高一数学备课组
一、复习引入
1、函数零点存在性定理
如果函数y=f(x)在区间[a, b]上的图象是一条连续不断的曲线, 并且有f(a) ·f(b) <0, 那么函数y=f(x)在区间(a, b)内有零点, 即存在c∈ (a, b), 使得f(c)=0, 这个c也就是方程f(x)=0的根.
闭端反连,开内零点.
让你来猜这款手机的价格,你如何猜
逐步逼近
猜价格, 送手机!!!
我们能否采用这种逐步逼近的方法来解决一些数学问题呢?
问题、求解方程 x2-2x-1=0
方法一:用求根公式可得:
二、知识探究
不用求根公式,如何用这种逐步逼近的方法来求方程的近似解?
方程x2-2x-1=0的解, 也就是函数y=x2-2x-1的图象与x轴交点的横坐标 (函数的零点).
y
x
0
3
2
1
-1
y=x2-2x-1
x1
x2
函数y=x2-2x-1的图象如下 :
如何求得x1 的近似解 (精确度为0.1)
2
3
设 f(x)=x2-2x-1
∵ f(2)=-1<0, f(3)=2>0
∴ f(x)=0在(2,3)内有一解, 记为x1.
取2与3的平均数2.5, f(2.5)=0.25>0
∴ x1∈(2, 2.5).
又 f(2.25)<0,
f(2.5)>0
∴ x1∈(2.25, 2.5).
又 f(2.375)<0,
f(2.5)>0
∴ x1∈(2.375, 2.5).
又 f(2.4375)>0,
f(2.375)<0
∴ x1∈(2.375 , 2.4375).
∵ 2.4375与2.375精确到0.1的近似值都是2.4,
∴ x1≈2.4.
对于在区间[a, b]上连续不断、且 f(a) · f(b)<0的函数y=f(x)通过不断地把函数的零点所在的区间一分为二,使区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫做二分法.
三、二分法
1. 能使用二分法的条件:
连续不断、且 f(a) · f(b)<0
2. 使用二分法的要点:
一分为二→逐步逼近→得到零点近似值
闭端反连
折半逼近
二分法求解方程近似解的基本步骤
2. 求区间[a, b]的中点 .
1. 用估算或作图的方法, 确定初始区间[a, b], 使 f(a) · f(b)<0, 给定精确度ε.
3. 计算 f(c).
⑴. 若 f(c)=0, 则c是函数的零点.
⑵. 若 f(a)· f(c)< 0, 则令b=c(此时零点x0∈(a, c).
⑶. 若 f(b)· f(c)< 0, 则令a=c(此时零点x0∈(c, b).
4. 判断是否达到精确度ε, 即若|a-b|<ε, 则得到零点近似值a或b, 否则重复2~4.
例 利用计算器,求方程 lgx=3-x的近似解(精确度0.1).
如图:分别画两个函数的图形?
从图形中你能发现什么
x
1
2
3
4
0
y
3
原方程与
有何关系
四、知识运用
想一想
如何确定初始区间(a,b)
估算或作图
x0
x0∈(2, 3)
有唯一解x0, 且
解:设 f(x)=lgx+x-3,
设函数的零点为x0, 用计算器算得:
∴ 原方程的近似解为 x0≈2.6.
五、课堂练习
1. 下列图象的函数中,不能用二分法求零点的是( )
B
2. 在26枚崭新的钻石中, 混入了一枚外表和它们完全相同的假钻石(重量轻一点), 现在有一台天平, 请问你最多称 次就可以发现这枚假钻石.
4
3. 根据下表中的数据, 可以判定方程ex-x-2=0的一个
根所在的区间为( )
x - 1 0 1 2 3
ex 0.37 1 2.72 7.39 20.0
x+2 1 2 3 4 5
A. (-1, 0) B.(0, 1) C. (1, 2) D. (2, 3)
C
六、课堂小结
1. 用二分法求方程的近似解
2. 二分法的算法特点:
闭端反连,折半逼近.
——是一种通法,体现了逐步逼近的数学思想,
只要按部就班地去做,总会算出结果.
——是刻板的、机械的,进行大量的重复计算,
——在现代条件下,大量的计算可以让计算机来
完成.
THE END
再见!
