江苏省江阴市青阳片2023-2024学年九年级上学期12月作业检查数学试卷(含答案)
文档属性
| 名称 | 江苏省江阴市青阳片2023-2024学年九年级上学期12月作业检查数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 401.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-27 09:55:01 | ||
图片预览


文档简介
2023-2024学年第一学期初三数学12月份作业检查试卷
(满分150 时间120分钟)
一、选择题(本大题共有10小题,每小题3分,共30分,在每小题所给出的四个选项中,只有一项是正确的,请把正确选项前的字母代号填在题后的括号内)
1.tan45°的值等于( )
A. B. C.1 D.
2.下列函数中一定是二次函数的是( )
A.y=3x﹣1 B.y=ax2+bx+c
C.y=x2+ D.s=2t2﹣2t+1
3.如图,CD为⊙O的直径,弦AB⊥CD于E,OE=12,AB=10,那么直径CD的长为( )
A.12.5 B.13 C.25 D.26
4.Rt△ABC中,∠C=90°,AC=1,BC=2,tanA的值为( )
A. B. C. D.2
5.下列说法正确的是( )
A.三点确定一个圆
B.任何三角形有且只有一个内切圆
C.长度相等的弧是等弧
D.三角形的外心是三条角平分线的交点
6.已知△ABC∽△DEF,相似比为1:2,且△ABC的周长为18,则△DEF的周长为( )
A.9 B.36 C.4.5 D.72
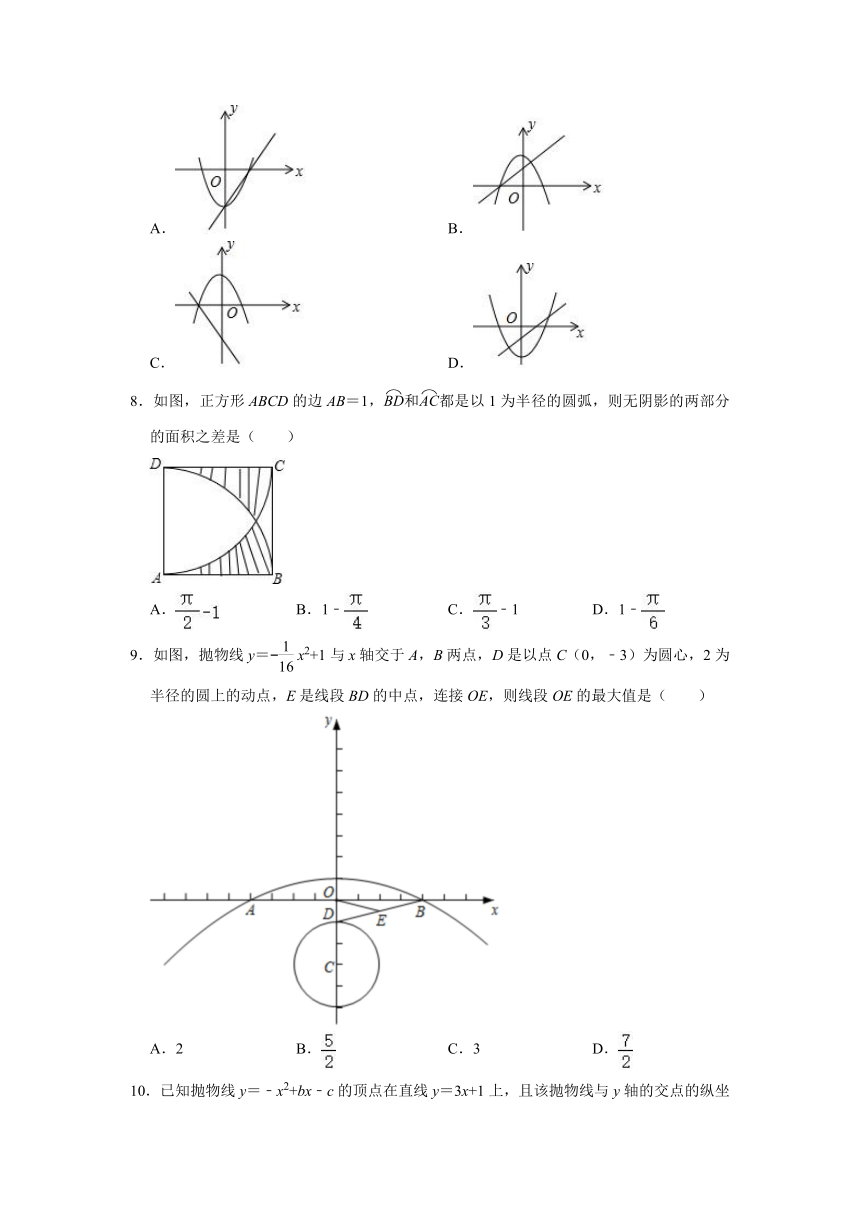
7.函数y=ax2﹣a与y=ax+a(a≠0)在同一坐标系中的图象可能是( )
A. B.
C. D.
8.如图,正方形ABCD的边AB=1,和都是以1为半径的圆弧,则无阴影的两部分的面积之差是( )
A. B.1﹣ C.﹣1 D.1﹣
9.如图,抛物线y= x2+1与x轴交于A,B两点,D是以点C(0,﹣3)为圆心,2为半径的圆上的动点,E是线段BD的中点,连接OE,则线段OE的最大值是( )
A.2 B. C.3 D.
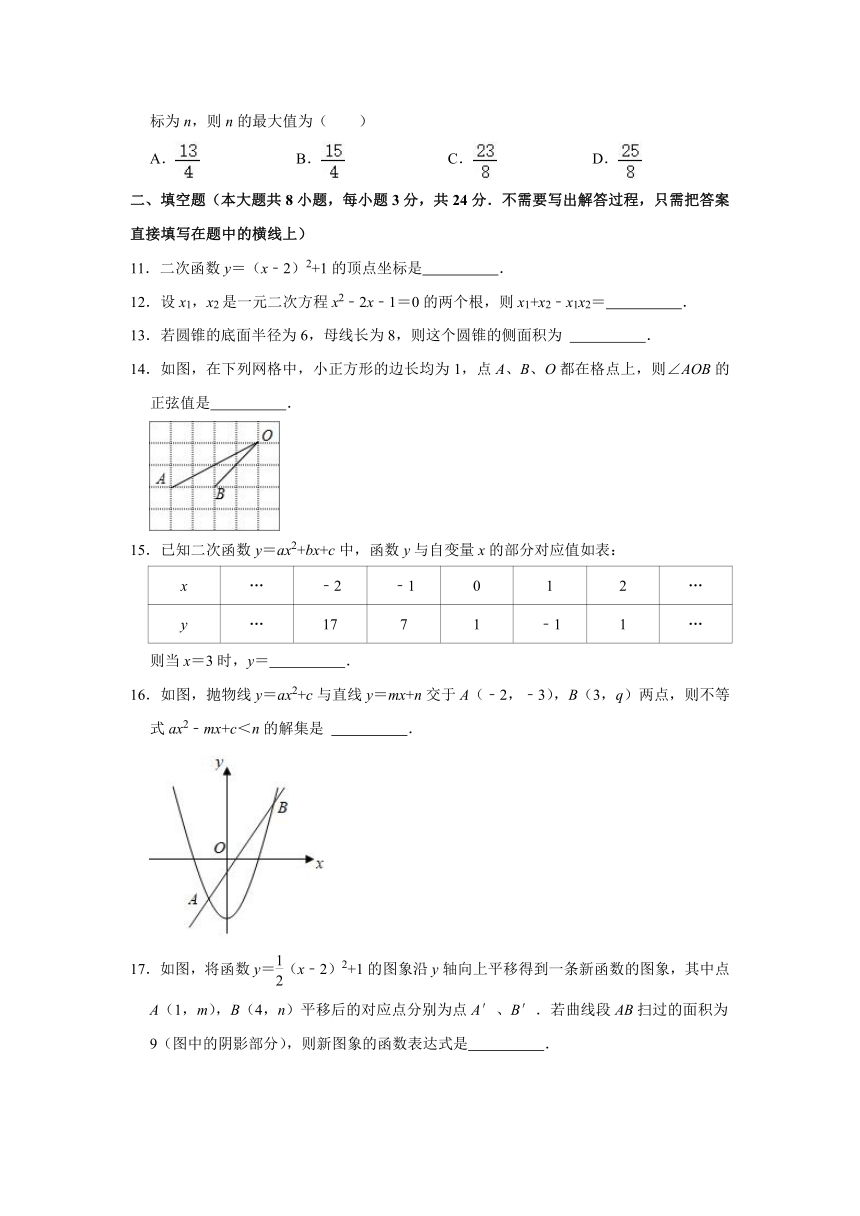
10.已知抛物线y=﹣x2+bx﹣c的顶点在直线y=3x+1上,且该抛物线与y轴的交点的纵坐标为n,则n的最大值为( )
A. B. C. D.
二、填空题(本大题共8小题,每小题3分,共24分.不需要写出解答过程,只需把答案直接填写在题中的横线上)
11.二次函数y=(x﹣2)2+1的顶点坐标是 .
12.设x1,x2是一元二次方程x2﹣2x﹣1=0的两个根,则x1+x2﹣x1x2= .
13.若圆锥的底面半径为6,母线长为8,则这个圆锥的侧面积为 .
14.如图,在下列网格中,小正方形的边长均为1,点A、B、O都在格点上,则∠AOB的正弦值是 .
15.已知二次函数y=ax2+bx+c中,函数y与自变量x的部分对应值如表:
x … ﹣2 ﹣1 0 1 2 …
y … 17 7 1 ﹣1 1 …
则当x=3时,y= .
16.如图,抛物线y=ax2+c与直线y=mx+n交于A(﹣2,﹣3),B(3,q)两点,则不等式ax2﹣mx+c<n的解集是 .
17.如图,将函数y=(x﹣2)2+1的图象沿y轴向上平移得到一条新函数的图象,其中点A(1,m),B(4,n)平移后的对应点分别为点A′、B′.若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是 .
18.如图,在平面直角坐标系中,点A(0,4),弧MN所在圆的圆心在x轴上,其中M(0,3),N(4,5),点P为弧MN上一点,则线段AP长度的最小值为 .
三、解答题(本大题共10小题,共96分,解答时应写出文字说明、证明过程或演算步骤)
19.(8分)解方程:
(1)(x﹣1)2﹣25=0 (2)x2﹣4x﹣1=0
20.(8分)解方程:计算:
(1) (2)cos45°﹣tan260°﹣|sin45°﹣1|
21.(10分)如图,平面直角坐标系中,A点坐标(1,0),B点坐标(4,1),C点坐标(6,5),请按要求用无刻度直尺在格点图上完成下列作图.
(1)以点A为位似中心,位似比为2:1,将△ABC放大得到△ADE;
(2)△ADE面积为 .
(3)在图中画出△ABC外接圆的圆心P,点P的坐标为 .
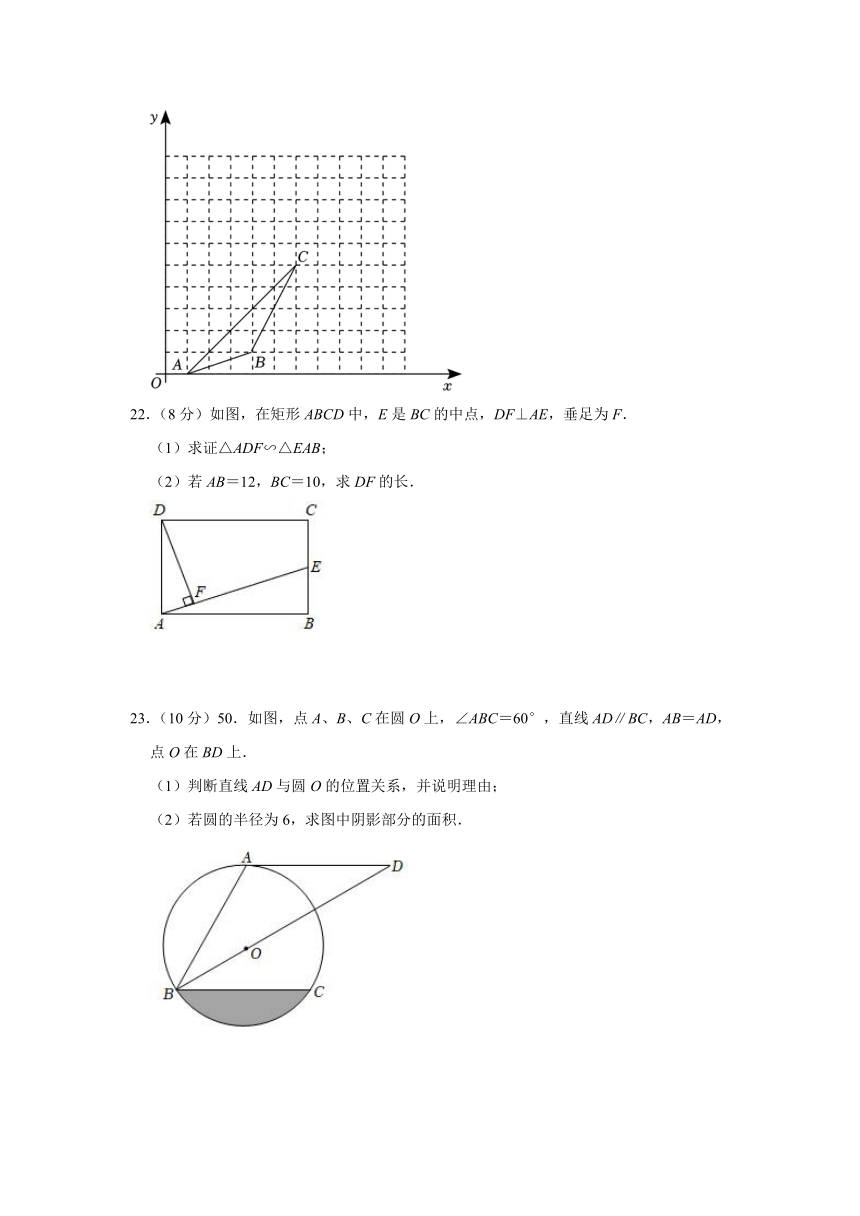
22.(8分)如图,在矩形ABCD中,E是BC的中点,DF⊥AE,垂足为F.
(1)求证△ADF∽△EAB;
(2)若AB=12,BC=10,求DF的长.
23.(10分)50.如图,点A、B、C在圆O上,∠ABC=60°,直线AD∥BC,AB=AD,点O在BD上.
(1)判断直线AD与圆O的位置关系,并说明理由;
(2)若圆的半径为6,求图中阴影部分的面积.
24.(10分)无锡市政府为了方便市民绿色出行,推出了共享单车服务.图①是某品牌共享单车放在水平地面上的实物图,图②是其示意图,其中AB、CD都与地面l平行,车轮半径为32cm,∠BCD=64°,BC=60cm,坐垫E与点B的距离BE为15cm.
(1)求坐垫E到地面的距离;
(2)根据经验,当坐垫E到CD的距离调整为人体腿长的0.8时,坐骑比较舒适.小明的腿长约为80cm,现将坐垫E调整至坐骑舒适高度位置E',求EE′的长.
(结果精确到0.1cm,参考数据:sin64°≈0.90,cos64°≈0.44,tan64°≈2.05)
25.(10分)某商店销售一种进价50元/件的商品,经市场调查发现:该商品的每天销售量y(件)是售价x(元/件)的一次函数,其售价、销售量的二组对应值如下表:
售价x(元/件) 55 65
销售量y(件/天) 90 70
(1)若某天销售利润为800元,求该天的售价为多少元/件?
(2)设该商店销售商品每天获得的利润为W(元),求W与x之间的函数关系式,并求出当销售单价定为多少时,该商店销售这种商品每天获得的利润最大?
26.(10分)【问题提出】如何用圆规和无刻度的直尺作一条直线或圆弧平分已知扇形的面积?
【初步尝试】如图1,已知扇形OAB,请你用圆规和无刻度的直尺过圆心O作一条直线,使扇形的面积被这条直线平分;
【问题联想】如图2,已知线段MN,请你用圆规和无刻度的直尺作一个以MN为斜边的等腰直角三角形MNP;
【问题再解】如图3,已知扇形OAB,请你用圆规和无刻度的直尺作一条以点O为圆心的圆弧,使扇形的面积被这条圆弧平分.
(友情提醒:以上作图均不写作法,但需保留作图痕迹)
27.(10分)如图,在Rt△ABC中,∠C=90°,AB=10cm,AC:BC=4:3,点P从点A出发沿AB方向向点B运动,速度为1cm/s,同时点Q从点B出发沿B→C→A方向向点A运动,速度为2cm/s,当一个运动点到达终点时,另一个运动点也随之停止运动.
(1)AC= cm;BC= cm;
(2)设点P的运动时间为x秒(x>0),△PBQ的面积为y cm2,当△PBQ存在时,求y与x的函数关系式,并写出自变量x的取值范围;
(3)当点Q在BC上运动时,多少秒时△PBQ的面积为15cm2?
28.(12分)如图a,抛物线y=ax2﹣2ax﹣b(a<0)与x轴的一个交点为B(﹣1,0),与y轴的正半轴交于点C,顶点为D.
(1)求顶点D的坐标(用含a的代数式表示);
(2)若以AD为直径的圆经过点C.
①求抛物线的解析式;
②如图b,点E是y轴负半轴上的一点,连接BE,将△OBE绕平面内某一点旋转180°,得到△PMN(点P、M、N分别和点O、B、E对应),并且点M、N都在抛物线上,作MF⊥x轴于点F,若线段MF:BF=1:2,求点M、N的坐标;
③如图c,点Q在抛物线的对称轴上,以Q为圆心的圆过A、B两点,并且和直线CD相切,求点Q的坐标.
2023-2024学年第一学期初三数学12月份作业检查试卷
参考答案
一、选择题(本大题共有10小题,每小题3分,共30分)
1 2 3 4 5 6 7 8 9 10
C D D D B B C A D A
二.填空题(本大题有8小题,每空3分,共24分)
11(2,1) 12. 3 13. 48π 14.
15. 7 16.﹣2<x<3 17.y=(x﹣2)2+4 18. 3
三、解答题(本大题共10小题,共96分,)
19.(8分)解方程:
解:(1)由原方程得:(x﹣1)2=25,
得x﹣1=±5, …………………………(2分)
解得x1=6,x2=﹣4, …………………………(4分)
(2)由原方程得:x2﹣4x=1,
得x2﹣4x+4=1+4,(x﹣2)2=5, …………………………(2分)
得,
解得,, …………………………(4分)
20.(8分)计算:
解:(1)原式= …………………………(2分)
=; …………………………(4分)
(2)原式= …………………………(2分)
=
=. …………………………(4分)
(10分)解:(1)如图1所示,△ADE即为所求;
…………………………(4分)
(2)如图2,
S△ADE=S△AME﹣S△AMD﹣S△EMD
=×10×10﹣×10×2﹣×10×4
=20,
故答案为:20; …………………………(7分)
(3)如图3,找到格点F,G,作BC,AC的垂直平分线DF,PG,交于点P,则点..即为所求,
∴P点的坐标为(1,5).
故答案为:(1,5). …………………………(10分)
22.(8分)(1)证明:∵四边形ABCD是矩形,
∴AD∥BC,∠B=90°,
∴∠DAF=∠AEB, …………………………(2分)
∵DF⊥AE,
∴∠AFD=90°=∠B,
∴△ADF∽△EAB; …………………………(4分)
(2)解:∵BC=AD=10,E是BC边的中点,
∴BE=5,
∴AE===13, …………………………(6分)
由(1)得:△ADF∽△EAB,
∴=,
即=,
解得:DF=. …………………………(4分)
23.(10分)解:(1)直线AD与圆O相切, …………………………(1分)
连接OA,
∵AD∥BC,
∴∠D=∠DBC,
∵AD=AB,
∴∠D=∠ABD,
∴∠DBC=∠ABD=30°, …………………………(3分)
∠BAD=120°,
∵OA=OB,
∴∠BAO=∠ABD=30°, …………………………(4分)
∴∠OAD=90°,
∴OA⊥AD,
∵OA是圆的半径,
∴直线AD与圆O相切, …………………………(5分)
(2)连接OC,作OH⊥BC于H,
∵OB=OC,
∴∠OCB=∠OBC=30°,
∴∠BOC=120°,
∴OH=OB=3,BH=OH=3,
∴BC=2BH=6,
∴扇形OBC的面积为:==12π, …………………………(7分)
∵S△OBC=BC OH=×6×3=9, …………………………(9分)
∴阴影部分的面积为:12π﹣9. …………………………(10分)
24.(10分)解:(1)如图1,过点E作EM⊥CD于点M,
由题意知∠BCM=64°、EC=BC+BE=60+15=75cm, …………………………(2分)
∴EM=ECsin∠BCM=75sin64°≈67.5(cm),
则单车车座E到地面的高度为67.5+32≈99.5(cm); …………………………(5分)
(2)如图2所示,过点E′作E′H⊥CD于点H,
由题意知E′H=80×0.8=64, …………………………(6分)
则E′C==≈71.1(cm), …………………………(8分)
∴EE′=CE﹣CE′=75﹣71.1=3.9(cm). …………………………(10分)
25.(10分)解:(1)依题意设y=kx+b,
则有,
解得:,
∴y=﹣2x+200,
若某天销售利润为800元, …………………………(2分)
则(x﹣50)(﹣2x+200)=800,
解得:x1=60,x2=90, …………………………(4分)
∴该天的售价为60元或者90元; …………………………(5分)
(2)根据题意得,
W=(x﹣50)(﹣2x+200)=﹣2x2+300x﹣10000=﹣2(x﹣75)2+1250,……(7分)
∵a=﹣2<0,
∴当x=75时,W有最大值1250, …………………………(9分)
答:当销售单价定为75元时利润最大 …………………………(10分)
26.(10分)解:【初步尝试】如图1,直线OP即为所求; ……………………(3分)
【问题联想】如图2,三角形MNP即为所求; …………………………(6分)
【问题再解】如图3中,即为所求. …………………………(10分)
27(10分).解:(1)设AC=4x cm,BC=3x cm,
在Rt△ABC中,AC2+BC2=AB2,
得(4x)2+(3x)2=102,
解得x=2(负值舍去),
∴AC=8cm,BC=6cm,
故答案为:8,6; …………………………(2分)
(2)解:如图2:当Q在BC上运动时,过Q作QH⊥AB于点H,
∵AP=x,BQ=2x,
∴PB=10﹣x,
∵∠BHQ=∠BCA=90°,∠QBH=∠ABC,
∴△BQH∽△BAC,
∴,
∴,
解得,
∴;………………(4分)
如图3:当Q在CA上运动时,过Q作QH′⊥AB于点H′,
∵AP=x,B→C→Q的路程为2x,
∴PB=10﹣x,AQ=14﹣2x,
∵∠AH′Q=∠ACB=90°,∠QAH′=∠BAC,
∴△AQH∽△ABC,
∴,
∴,
解得,
∴ …(6分)
综上,y=; …………………………(7分)
(3)解:当点Q在BC上运动时,,
当y=15时,,
解得,(舍去),
故当点Q在BC上运动时,秒时△PBQ的面积为15cm2. ……………………(10分)
28.(12分)解:(1)D(1,﹣4a). …………………………(2分)
(2)①有题设知∠ACD=90°;
a=﹣1,抛物线的解析式为y=﹣x2+2x+3. …………………………(5分)
②点M的坐标为(,);N(,). …………………………(8分)
③点Q(1,﹣4+2)或(1,﹣4﹣2).…………………………(12分)
(满分150 时间120分钟)
一、选择题(本大题共有10小题,每小题3分,共30分,在每小题所给出的四个选项中,只有一项是正确的,请把正确选项前的字母代号填在题后的括号内)
1.tan45°的值等于( )
A. B. C.1 D.
2.下列函数中一定是二次函数的是( )
A.y=3x﹣1 B.y=ax2+bx+c
C.y=x2+ D.s=2t2﹣2t+1
3.如图,CD为⊙O的直径,弦AB⊥CD于E,OE=12,AB=10,那么直径CD的长为( )
A.12.5 B.13 C.25 D.26
4.Rt△ABC中,∠C=90°,AC=1,BC=2,tanA的值为( )
A. B. C. D.2
5.下列说法正确的是( )
A.三点确定一个圆
B.任何三角形有且只有一个内切圆
C.长度相等的弧是等弧
D.三角形的外心是三条角平分线的交点
6.已知△ABC∽△DEF,相似比为1:2,且△ABC的周长为18,则△DEF的周长为( )
A.9 B.36 C.4.5 D.72
7.函数y=ax2﹣a与y=ax+a(a≠0)在同一坐标系中的图象可能是( )
A. B.
C. D.
8.如图,正方形ABCD的边AB=1,和都是以1为半径的圆弧,则无阴影的两部分的面积之差是( )
A. B.1﹣ C.﹣1 D.1﹣
9.如图,抛物线y= x2+1与x轴交于A,B两点,D是以点C(0,﹣3)为圆心,2为半径的圆上的动点,E是线段BD的中点,连接OE,则线段OE的最大值是( )
A.2 B. C.3 D.
10.已知抛物线y=﹣x2+bx﹣c的顶点在直线y=3x+1上,且该抛物线与y轴的交点的纵坐标为n,则n的最大值为( )
A. B. C. D.
二、填空题(本大题共8小题,每小题3分,共24分.不需要写出解答过程,只需把答案直接填写在题中的横线上)
11.二次函数y=(x﹣2)2+1的顶点坐标是 .
12.设x1,x2是一元二次方程x2﹣2x﹣1=0的两个根,则x1+x2﹣x1x2= .
13.若圆锥的底面半径为6,母线长为8,则这个圆锥的侧面积为 .
14.如图,在下列网格中,小正方形的边长均为1,点A、B、O都在格点上,则∠AOB的正弦值是 .
15.已知二次函数y=ax2+bx+c中,函数y与自变量x的部分对应值如表:
x … ﹣2 ﹣1 0 1 2 …
y … 17 7 1 ﹣1 1 …
则当x=3时,y= .
16.如图,抛物线y=ax2+c与直线y=mx+n交于A(﹣2,﹣3),B(3,q)两点,则不等式ax2﹣mx+c<n的解集是 .
17.如图,将函数y=(x﹣2)2+1的图象沿y轴向上平移得到一条新函数的图象,其中点A(1,m),B(4,n)平移后的对应点分别为点A′、B′.若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是 .
18.如图,在平面直角坐标系中,点A(0,4),弧MN所在圆的圆心在x轴上,其中M(0,3),N(4,5),点P为弧MN上一点,则线段AP长度的最小值为 .
三、解答题(本大题共10小题,共96分,解答时应写出文字说明、证明过程或演算步骤)
19.(8分)解方程:
(1)(x﹣1)2﹣25=0 (2)x2﹣4x﹣1=0
20.(8分)解方程:计算:
(1) (2)cos45°﹣tan260°﹣|sin45°﹣1|
21.(10分)如图,平面直角坐标系中,A点坐标(1,0),B点坐标(4,1),C点坐标(6,5),请按要求用无刻度直尺在格点图上完成下列作图.
(1)以点A为位似中心,位似比为2:1,将△ABC放大得到△ADE;
(2)△ADE面积为 .
(3)在图中画出△ABC外接圆的圆心P,点P的坐标为 .
22.(8分)如图,在矩形ABCD中,E是BC的中点,DF⊥AE,垂足为F.
(1)求证△ADF∽△EAB;
(2)若AB=12,BC=10,求DF的长.
23.(10分)50.如图,点A、B、C在圆O上,∠ABC=60°,直线AD∥BC,AB=AD,点O在BD上.
(1)判断直线AD与圆O的位置关系,并说明理由;
(2)若圆的半径为6,求图中阴影部分的面积.
24.(10分)无锡市政府为了方便市民绿色出行,推出了共享单车服务.图①是某品牌共享单车放在水平地面上的实物图,图②是其示意图,其中AB、CD都与地面l平行,车轮半径为32cm,∠BCD=64°,BC=60cm,坐垫E与点B的距离BE为15cm.
(1)求坐垫E到地面的距离;
(2)根据经验,当坐垫E到CD的距离调整为人体腿长的0.8时,坐骑比较舒适.小明的腿长约为80cm,现将坐垫E调整至坐骑舒适高度位置E',求EE′的长.
(结果精确到0.1cm,参考数据:sin64°≈0.90,cos64°≈0.44,tan64°≈2.05)
25.(10分)某商店销售一种进价50元/件的商品,经市场调查发现:该商品的每天销售量y(件)是售价x(元/件)的一次函数,其售价、销售量的二组对应值如下表:
售价x(元/件) 55 65
销售量y(件/天) 90 70
(1)若某天销售利润为800元,求该天的售价为多少元/件?
(2)设该商店销售商品每天获得的利润为W(元),求W与x之间的函数关系式,并求出当销售单价定为多少时,该商店销售这种商品每天获得的利润最大?
26.(10分)【问题提出】如何用圆规和无刻度的直尺作一条直线或圆弧平分已知扇形的面积?
【初步尝试】如图1,已知扇形OAB,请你用圆规和无刻度的直尺过圆心O作一条直线,使扇形的面积被这条直线平分;
【问题联想】如图2,已知线段MN,请你用圆规和无刻度的直尺作一个以MN为斜边的等腰直角三角形MNP;
【问题再解】如图3,已知扇形OAB,请你用圆规和无刻度的直尺作一条以点O为圆心的圆弧,使扇形的面积被这条圆弧平分.
(友情提醒:以上作图均不写作法,但需保留作图痕迹)
27.(10分)如图,在Rt△ABC中,∠C=90°,AB=10cm,AC:BC=4:3,点P从点A出发沿AB方向向点B运动,速度为1cm/s,同时点Q从点B出发沿B→C→A方向向点A运动,速度为2cm/s,当一个运动点到达终点时,另一个运动点也随之停止运动.
(1)AC= cm;BC= cm;
(2)设点P的运动时间为x秒(x>0),△PBQ的面积为y cm2,当△PBQ存在时,求y与x的函数关系式,并写出自变量x的取值范围;
(3)当点Q在BC上运动时,多少秒时△PBQ的面积为15cm2?
28.(12分)如图a,抛物线y=ax2﹣2ax﹣b(a<0)与x轴的一个交点为B(﹣1,0),与y轴的正半轴交于点C,顶点为D.
(1)求顶点D的坐标(用含a的代数式表示);
(2)若以AD为直径的圆经过点C.
①求抛物线的解析式;
②如图b,点E是y轴负半轴上的一点,连接BE,将△OBE绕平面内某一点旋转180°,得到△PMN(点P、M、N分别和点O、B、E对应),并且点M、N都在抛物线上,作MF⊥x轴于点F,若线段MF:BF=1:2,求点M、N的坐标;
③如图c,点Q在抛物线的对称轴上,以Q为圆心的圆过A、B两点,并且和直线CD相切,求点Q的坐标.
2023-2024学年第一学期初三数学12月份作业检查试卷
参考答案
一、选择题(本大题共有10小题,每小题3分,共30分)
1 2 3 4 5 6 7 8 9 10
C D D D B B C A D A
二.填空题(本大题有8小题,每空3分,共24分)
11(2,1) 12. 3 13. 48π 14.
15. 7 16.﹣2<x<3 17.y=(x﹣2)2+4 18. 3
三、解答题(本大题共10小题,共96分,)
19.(8分)解方程:
解:(1)由原方程得:(x﹣1)2=25,
得x﹣1=±5, …………………………(2分)
解得x1=6,x2=﹣4, …………………………(4分)
(2)由原方程得:x2﹣4x=1,
得x2﹣4x+4=1+4,(x﹣2)2=5, …………………………(2分)
得,
解得,, …………………………(4分)
20.(8分)计算:
解:(1)原式= …………………………(2分)
=; …………………………(4分)
(2)原式= …………………………(2分)
=
=. …………………………(4分)
(10分)解:(1)如图1所示,△ADE即为所求;
…………………………(4分)
(2)如图2,
S△ADE=S△AME﹣S△AMD﹣S△EMD
=×10×10﹣×10×2﹣×10×4
=20,
故答案为:20; …………………………(7分)
(3)如图3,找到格点F,G,作BC,AC的垂直平分线DF,PG,交于点P,则点..即为所求,
∴P点的坐标为(1,5).
故答案为:(1,5). …………………………(10分)
22.(8分)(1)证明:∵四边形ABCD是矩形,
∴AD∥BC,∠B=90°,
∴∠DAF=∠AEB, …………………………(2分)
∵DF⊥AE,
∴∠AFD=90°=∠B,
∴△ADF∽△EAB; …………………………(4分)
(2)解:∵BC=AD=10,E是BC边的中点,
∴BE=5,
∴AE===13, …………………………(6分)
由(1)得:△ADF∽△EAB,
∴=,
即=,
解得:DF=. …………………………(4分)
23.(10分)解:(1)直线AD与圆O相切, …………………………(1分)
连接OA,
∵AD∥BC,
∴∠D=∠DBC,
∵AD=AB,
∴∠D=∠ABD,
∴∠DBC=∠ABD=30°, …………………………(3分)
∠BAD=120°,
∵OA=OB,
∴∠BAO=∠ABD=30°, …………………………(4分)
∴∠OAD=90°,
∴OA⊥AD,
∵OA是圆的半径,
∴直线AD与圆O相切, …………………………(5分)
(2)连接OC,作OH⊥BC于H,
∵OB=OC,
∴∠OCB=∠OBC=30°,
∴∠BOC=120°,
∴OH=OB=3,BH=OH=3,
∴BC=2BH=6,
∴扇形OBC的面积为:==12π, …………………………(7分)
∵S△OBC=BC OH=×6×3=9, …………………………(9分)
∴阴影部分的面积为:12π﹣9. …………………………(10分)
24.(10分)解:(1)如图1,过点E作EM⊥CD于点M,
由题意知∠BCM=64°、EC=BC+BE=60+15=75cm, …………………………(2分)
∴EM=ECsin∠BCM=75sin64°≈67.5(cm),
则单车车座E到地面的高度为67.5+32≈99.5(cm); …………………………(5分)
(2)如图2所示,过点E′作E′H⊥CD于点H,
由题意知E′H=80×0.8=64, …………………………(6分)
则E′C==≈71.1(cm), …………………………(8分)
∴EE′=CE﹣CE′=75﹣71.1=3.9(cm). …………………………(10分)
25.(10分)解:(1)依题意设y=kx+b,
则有,
解得:,
∴y=﹣2x+200,
若某天销售利润为800元, …………………………(2分)
则(x﹣50)(﹣2x+200)=800,
解得:x1=60,x2=90, …………………………(4分)
∴该天的售价为60元或者90元; …………………………(5分)
(2)根据题意得,
W=(x﹣50)(﹣2x+200)=﹣2x2+300x﹣10000=﹣2(x﹣75)2+1250,……(7分)
∵a=﹣2<0,
∴当x=75时,W有最大值1250, …………………………(9分)
答:当销售单价定为75元时利润最大 …………………………(10分)
26.(10分)解:【初步尝试】如图1,直线OP即为所求; ……………………(3分)
【问题联想】如图2,三角形MNP即为所求; …………………………(6分)
【问题再解】如图3中,即为所求. …………………………(10分)
27(10分).解:(1)设AC=4x cm,BC=3x cm,
在Rt△ABC中,AC2+BC2=AB2,
得(4x)2+(3x)2=102,
解得x=2(负值舍去),
∴AC=8cm,BC=6cm,
故答案为:8,6; …………………………(2分)
(2)解:如图2:当Q在BC上运动时,过Q作QH⊥AB于点H,
∵AP=x,BQ=2x,
∴PB=10﹣x,
∵∠BHQ=∠BCA=90°,∠QBH=∠ABC,
∴△BQH∽△BAC,
∴,
∴,
解得,
∴;………………(4分)
如图3:当Q在CA上运动时,过Q作QH′⊥AB于点H′,
∵AP=x,B→C→Q的路程为2x,
∴PB=10﹣x,AQ=14﹣2x,
∵∠AH′Q=∠ACB=90°,∠QAH′=∠BAC,
∴△AQH∽△ABC,
∴,
∴,
解得,
∴ …(6分)
综上,y=; …………………………(7分)
(3)解:当点Q在BC上运动时,,
当y=15时,,
解得,(舍去),
故当点Q在BC上运动时,秒时△PBQ的面积为15cm2. ……………………(10分)
28.(12分)解:(1)D(1,﹣4a). …………………………(2分)
(2)①有题设知∠ACD=90°;
a=﹣1,抛物线的解析式为y=﹣x2+2x+3. …………………………(5分)
②点M的坐标为(,);N(,). …………………………(8分)
③点Q(1,﹣4+2)或(1,﹣4﹣2).…………………………(12分)
同课章节目录
