30.4 二次函数的应用 第2课时 课件(共15张PPT) 冀教版九年级数学下册
文档属性
| 名称 | 30.4 二次函数的应用 第2课时 课件(共15张PPT) 冀教版九年级数学下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 369.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-27 10:00:05 | ||
图片预览





文档简介
(共15张PPT)
第三十章 二次函数
第2课时
30.4 二次函数的应用
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1. 能应用二次函数的性质解决图形中最大面积问题.
2.能应用二次函数的性质解决商品销售过程中的最大利润问题,能够弄清商品销售问题中的数量关系及确定自变量的取值范围.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
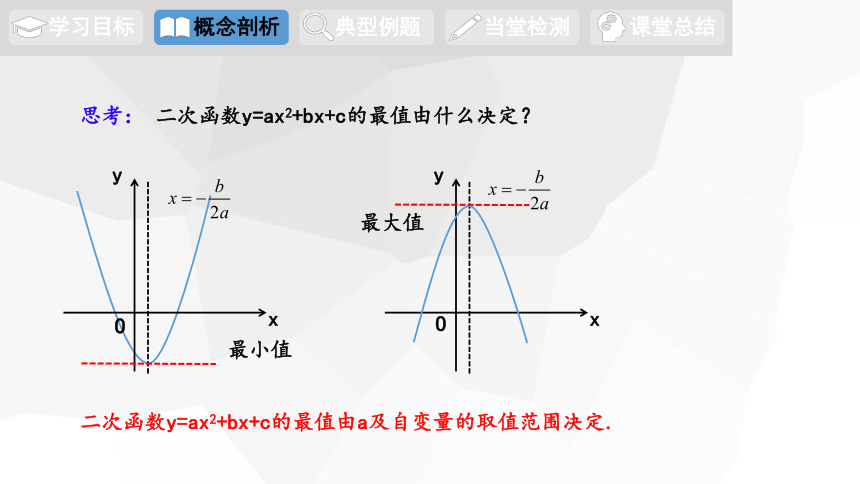
思考: 二次函数y=ax2+bx+c的最值由什么决定?
x
y
O
x
y
O
最小值
最大值
二次函数y=ax2+bx+c的最值由a及自变量的取值范围决定.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
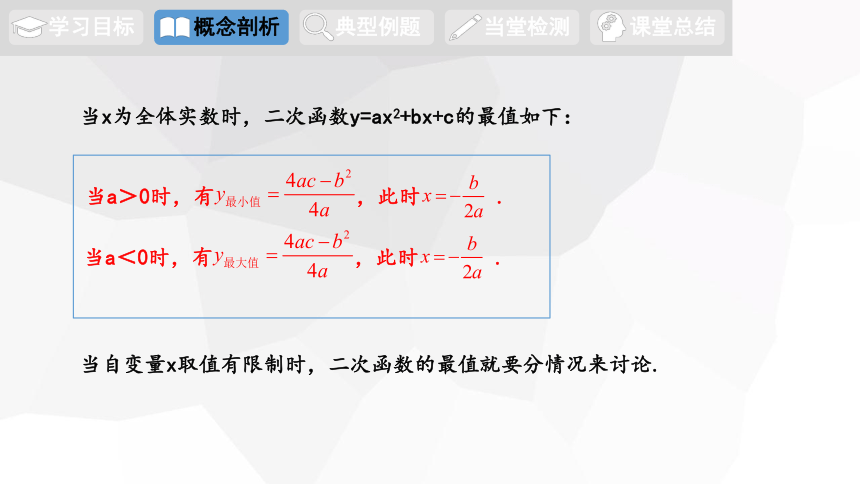
当x为全体实数时,二次函数y=ax2+bx+c的最值如下:
当a>0时,有 ,此时 .
当a<0时,有 ,此时 .
当自变量x取值有限制时,二次函数的最值就要分情况来讨论.
例1:如图,用一段长为60m的篱笆围成一个一边靠墙的矩形菜园,墙长18m,
这个矩形的长、宽各为多少时,菜园的面积最大,最大面积是多少?
解:设矩形面积为Sm2,与墙平行的一边为x米,则
(0<x≤18.)
当x=30,S取得最大值,但是由于x取值范围的限制,x取不到30.
因为二次项系数a<0,当x<30时,S随x的增大而增大.
故当x=18时,S有最大值是378.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
典型例题
当堂检测
学习目标
课堂总结
概念剖析
归纳总结
利用二次函数解决几何图形的最值问题:
1.求出函数解析式和自变量的取值范围;
2.配方变形,或利用公式求它的最大值或最小值,
3.检查求得的最大值或最小值对应的自变量的值必须在自变量的取值范围内.
1.小李想用篱笆围成一个周长为60米的矩形场地,矩形面积S(单位:
平方米)随矩形一边长x(单位:米)的变化而变化.
(1)求S与x之间的函数表达式,并写出自变量x的取值范围;
解:根据题意,得S=(60-2x)÷2·x=-x2+30x.
自变量x的取值范围是0<x<30.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1.小李想用篱笆围成一个周长为60米的矩形场地,矩形面积S(单位:
平方米)随矩形一边长x(单位:米)的变化而变化.
(2)当x是多少时,矩形场地面积S最大?最大面积是多少?
(2)S=-x2+30x=-(x-15)2+225.
所以S有最大值,即当x=15米时,S取得最大值,最大面积是225平方米.
因为a=-1<0,
典型例题
当堂检测
学习目标
课堂总结
概念剖析
例2:小明大学毕业回家乡创业,第一期培植盆景与花卉各50盆售后统计,
盆景的平均每盆利润是160元,花卉的平均每盆利润是19元,调研发现:
①盆景每增加1盆,盆景的平均每盆利润减少2元;每减少1盆,盆景的平均
每盆利润增加2元; ②花卉的平均每盆利润始终不变.
小明计划第二期培植盆景与花卉共100盆,设培植的盆景比第一期增加x盆,
第二期盆景与花卉售完后的利润分别为W1,W2(单位:元).
(1)用含x的代数式分别表示W1,W2;
(2)当x取何值时,第二期培植的盆景与花卉售完后获得的总利润W最大,
最大总利润是多少?
典型例题
当堂检测
学习目标
课堂总结
概念剖析
(1)用含x的代数式分别表示W1,W2;
解:第二期培植的盆景比第一期增加x盆,则第二期培植盆景(50+x)盆,
W2=19(50-x)=-19x+950.
W1=(50+x)(160-2x)=-2x2+60x+8000,
花卉[100-(50+x)]=(50-x)盆.由题意得
典型例题
当堂检测
学习目标
课堂总结
概念剖析
(2)当x取何值时,第二期培植的盆景与花卉售完后获得的总利润W最大,
最大总利润是多少?
解:(2)W总=W1+W2=-2x2+60x+8000+(-19x+950)=-2x2+41x+8950.
W总最大=-2×102+41×10+8950=9160(元).
故当x=10时,W总最大,
∵-2<0,-41÷[2×(-2)]=10.25,
典型例题
当堂检测
学习目标
课堂总结
概念剖析
典型例题
当堂检测
学习目标
课堂总结
概念剖析
归纳总结
利用二次函数求解商品利润问题的一般步骤:
(1)建立利润与价格之间的函数关系式:
运用“总利润=总售价-总成本”或“总利润=单件利润×销售量”
(2)结合实际意义,确定自变量的取值范围
(3)在自变量的取值范围内确定最大利润:可以利用配方法或公式求出最大利润;也可以画出函数的简图,利用简图和性质求出.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
2.某种商品每件的进价为20元,调查表明:在某段时间内若以每件x元(20 ≤x ≤30)出售,可卖出(30-x)件,使利润最大,则每件售价应定为 元.
25
3.进价为80元的某件定价100元时,每月可卖出2000件,价格每上涨1元,销售量便减少5件,那么每月售出衬衣的总件数y(件)与衬衣售价x(元)之间的函数关系式为 .每月利润w(元)与衬衣售价x(元)之间的函数关系式为 .(以上关系式只列式不化简).
y=2000-5(x-100)
w=[2000-5(x-100)](x-80)
典型例题
当堂检测
学习目标
课堂总结
概念剖析
w=[12+2(x-1)][80-4(x-1)]=(10+2x)(84-4x)
=-8x2+128x+840 =-8(x-8)2+1352.
4.一工艺师生产的某种产品按质量分为9个档次.第1档次(最低档次)的产品一天能生产80件,每件可获利润12元.产品每提高一个档次,每件产品的利润增加2元,但一天产量减少4件.如果只从生产利润这一角度考虑,他生产哪个档次的产品,可获得最大利润?
解:设生产x档次的产品时,每天所获得的利润为w元,则
当x=8时,w有最大值,且w最大=1352(元).
答:该工艺师生产第8档次产品,可使利润最大,最大利润为1352元.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
利用二次函数的最值解决问题
在实际问题中,利用二次函数的性质求最值,关键是由实际问题建立
二次函数模型,然后借助函数图象和实际问题中自变量的取值范围得出
函数的最值.
1.几何图形中的最值问题
注意:把函数问题转化为实际问题时,注意实际问题的取值范围.
2.商品利润的最值问题
第三十章 二次函数
第2课时
30.4 二次函数的应用
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1. 能应用二次函数的性质解决图形中最大面积问题.
2.能应用二次函数的性质解决商品销售过程中的最大利润问题,能够弄清商品销售问题中的数量关系及确定自变量的取值范围.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
思考: 二次函数y=ax2+bx+c的最值由什么决定?
x
y
O
x
y
O
最小值
最大值
二次函数y=ax2+bx+c的最值由a及自变量的取值范围决定.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
当x为全体实数时,二次函数y=ax2+bx+c的最值如下:
当a>0时,有 ,此时 .
当a<0时,有 ,此时 .
当自变量x取值有限制时,二次函数的最值就要分情况来讨论.
例1:如图,用一段长为60m的篱笆围成一个一边靠墙的矩形菜园,墙长18m,
这个矩形的长、宽各为多少时,菜园的面积最大,最大面积是多少?
解:设矩形面积为Sm2,与墙平行的一边为x米,则
(0<x≤18.)
当x=30,S取得最大值,但是由于x取值范围的限制,x取不到30.
因为二次项系数a<0,当x<30时,S随x的增大而增大.
故当x=18时,S有最大值是378.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
典型例题
当堂检测
学习目标
课堂总结
概念剖析
归纳总结
利用二次函数解决几何图形的最值问题:
1.求出函数解析式和自变量的取值范围;
2.配方变形,或利用公式求它的最大值或最小值,
3.检查求得的最大值或最小值对应的自变量的值必须在自变量的取值范围内.
1.小李想用篱笆围成一个周长为60米的矩形场地,矩形面积S(单位:
平方米)随矩形一边长x(单位:米)的变化而变化.
(1)求S与x之间的函数表达式,并写出自变量x的取值范围;
解:根据题意,得S=(60-2x)÷2·x=-x2+30x.
自变量x的取值范围是0<x<30.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1.小李想用篱笆围成一个周长为60米的矩形场地,矩形面积S(单位:
平方米)随矩形一边长x(单位:米)的变化而变化.
(2)当x是多少时,矩形场地面积S最大?最大面积是多少?
(2)S=-x2+30x=-(x-15)2+225.
所以S有最大值,即当x=15米时,S取得最大值,最大面积是225平方米.
因为a=-1<0,
典型例题
当堂检测
学习目标
课堂总结
概念剖析
例2:小明大学毕业回家乡创业,第一期培植盆景与花卉各50盆售后统计,
盆景的平均每盆利润是160元,花卉的平均每盆利润是19元,调研发现:
①盆景每增加1盆,盆景的平均每盆利润减少2元;每减少1盆,盆景的平均
每盆利润增加2元; ②花卉的平均每盆利润始终不变.
小明计划第二期培植盆景与花卉共100盆,设培植的盆景比第一期增加x盆,
第二期盆景与花卉售完后的利润分别为W1,W2(单位:元).
(1)用含x的代数式分别表示W1,W2;
(2)当x取何值时,第二期培植的盆景与花卉售完后获得的总利润W最大,
最大总利润是多少?
典型例题
当堂检测
学习目标
课堂总结
概念剖析
(1)用含x的代数式分别表示W1,W2;
解:第二期培植的盆景比第一期增加x盆,则第二期培植盆景(50+x)盆,
W2=19(50-x)=-19x+950.
W1=(50+x)(160-2x)=-2x2+60x+8000,
花卉[100-(50+x)]=(50-x)盆.由题意得
典型例题
当堂检测
学习目标
课堂总结
概念剖析
(2)当x取何值时,第二期培植的盆景与花卉售完后获得的总利润W最大,
最大总利润是多少?
解:(2)W总=W1+W2=-2x2+60x+8000+(-19x+950)=-2x2+41x+8950.
W总最大=-2×102+41×10+8950=9160(元).
故当x=10时,W总最大,
∵-2<0,-41÷[2×(-2)]=10.25,
典型例题
当堂检测
学习目标
课堂总结
概念剖析
典型例题
当堂检测
学习目标
课堂总结
概念剖析
归纳总结
利用二次函数求解商品利润问题的一般步骤:
(1)建立利润与价格之间的函数关系式:
运用“总利润=总售价-总成本”或“总利润=单件利润×销售量”
(2)结合实际意义,确定自变量的取值范围
(3)在自变量的取值范围内确定最大利润:可以利用配方法或公式求出最大利润;也可以画出函数的简图,利用简图和性质求出.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
2.某种商品每件的进价为20元,调查表明:在某段时间内若以每件x元(20 ≤x ≤30)出售,可卖出(30-x)件,使利润最大,则每件售价应定为 元.
25
3.进价为80元的某件定价100元时,每月可卖出2000件,价格每上涨1元,销售量便减少5件,那么每月售出衬衣的总件数y(件)与衬衣售价x(元)之间的函数关系式为 .每月利润w(元)与衬衣售价x(元)之间的函数关系式为 .(以上关系式只列式不化简).
y=2000-5(x-100)
w=[2000-5(x-100)](x-80)
典型例题
当堂检测
学习目标
课堂总结
概念剖析
w=[12+2(x-1)][80-4(x-1)]=(10+2x)(84-4x)
=-8x2+128x+840 =-8(x-8)2+1352.
4.一工艺师生产的某种产品按质量分为9个档次.第1档次(最低档次)的产品一天能生产80件,每件可获利润12元.产品每提高一个档次,每件产品的利润增加2元,但一天产量减少4件.如果只从生产利润这一角度考虑,他生产哪个档次的产品,可获得最大利润?
解:设生产x档次的产品时,每天所获得的利润为w元,则
当x=8时,w有最大值,且w最大=1352(元).
答:该工艺师生产第8档次产品,可使利润最大,最大利润为1352元.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
利用二次函数的最值解决问题
在实际问题中,利用二次函数的性质求最值,关键是由实际问题建立
二次函数模型,然后借助函数图象和实际问题中自变量的取值范围得出
函数的最值.
1.几何图形中的最值问题
注意:把函数问题转化为实际问题时,注意实际问题的取值范围.
2.商品利润的最值问题
