31.3 用频率估计概率 课件(共16张PPT) 冀教版数学九年级下册
文档属性
| 名称 | 31.3 用频率估计概率 课件(共16张PPT) 冀教版数学九年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 388.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-27 00:00:00 | ||
图片预览





文档简介
(共16张PPT)
第三十一章 随机事件的概率
31.3 用频率估计概率
合作探究
当堂检测
学习目标
课堂总结
自主学习
1.理解试验次数较大时试验频率趋于稳定这一规律
2.结合具体情境掌握如何用频率估计概率(重点)
合作探究
当堂检测
学习目标
课堂总结
自主学习
抛掷一枚均匀的硬币,硬币落下后,会出现两种情况:
正面朝上
正面朝下
你认为正面朝上和正面朝下的可能性相同吗
问题引入
合作探究
当堂检测
学习目标
课堂总结
自主学习
探究:用频率估计概率
(1) 同桌两人做20次掷硬币的游戏,并记录在下表中:
试验总次数
正面朝上的次数
正面朝下的次数
正面朝上的频率
正面朝下的频率
实验探究:
合作探究
当堂检测
学习目标
课堂总结
自主学习
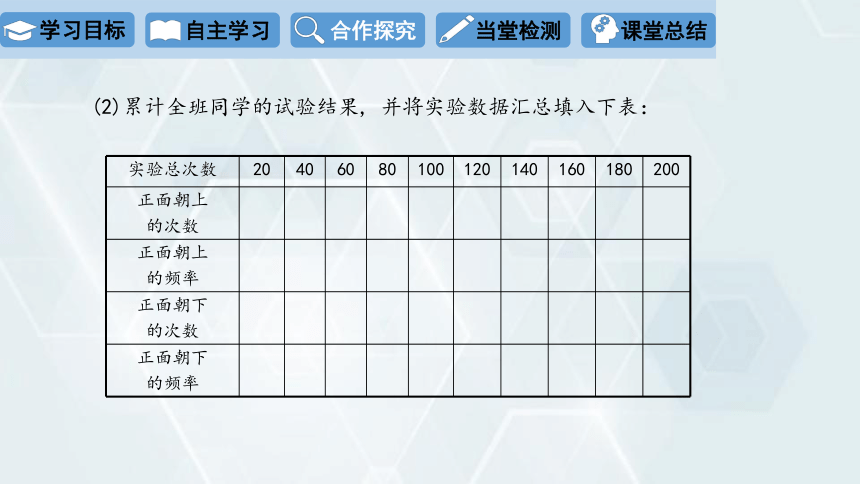
(2)累计全班同学的试验结果, 并将实验数据汇总填入下表:
实验总次数 20 40 60 80 100 120 140 160 180 200
正面朝上 的次数
正面朝上 的频率
正面朝下 的次数
正面朝下 的频率
合作探究
当堂检测
学习目标
课堂总结
自主学习
20
40
60
80
100
120
140
160
180
200
0.5
0
1.0
0.2
0.7
频率
实验总次数
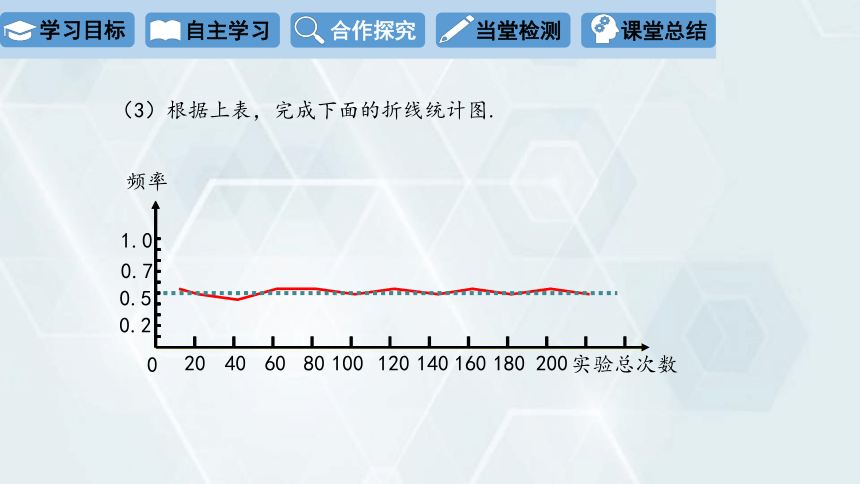
(3)根据上表,完成下面的折线统计图.
合作探究
当堂检测
学习目标
课堂总结
自主学习
当试验次数很多时, 正面朝上的频率折线差不多稳定在“ 0.5 水平直线” 上.
(4)观察上面的折线统计图,你发现了什么规律?
当实验的次数较少时,折线在“0.5水平直线”的上下摆动的幅度较大,随着实验的次数的增加,折线在“0.5水平直线”的上下摆动的幅度会逐渐变小.
合作探究
当堂检测
学习目标
课堂总结
自主学习
大量实验表明,随着试验次数的增大,事件发生的频率逐渐稳定到它的概率,或者说概率是频率的稳定值,这就是频率的稳定性.
一般地,大量重复的试验中,我们常用随机事件A发生的频率来估计事件A发生的概率.
归纳总结
合作探究
当堂检测
学习目标
课堂总结
自主学习
某瓷砖厂对最近出炉的一大批某型号瓷砖进行质量抽检,结果如下:
(1)估计这种瓷砖的合格品率(精确到0.01);
(2)若该厂本月生产该型号瓷砖500000块,试估计合格品数.
抽取瓷砖数n 100 200 300 400 500 600 800 1000 2000
合格品数m 95 192 287 385 481 577 770 961 1924
合格品率 0.950 0.960 0.957 0.963 0.962 0.962 0.963 0.961 0.962
试一试:
解:(1)观察上表,可以发现,当抽取的瓷砖数n≥400时,合格品率稳定在0.962的附近,所以我们可取P=0.96作为该型号瓷砖的合格品率的估计.
(2)500000×96%=480000(块),可以估计该型号合格品数为480000块.
合作探究
当堂检测
学习目标
课堂总结
自主学习
频率与概率的关系
联系: 频率 概率
事件发生的频繁程度
事件发生的
可能性大小
在实际中,我们常用比较稳定的频率估计事件的概率,而试验次数越大,得到概率的精确估计值的可能性就越大.
区别:频率本身是随机的,在试验前不能确定,做同样次数或不同次数的重复试验得到的事件的频率都可能不同,而概率是一个确定数,是客观存在的,与每次试验无关.
稳定性
大量重复试验
归纳总结
合作探究
当堂检测
学习目标
课堂总结
自主学习
练一练:
1.某厂打算生产一种中学生使用的笔袋,但无法确定各种颜色的产量,于是该文具厂就笔袋的颜色随机调查了5000名中学生,并在调查到1000名、2000名、3000名、4000名、5000名时分别计算了各种颜色的频率,绘制折线图如下:
(1)随着调查次数的增加,红色的频率如何变化?
随着调查次数的增加,红色的频率基本稳定在40%左右.
合作探究
当堂检测
学习目标
课堂总结
自主学习
(3)若你是该厂的负责人,你将如何安排生产各种颜色的产量?
红、黄、蓝、绿及其它颜色的生产比例大约为4:2:1:2:1 .
(2)你能估计调查到10000名同学时,红色的频率是多少吗?
估计调查到10000名同学时,红色的频率大约仍是40%左右.
合作探究
当堂检测
学习目标
课堂总结
自主学习
1.在一个不透明的布袋中装有红色、白色玻璃球共60个,除颜色外其他完全相同.小明通过多次摸球试验后发现,其中摸到红色球的频率稳定在25%左右,则口袋中红色球可能有( )
A.5个 B.10个 C.15个 D.45个
C
合作探究
当堂检测
学习目标
课堂总结
自主学习
2.对某批乒乓球的质量进行随机抽查,如下表所示:
随机抽取的乒乓球数 n 10 20 50 100 200 500 1000
优等品数 m 7 16 43 81 164 414 825
优等品率m/n
(1)完成上表;
0.7
0.8
0.86
0.81
0.82
0.828
0.825
合作探究
当堂检测
学习目标
课堂总结
自主学习
(3)如果重新再抽取1000个乒乓球进行质量检查,对比上表记录下数据,两表的结果会一样吗?为什么?
(2)根据上表,在这批乒乓球中任取一个,它为优等品的概率是多少?
0.8
答:不一定,这是因为频数和频率的随机性.
合作探究
当堂检测
学习目标
课堂总结
自主学习
用频率估计概率
1.频率的稳定性:大量实验表明,随着试验次数的增大,事件发生的频率逐渐稳定到它的概率,或者说概率是频率的稳定值.
2.用频率估计概率:在实际中,我们常用比较稳定的频率估计事件的概率,而试验次数越大,得到概率的精确估计值的可能性就越大.
第三十一章 随机事件的概率
31.3 用频率估计概率
合作探究
当堂检测
学习目标
课堂总结
自主学习
1.理解试验次数较大时试验频率趋于稳定这一规律
2.结合具体情境掌握如何用频率估计概率(重点)
合作探究
当堂检测
学习目标
课堂总结
自主学习
抛掷一枚均匀的硬币,硬币落下后,会出现两种情况:
正面朝上
正面朝下
你认为正面朝上和正面朝下的可能性相同吗
问题引入
合作探究
当堂检测
学习目标
课堂总结
自主学习
探究:用频率估计概率
(1) 同桌两人做20次掷硬币的游戏,并记录在下表中:
试验总次数
正面朝上的次数
正面朝下的次数
正面朝上的频率
正面朝下的频率
实验探究:
合作探究
当堂检测
学习目标
课堂总结
自主学习
(2)累计全班同学的试验结果, 并将实验数据汇总填入下表:
实验总次数 20 40 60 80 100 120 140 160 180 200
正面朝上 的次数
正面朝上 的频率
正面朝下 的次数
正面朝下 的频率
合作探究
当堂检测
学习目标
课堂总结
自主学习
20
40
60
80
100
120
140
160
180
200
0.5
0
1.0
0.2
0.7
频率
实验总次数
(3)根据上表,完成下面的折线统计图.
合作探究
当堂检测
学习目标
课堂总结
自主学习
当试验次数很多时, 正面朝上的频率折线差不多稳定在“ 0.5 水平直线” 上.
(4)观察上面的折线统计图,你发现了什么规律?
当实验的次数较少时,折线在“0.5水平直线”的上下摆动的幅度较大,随着实验的次数的增加,折线在“0.5水平直线”的上下摆动的幅度会逐渐变小.
合作探究
当堂检测
学习目标
课堂总结
自主学习
大量实验表明,随着试验次数的增大,事件发生的频率逐渐稳定到它的概率,或者说概率是频率的稳定值,这就是频率的稳定性.
一般地,大量重复的试验中,我们常用随机事件A发生的频率来估计事件A发生的概率.
归纳总结
合作探究
当堂检测
学习目标
课堂总结
自主学习
某瓷砖厂对最近出炉的一大批某型号瓷砖进行质量抽检,结果如下:
(1)估计这种瓷砖的合格品率(精确到0.01);
(2)若该厂本月生产该型号瓷砖500000块,试估计合格品数.
抽取瓷砖数n 100 200 300 400 500 600 800 1000 2000
合格品数m 95 192 287 385 481 577 770 961 1924
合格品率 0.950 0.960 0.957 0.963 0.962 0.962 0.963 0.961 0.962
试一试:
解:(1)观察上表,可以发现,当抽取的瓷砖数n≥400时,合格品率稳定在0.962的附近,所以我们可取P=0.96作为该型号瓷砖的合格品率的估计.
(2)500000×96%=480000(块),可以估计该型号合格品数为480000块.
合作探究
当堂检测
学习目标
课堂总结
自主学习
频率与概率的关系
联系: 频率 概率
事件发生的频繁程度
事件发生的
可能性大小
在实际中,我们常用比较稳定的频率估计事件的概率,而试验次数越大,得到概率的精确估计值的可能性就越大.
区别:频率本身是随机的,在试验前不能确定,做同样次数或不同次数的重复试验得到的事件的频率都可能不同,而概率是一个确定数,是客观存在的,与每次试验无关.
稳定性
大量重复试验
归纳总结
合作探究
当堂检测
学习目标
课堂总结
自主学习
练一练:
1.某厂打算生产一种中学生使用的笔袋,但无法确定各种颜色的产量,于是该文具厂就笔袋的颜色随机调查了5000名中学生,并在调查到1000名、2000名、3000名、4000名、5000名时分别计算了各种颜色的频率,绘制折线图如下:
(1)随着调查次数的增加,红色的频率如何变化?
随着调查次数的增加,红色的频率基本稳定在40%左右.
合作探究
当堂检测
学习目标
课堂总结
自主学习
(3)若你是该厂的负责人,你将如何安排生产各种颜色的产量?
红、黄、蓝、绿及其它颜色的生产比例大约为4:2:1:2:1 .
(2)你能估计调查到10000名同学时,红色的频率是多少吗?
估计调查到10000名同学时,红色的频率大约仍是40%左右.
合作探究
当堂检测
学习目标
课堂总结
自主学习
1.在一个不透明的布袋中装有红色、白色玻璃球共60个,除颜色外其他完全相同.小明通过多次摸球试验后发现,其中摸到红色球的频率稳定在25%左右,则口袋中红色球可能有( )
A.5个 B.10个 C.15个 D.45个
C
合作探究
当堂检测
学习目标
课堂总结
自主学习
2.对某批乒乓球的质量进行随机抽查,如下表所示:
随机抽取的乒乓球数 n 10 20 50 100 200 500 1000
优等品数 m 7 16 43 81 164 414 825
优等品率m/n
(1)完成上表;
0.7
0.8
0.86
0.81
0.82
0.828
0.825
合作探究
当堂检测
学习目标
课堂总结
自主学习
(3)如果重新再抽取1000个乒乓球进行质量检查,对比上表记录下数据,两表的结果会一样吗?为什么?
(2)根据上表,在这批乒乓球中任取一个,它为优等品的概率是多少?
0.8
答:不一定,这是因为频数和频率的随机性.
合作探究
当堂检测
学习目标
课堂总结
自主学习
用频率估计概率
1.频率的稳定性:大量实验表明,随着试验次数的增大,事件发生的频率逐渐稳定到它的概率,或者说概率是频率的稳定值.
2.用频率估计概率:在实际中,我们常用比较稳定的频率估计事件的概率,而试验次数越大,得到概率的精确估计值的可能性就越大.
