31.4 用列举法求简单事件的概率 第2课时 课件(共17张PPT) 冀教版九年级数学下册
文档属性
| 名称 | 31.4 用列举法求简单事件的概率 第2课时 课件(共17张PPT) 冀教版九年级数学下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-27 00:00:00 | ||
图片预览






文档简介
(共17张PPT)
第三十一章 随机事件的概率
31.4 用列举法求简单事件的概率
第2课时
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1.进一步理解等可能事件概率的意义.
2.学习运用树形图计算事件的概率.(重点)
典型例题
当堂检测
学习目标
课堂总结
概念剖析
试一试:根据所学的知识,试着完成下面的内容。
抛掷一枚硬币,连续抛掷三次,会有哪些可能的情况?
抛掷1次
抛掷2次
抛掷3次
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1
画树状图法求概率
树状图法
按事件发生的次序,列出事件可能出现的结果,其树形图如图.
树状图法的一般步骤:
(1)弄清楚每一步有几种结果;
(2)根据树状图对应写出所有可能的结果;
(3)利用概率公式进行计算.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
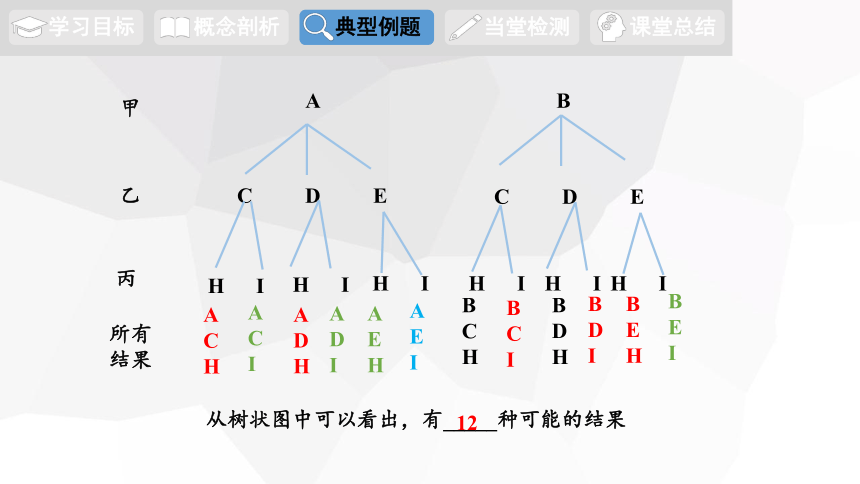
例1:甲口袋中装有2个小球,它们分别写有字母A和B,乙口袋中装3个小球,它们分别写有字母C、D和E;丙口袋中装有2个小球,它们分别写有字母H和I,从三个口袋中各随机取出1个小球.
(1)取出的3个小球上恰好有1个、2个、3个元音字母的概率分别是多少?
(2)取出的3个小球上全部是辅音字母的概率是多少?
提示:采用树状图法可以无遗漏、清晰地列举出所有可能的情况.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
丙
甲
乙
B
A
E
C
D
E
C
D
I
H
I
H
I
H
I
H
I
H
I
H
ACH
ACI
ADH
ADI
AEH
AEI
BCH
BCI
BDH
BDI
BEH
BEI
从树状图中可以看出,有_____种可能的结果
12
所有结果
典型例题
当堂检测
学习目标
课堂总结
概念剖析
解:(1)取出的3个小球上恰好有1个元音字母的结果有5种,即ACH、ADH、BCI、BDI、BEH,所以
恰好有2个元音字母的结果有4种,即ACI、ADI、AEH、BEI,所以
全部为元音字母的结果有1种,即AEI,所以
(2)取出的3个小球上全部是辅音字母的结果有2种,即BCH、BDH,所以
P(1个元音)=
P(2个元音)=
P(3个元音)=
P(3个辅音)=
典型例题
当堂检测
学习目标
课堂总结
概念剖析
树状图用于分析具有两个或两个以上因素的试验.在画树状图时,每一行都表示一个因素.为分析方便,一般把因素中分支多的安排在上面.
归纳总结:
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1.如图,一只蚂蚁从点A出发到点D,E,F处寻觅食物.假定蚂蚁在每个岔路口都等可能地随机选择一条向左下或右下的路径(比如A岔口可以向左下到达B处,也可以向右下到达C处,其中A,B,C都是岔路口),那么,蚂蚁从A出发到达E处的概率是________.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
2.现在学校决定由甲同学代表学校参加全县的诗歌朗诵比赛,甲同学有3件上衣,分别为红色(R)、黄色(Y)、蓝色(B),有2条裤子,分别为蓝色(B)和棕色(b)。甲同学想要穿蓝色上衣和蓝色裤子参加比赛,你知道甲同学任意拿出1件上衣和1条裤子,恰好是蓝色上衣和蓝色裤子的概率是多少吗?
上衣:
裤子:
典型例题
当堂检测
学习目标
课堂总结
概念剖析
解:用“树状图”列出所有可能出现的结果:
每种结果的出现是等可能的.“取出1件蓝色上衣和1条蓝色裤子”记为事件A,那么事件A发生的概率是P(A)=
开始
上衣
裤子
所有可能出现的结果
所以,甲同学恰好穿上蓝色上衣和蓝色裤子的概率是
典型例题
当堂检测
学习目标
课堂总结
概念剖析
2
列表法和树状图法的区别
想一想:什么时候用“列表法”方便什么时候用“树形图”方便?
当一次试验涉及3个因素或3个以上的因素时,列表法就不方便了,为了不重复不遗漏地列出所有可能的结果,通常用树形图。
当一次试验涉及两个因素时,且可能出现的结果较多时,为了不重复不遗漏地列出所有可能的结果,通常用列表法。
例2:甲、乙、丙三人做传球的游戏,开始时,球在甲手中,每次传球,持球的人将球任意传给其余两人中的一人,如此传球三次.
(1)写出三次传球的所有可能结果(即传球的方式);
(2)指定事件A:“传球三次后,球又回到甲的手中”,写出A发生的所有可能结果;
(3)求P(A).
典型例题
当堂检测
学习目标
课堂总结
概念剖析
解:(1)
第二次
第三次
结果
开始:甲
共有八种可能的结果,每种结果出现的可能性相同;
(2)传球三次后,球又回到甲手中,事件A发生有两种可能出现结果(乙,丙,甲)(丙,乙,甲)
(3)P(A)=
乙
丙
第一次
甲
甲
丙
乙
甲
甲
丙
丙
乙
乙
乙
丙
(丙,乙,丙)
(乙,甲,丙)
(乙,丙,甲)
(乙,丙,乙)
(丙,甲,乙)
(丙,甲,丙)
(丙,乙,甲)
(乙,甲,乙)
典型例题
当堂检测
学习目标
课堂总结
概念剖析
方法归纳
当试验包含两步时,列表法比较方便;当然,此时也可以用树形图法;
当事件要经过多个(三个或三个以上)步骤完成时,应选用树状图法求事件的概率.
思考:你能够用列表法写出3次传球的所有可能结果吗?
若再用列表法表示所有结果已经不方便!
典型例题
当堂检测
学习目标
课堂总结
概念剖析
典型例题
当堂检测
学习目标
课堂总结
概念剖析
3.一天晚上,小伟帮助妈妈清洗两个只有颜色不同的有盖茶杯,突然停电了,小伟只好把杯盖和茶杯随机地搭配在一起,则颜色搭配正确的概率是________.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
用树状图法求概率
步骤
注意
①关键要弄清楚每一步有几种结果;
②在树状图下面对应写出所有可能的结果;
③利用概率公式进行计算.
试验涉及试验因素个数或试验步骤分几步
第三十一章 随机事件的概率
31.4 用列举法求简单事件的概率
第2课时
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1.进一步理解等可能事件概率的意义.
2.学习运用树形图计算事件的概率.(重点)
典型例题
当堂检测
学习目标
课堂总结
概念剖析
试一试:根据所学的知识,试着完成下面的内容。
抛掷一枚硬币,连续抛掷三次,会有哪些可能的情况?
抛掷1次
抛掷2次
抛掷3次
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1
画树状图法求概率
树状图法
按事件发生的次序,列出事件可能出现的结果,其树形图如图.
树状图法的一般步骤:
(1)弄清楚每一步有几种结果;
(2)根据树状图对应写出所有可能的结果;
(3)利用概率公式进行计算.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
例1:甲口袋中装有2个小球,它们分别写有字母A和B,乙口袋中装3个小球,它们分别写有字母C、D和E;丙口袋中装有2个小球,它们分别写有字母H和I,从三个口袋中各随机取出1个小球.
(1)取出的3个小球上恰好有1个、2个、3个元音字母的概率分别是多少?
(2)取出的3个小球上全部是辅音字母的概率是多少?
提示:采用树状图法可以无遗漏、清晰地列举出所有可能的情况.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
丙
甲
乙
B
A
E
C
D
E
C
D
I
H
I
H
I
H
I
H
I
H
I
H
ACH
ACI
ADH
ADI
AEH
AEI
BCH
BCI
BDH
BDI
BEH
BEI
从树状图中可以看出,有_____种可能的结果
12
所有结果
典型例题
当堂检测
学习目标
课堂总结
概念剖析
解:(1)取出的3个小球上恰好有1个元音字母的结果有5种,即ACH、ADH、BCI、BDI、BEH,所以
恰好有2个元音字母的结果有4种,即ACI、ADI、AEH、BEI,所以
全部为元音字母的结果有1种,即AEI,所以
(2)取出的3个小球上全部是辅音字母的结果有2种,即BCH、BDH,所以
P(1个元音)=
P(2个元音)=
P(3个元音)=
P(3个辅音)=
典型例题
当堂检测
学习目标
课堂总结
概念剖析
树状图用于分析具有两个或两个以上因素的试验.在画树状图时,每一行都表示一个因素.为分析方便,一般把因素中分支多的安排在上面.
归纳总结:
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1.如图,一只蚂蚁从点A出发到点D,E,F处寻觅食物.假定蚂蚁在每个岔路口都等可能地随机选择一条向左下或右下的路径(比如A岔口可以向左下到达B处,也可以向右下到达C处,其中A,B,C都是岔路口),那么,蚂蚁从A出发到达E处的概率是________.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
2.现在学校决定由甲同学代表学校参加全县的诗歌朗诵比赛,甲同学有3件上衣,分别为红色(R)、黄色(Y)、蓝色(B),有2条裤子,分别为蓝色(B)和棕色(b)。甲同学想要穿蓝色上衣和蓝色裤子参加比赛,你知道甲同学任意拿出1件上衣和1条裤子,恰好是蓝色上衣和蓝色裤子的概率是多少吗?
上衣:
裤子:
典型例题
当堂检测
学习目标
课堂总结
概念剖析
解:用“树状图”列出所有可能出现的结果:
每种结果的出现是等可能的.“取出1件蓝色上衣和1条蓝色裤子”记为事件A,那么事件A发生的概率是P(A)=
开始
上衣
裤子
所有可能出现的结果
所以,甲同学恰好穿上蓝色上衣和蓝色裤子的概率是
典型例题
当堂检测
学习目标
课堂总结
概念剖析
2
列表法和树状图法的区别
想一想:什么时候用“列表法”方便什么时候用“树形图”方便?
当一次试验涉及3个因素或3个以上的因素时,列表法就不方便了,为了不重复不遗漏地列出所有可能的结果,通常用树形图。
当一次试验涉及两个因素时,且可能出现的结果较多时,为了不重复不遗漏地列出所有可能的结果,通常用列表法。
例2:甲、乙、丙三人做传球的游戏,开始时,球在甲手中,每次传球,持球的人将球任意传给其余两人中的一人,如此传球三次.
(1)写出三次传球的所有可能结果(即传球的方式);
(2)指定事件A:“传球三次后,球又回到甲的手中”,写出A发生的所有可能结果;
(3)求P(A).
典型例题
当堂检测
学习目标
课堂总结
概念剖析
解:(1)
第二次
第三次
结果
开始:甲
共有八种可能的结果,每种结果出现的可能性相同;
(2)传球三次后,球又回到甲手中,事件A发生有两种可能出现结果(乙,丙,甲)(丙,乙,甲)
(3)P(A)=
乙
丙
第一次
甲
甲
丙
乙
甲
甲
丙
丙
乙
乙
乙
丙
(丙,乙,丙)
(乙,甲,丙)
(乙,丙,甲)
(乙,丙,乙)
(丙,甲,乙)
(丙,甲,丙)
(丙,乙,甲)
(乙,甲,乙)
典型例题
当堂检测
学习目标
课堂总结
概念剖析
方法归纳
当试验包含两步时,列表法比较方便;当然,此时也可以用树形图法;
当事件要经过多个(三个或三个以上)步骤完成时,应选用树状图法求事件的概率.
思考:你能够用列表法写出3次传球的所有可能结果吗?
若再用列表法表示所有结果已经不方便!
典型例题
当堂检测
学习目标
课堂总结
概念剖析
典型例题
当堂检测
学习目标
课堂总结
概念剖析
3.一天晚上,小伟帮助妈妈清洗两个只有颜色不同的有盖茶杯,突然停电了,小伟只好把杯盖和茶杯随机地搭配在一起,则颜色搭配正确的概率是________.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
用树状图法求概率
步骤
注意
①关键要弄清楚每一步有几种结果;
②在树状图下面对应写出所有可能的结果;
③利用概率公式进行计算.
试验涉及试验因素个数或试验步骤分几步
