1.3 补集与集合的综合运算 课件(共24张PPT)——高中数学人教A版(2019)必修第一册
文档属性
| 名称 | 1.3 补集与集合的综合运算 课件(共24张PPT)——高中数学人教A版(2019)必修第一册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 549.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-27 00:00:00 | ||
图片预览








文档简介
(共24张PPT)
人教高中A版必修一数学课件
补集与集合的综合运算
集合与常用逻辑用语
一
二
知识点一、全集
1.思考
全集一定包含任何元素吗
提示:不一定.只要含有所有所要研究的对象即可做全集.换一句话说,所研究对象对应的集合一定为该全集的子集.
2.填空.
在研究集合与集合之间的关系时,如果所要研究的集合都是 某一给定集合的子集,那么称这个给定的集合为全集,通常用U表示.
一
二
知识点二、补集
1.思考
(1)已知U={a,b,c,d,e,f},A={b,f},如果从全集U中去掉集合A中的元素,剩下的元素构成的集合是什么
提示:剩余元素构成的集合为{a,c,d,e}.
(2)上述问题中所求得的集合应该怎样命名
提示:集合{a,c,d,e}可称为子集A在全集U中的补集.符号表示为: UA={a,c,d,e}.
一
二
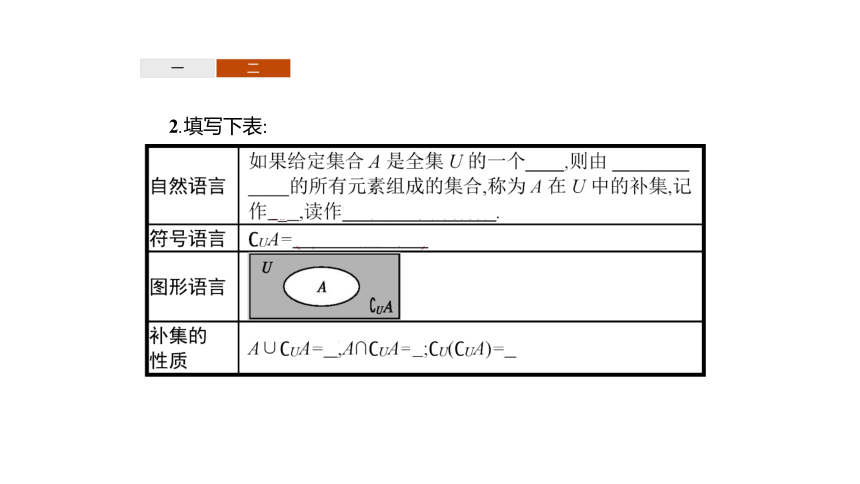
2.填写下表:
一
二
3.做一做
(1)若U={x|x>0},A={x|x>3},则 UA= .
答案:{x|0(2)如图所示的阴影部分表示的集合是( )
A.A∩( UB) B.B∩( UA)
C. U(A∩B) D. U(A∪B)
答案:B
(3)判断下列说法是否正确,正确的在后面的括号里打“√”,错误的打“×”.
①对任意集合A,B,U为全集,均有 U(A∩B)=( UA)∪( UB).( )
②对任意集合A,B,U为全集,均有 U(A∪B)=( UA)∩( UB).( )
③A∩( RA)=R.( )
④若A= ,则 R = .( )
答案:①√ ②√ ③× ④×
探究一
探究二
探究三
思想方法
集合的补集运算
例1 已知全集U=R,集合A={x|-3求:(1) UA, UB;
(2) U(A∩B).
分析:(1)根据补集的定义,借助于数轴写出;(2)先求A∩B,再根据补集的定义写出.
解:(1)∵A={x|-3在数轴上分别表示出集合A,B,如图所示.
∴ UA={x|x≤-3或x≥3}, UB={x|x≥1}.
(2)∵A∩B={x|-3
∴ U(A∩B)={x|x≥1或x≤-3}.
当堂检测
探究一
探究二
探究三
思想方法
反思感悟求集合补集的解题策略
1.如果所给集合是有限集,则先把集合中的元素一一列举出来,再结合补集的定义来求解.另外针对此类问题,在解答过程中也常常借助于维恩图来求解.这样处理起来,相对来说比较直观、形象且解答时不易出错.
2.如果所给集合是无限集,则常借助于数轴,先把已知集合及全集分别表示在数轴上,再根据补集的定义求解,这样处理比较形象直观,解答过程中注意端点值能否取得.
当堂检测
探究一
探究二
探究三
思想方法
变式训练1求解下列各题:
(1)设全集U=R,集合A={x|0≤x<3},则 UA= ;
(2)设全集U={三角形},集合A={直角三角形},则 UA= .
解析:(1)
由于全集U=R,画出数轴(如图所示),由补集的定义可得 UA={x|x<0,或x≥3}.
(2)∵U={三角形},A={直角三角形},
∴ UA={锐角三角形,或钝角三角形}.
答案:(1){x|x<0,或x≥3}
(2){锐角三角形,或钝角三角形}
当堂检测
探究一
探究二
探究三
思想方法
交集、并集、补集的综合运算
例2 已知全集U={x|x≤4},集合A={x|-2分析:可借助数轴分析求解.
解:把全集U和集合A,B在数轴上表示(如图所示),
由图可知 UA={x|x≤-2,或3≤x≤4},
A∩B={x|-2 U(A∩B)={x|x≤-2,或3≤x≤4},
( UA)∩B={x|-3当堂检测
探究一
探究二
探究三
思想方法
反思感悟集合运算的解题技巧
1.对于无限集,常借助于数轴,先把已知集合及全集分别表示在数轴上,再根据交、并、补的定义求解,这样处理比较形象直观,解答过程中注意端点的“取”与“舍”.
2.对于有限集,应先把集合中的元素一一列举出来,再结合交、并、补集的定义来求解,另外针对此类问题,在解答过程中也常常借助于维恩图来求解,这样处理起来,相对来说比较直观、形象,且解答时不易出错.
当堂检测
探究一
探究二
探究三
思想方法
变式训练2集合A={x|-1≤x≤2},B={x|x<1},则A∩( RB)=( )
A.{x|x>1} B.{x|x≥1}
C.{x|1答案:D
当堂检测
探究一
探究二
探究三
思想方法
补集运算中的含参数问题
例3 (1)设全集U={2,3,a2+2a-3},A={|a+1|,2}, UA={5},则a等于 ;
(2)已知集合A={x|x解析:(1)由 UA={5},知a2+2a-3=5,解得a=-4或a=2.
当a=-4时,U={2,3,5},A={3,2},满足 UA={5};
当a=2时,U={2,3,5},A={3,2},满足 UA={5}.所以a的值为-4或2.
(2) RB={x|x≤1,或x≥2},由于A∪ RB=R,如图所示,所以a≥2.
答案:(1)-4或2 (2)a≥2
当堂检测
探究一
探究二
探究三
思想方法
反思感悟1.由集合补集求有关参数问题的思路流程:
2.含参数问题一般要用到分类讨论思想、等价转化思想及数形结合思想来解决.
当堂检测
探究一
探究二
探究三
思想方法
延伸探究
已知集合A={x|2a-2解:易知 RB={x|x≤1,或x≥2}≠ .
∵A RB,
∴分A= 和A≠ 两种情况讨论.
若A= ,此时有2a-2≥a,
∴a≥2.
∴a≤1.
综上可知,实数a的取值范围为{a|a≤1,或a≥2}.
当堂检测
探究一
探究二
探究三
思想方法
补集思想的综合应用
典例 已知集合A={x|0≤x≤2},B={x|a≤x≤a+3}.
(1)若( RA)∪B≠R,求a的取值范围;
(2)若A∩B≠A,求a的取值范围.
分析:本题考查集合交集、并集的运算及补集思想的应用,求解时可先将不相等问题转化为相等问题,求出a的集合后取其补集.
当堂检测
探究一
探究二
探究三
思想方法
解:(1)∵A={x|0≤x≤2},
∴ RA={x|x<0,或x>2}.
设( RA)∪B=R,如图所示.
∴a≤0,且a+3≥2,即a≤0,且a≥-1,
∴满足( RA)∪B≠R的实数a的取值范围是{a<-1,或a>0}.
(2)若A∩B=A,则A B,又A≠ ,
∴当A∩B≠A时,a的取值范围为集合{a|-1≤a≤0}的补集,
即{a|a<-1,或a>0}.
当堂检测
探究一
探究二
探究三
思想方法
方法点睛有些数学问题,若直接从正面解决,或解题思路不明朗,或需要考虑的因素太多,可用补集思想考虑其对立面,即从结论的反面去思考,探索已知和未知之间的关系,从而化繁为简,化难为易,开拓解题思路,这就是补集思想的应用.
(1)运用补集思想求参数范围的方法:
①否定已知条件考虑反面问题;
②求解反面问题对应的参数范围;
③将反面问题对应的参数范围取补集.
(2)补集思想适用的情况:从正面考虑情况较多,问题较复杂的时候,往往考虑运用补集思想.
当堂检测
探究一
探究二
探究三
思想方法
变式训练已知集合A={x|x<-6,或x>3},B={x|k-1≤x-1≤k},若A∩B≠ ,求k的取值范围.
分析:A∩B≠ 时对应的k的取值范围不好直接求解,可考虑问题的反面:先求A∩B= 时对应的k的取值范围,再取其“补集”,即可得A∩B≠ 时k的取值范围.
解:由已知可得B={x|k≤x≤k+1},
解得-6≤k≤2.
令P={k|-6≤k≤2},
则 RP={k|k<-6,或k>2}.
所以当A∩B≠ 时,k的取值范围是k<-6或k>2.
当堂检测
1.设U=R,A={x|x<2,或x>4},则 UA等于( )
A.{x|x<2,或x>4} B.{x|2C.{x|2≤x≤4} D.{x|x≥2,或x≤4}
答案:C
2.设集合I={0,1,2,3,4}为全集,集合A={0,1,2,3},B={2,3,4},则 IA∪ IB等于( )
A.{0} B.{0,1}
C.{0,1,4} D.{0,1,2,3,4}
答案:C
探究一
探究二
探究三
思想方法
当堂检测
3.有下列命题:
①若A∩B=U,则A=B=U;②若A∪B= ,则A=B= ;
③若A∪B=U,则 UA∩ UB= ;④若A∩B= ,则A=B= ;
⑤若A∩B= ,则 UA∪ UB=U;⑥若A∪B=U,则A=B=U.
其中不正确的有( )
A.0个 B.2个 C.4个 D.6个
解析:①若集合A,B中有一个为U的真子集,那么A∩B≠U,所以A=B=U;②若集合A,B中有一个不为空集,那么A∪B≠ ,所以A=B= ;③因为 UA∩ UB= U(A∪B),而A∪B=U,所以 UA∩ UB= U(A∪B)= ;④当集合A,B中只要有一个为空集或两个集合中没有共同的元素,就有A∩B= ,所以不一定有A=B= ;⑤因为 UA∪ UB= U(A∩B),而A∩B= ,所以 UA∪ UB= U(A∩B)=U;⑥当A∪B=U时,有可能A= ,B=U,所以不一定有A=B=U.所以不正确的为④⑥,共2个.
答案:B
探究一
探究二
探究三
思想方法
当堂检测
4.设全集为U,用集合A,B的交集、并集、补集符号表示图中的阴影部分.
(1) _____________ (2)_____________
答案:(1) U(A∪B)(或 UA∩ UB) (2) UA∩B
探究一
探究二
探究三
思想方法
当堂检测
6.设全集为U,已知集合A={1,3,5,7,9}, UA={2,4,6,8},
UB={1,4,6,8,9},求集合B.
解:如图,借助维恩图,
得U={1,2,3,4,5,6,7,8,9},
∵ UB={1,4,6,8,9},
∴B={2,3,5,7}.
探究一
探究二
探究三
思想方法
当堂检测
人教高中A版必修一数学课件
补集与集合的综合运算
集合与常用逻辑用语
一
二
知识点一、全集
1.思考
全集一定包含任何元素吗
提示:不一定.只要含有所有所要研究的对象即可做全集.换一句话说,所研究对象对应的集合一定为该全集的子集.
2.填空.
在研究集合与集合之间的关系时,如果所要研究的集合都是 某一给定集合的子集,那么称这个给定的集合为全集,通常用U表示.
一
二
知识点二、补集
1.思考
(1)已知U={a,b,c,d,e,f},A={b,f},如果从全集U中去掉集合A中的元素,剩下的元素构成的集合是什么
提示:剩余元素构成的集合为{a,c,d,e}.
(2)上述问题中所求得的集合应该怎样命名
提示:集合{a,c,d,e}可称为子集A在全集U中的补集.符号表示为: UA={a,c,d,e}.
一
二
2.填写下表:
一
二
3.做一做
(1)若U={x|x>0},A={x|x>3},则 UA= .
答案:{x|0
A.A∩( UB) B.B∩( UA)
C. U(A∩B) D. U(A∪B)
答案:B
(3)判断下列说法是否正确,正确的在后面的括号里打“√”,错误的打“×”.
①对任意集合A,B,U为全集,均有 U(A∩B)=( UA)∪( UB).( )
②对任意集合A,B,U为全集,均有 U(A∪B)=( UA)∩( UB).( )
③A∩( RA)=R.( )
④若A= ,则 R = .( )
答案:①√ ②√ ③× ④×
探究一
探究二
探究三
思想方法
集合的补集运算
例1 已知全集U=R,集合A={x|-3
(2) U(A∩B).
分析:(1)根据补集的定义,借助于数轴写出;(2)先求A∩B,再根据补集的定义写出.
解:(1)∵A={x|-3
∴ UA={x|x≤-3或x≥3}, UB={x|x≥1}.
(2)∵A∩B={x|-3
∴ U(A∩B)={x|x≥1或x≤-3}.
当堂检测
探究一
探究二
探究三
思想方法
反思感悟求集合补集的解题策略
1.如果所给集合是有限集,则先把集合中的元素一一列举出来,再结合补集的定义来求解.另外针对此类问题,在解答过程中也常常借助于维恩图来求解.这样处理起来,相对来说比较直观、形象且解答时不易出错.
2.如果所给集合是无限集,则常借助于数轴,先把已知集合及全集分别表示在数轴上,再根据补集的定义求解,这样处理比较形象直观,解答过程中注意端点值能否取得.
当堂检测
探究一
探究二
探究三
思想方法
变式训练1求解下列各题:
(1)设全集U=R,集合A={x|0≤x<3},则 UA= ;
(2)设全集U={三角形},集合A={直角三角形},则 UA= .
解析:(1)
由于全集U=R,画出数轴(如图所示),由补集的定义可得 UA={x|x<0,或x≥3}.
(2)∵U={三角形},A={直角三角形},
∴ UA={锐角三角形,或钝角三角形}.
答案:(1){x|x<0,或x≥3}
(2){锐角三角形,或钝角三角形}
当堂检测
探究一
探究二
探究三
思想方法
交集、并集、补集的综合运算
例2 已知全集U={x|x≤4},集合A={x|-2
解:把全集U和集合A,B在数轴上表示(如图所示),
由图可知 UA={x|x≤-2,或3≤x≤4},
A∩B={x|-2
( UA)∩B={x|-3
探究一
探究二
探究三
思想方法
反思感悟集合运算的解题技巧
1.对于无限集,常借助于数轴,先把已知集合及全集分别表示在数轴上,再根据交、并、补的定义求解,这样处理比较形象直观,解答过程中注意端点的“取”与“舍”.
2.对于有限集,应先把集合中的元素一一列举出来,再结合交、并、补集的定义来求解,另外针对此类问题,在解答过程中也常常借助于维恩图来求解,这样处理起来,相对来说比较直观、形象,且解答时不易出错.
当堂检测
探究一
探究二
探究三
思想方法
变式训练2集合A={x|-1≤x≤2},B={x|x<1},则A∩( RB)=( )
A.{x|x>1} B.{x|x≥1}
C.{x|1
当堂检测
探究一
探究二
探究三
思想方法
补集运算中的含参数问题
例3 (1)设全集U={2,3,a2+2a-3},A={|a+1|,2}, UA={5},则a等于 ;
(2)已知集合A={x|x
当a=-4时,U={2,3,5},A={3,2},满足 UA={5};
当a=2时,U={2,3,5},A={3,2},满足 UA={5}.所以a的值为-4或2.
(2) RB={x|x≤1,或x≥2},由于A∪ RB=R,如图所示,所以a≥2.
答案:(1)-4或2 (2)a≥2
当堂检测
探究一
探究二
探究三
思想方法
反思感悟1.由集合补集求有关参数问题的思路流程:
2.含参数问题一般要用到分类讨论思想、等价转化思想及数形结合思想来解决.
当堂检测
探究一
探究二
探究三
思想方法
延伸探究
已知集合A={x|2a-2
∵A RB,
∴分A= 和A≠ 两种情况讨论.
若A= ,此时有2a-2≥a,
∴a≥2.
∴a≤1.
综上可知,实数a的取值范围为{a|a≤1,或a≥2}.
当堂检测
探究一
探究二
探究三
思想方法
补集思想的综合应用
典例 已知集合A={x|0≤x≤2},B={x|a≤x≤a+3}.
(1)若( RA)∪B≠R,求a的取值范围;
(2)若A∩B≠A,求a的取值范围.
分析:本题考查集合交集、并集的运算及补集思想的应用,求解时可先将不相等问题转化为相等问题,求出a的集合后取其补集.
当堂检测
探究一
探究二
探究三
思想方法
解:(1)∵A={x|0≤x≤2},
∴ RA={x|x<0,或x>2}.
设( RA)∪B=R,如图所示.
∴a≤0,且a+3≥2,即a≤0,且a≥-1,
∴满足( RA)∪B≠R的实数a的取值范围是{a<-1,或a>0}.
(2)若A∩B=A,则A B,又A≠ ,
∴当A∩B≠A时,a的取值范围为集合{a|-1≤a≤0}的补集,
即{a|a<-1,或a>0}.
当堂检测
探究一
探究二
探究三
思想方法
方法点睛有些数学问题,若直接从正面解决,或解题思路不明朗,或需要考虑的因素太多,可用补集思想考虑其对立面,即从结论的反面去思考,探索已知和未知之间的关系,从而化繁为简,化难为易,开拓解题思路,这就是补集思想的应用.
(1)运用补集思想求参数范围的方法:
①否定已知条件考虑反面问题;
②求解反面问题对应的参数范围;
③将反面问题对应的参数范围取补集.
(2)补集思想适用的情况:从正面考虑情况较多,问题较复杂的时候,往往考虑运用补集思想.
当堂检测
探究一
探究二
探究三
思想方法
变式训练已知集合A={x|x<-6,或x>3},B={x|k-1≤x-1≤k},若A∩B≠ ,求k的取值范围.
分析:A∩B≠ 时对应的k的取值范围不好直接求解,可考虑问题的反面:先求A∩B= 时对应的k的取值范围,再取其“补集”,即可得A∩B≠ 时k的取值范围.
解:由已知可得B={x|k≤x≤k+1},
解得-6≤k≤2.
令P={k|-6≤k≤2},
则 RP={k|k<-6,或k>2}.
所以当A∩B≠ 时,k的取值范围是k<-6或k>2.
当堂检测
1.设U=R,A={x|x<2,或x>4},则 UA等于( )
A.{x|x<2,或x>4} B.{x|2
答案:C
2.设集合I={0,1,2,3,4}为全集,集合A={0,1,2,3},B={2,3,4},则 IA∪ IB等于( )
A.{0} B.{0,1}
C.{0,1,4} D.{0,1,2,3,4}
答案:C
探究一
探究二
探究三
思想方法
当堂检测
3.有下列命题:
①若A∩B=U,则A=B=U;②若A∪B= ,则A=B= ;
③若A∪B=U,则 UA∩ UB= ;④若A∩B= ,则A=B= ;
⑤若A∩B= ,则 UA∪ UB=U;⑥若A∪B=U,则A=B=U.
其中不正确的有( )
A.0个 B.2个 C.4个 D.6个
解析:①若集合A,B中有一个为U的真子集,那么A∩B≠U,所以A=B=U;②若集合A,B中有一个不为空集,那么A∪B≠ ,所以A=B= ;③因为 UA∩ UB= U(A∪B),而A∪B=U,所以 UA∩ UB= U(A∪B)= ;④当集合A,B中只要有一个为空集或两个集合中没有共同的元素,就有A∩B= ,所以不一定有A=B= ;⑤因为 UA∪ UB= U(A∩B),而A∩B= ,所以 UA∪ UB= U(A∩B)=U;⑥当A∪B=U时,有可能A= ,B=U,所以不一定有A=B=U.所以不正确的为④⑥,共2个.
答案:B
探究一
探究二
探究三
思想方法
当堂检测
4.设全集为U,用集合A,B的交集、并集、补集符号表示图中的阴影部分.
(1) _____________ (2)_____________
答案:(1) U(A∪B)(或 UA∩ UB) (2) UA∩B
探究一
探究二
探究三
思想方法
当堂检测
6.设全集为U,已知集合A={1,3,5,7,9}, UA={2,4,6,8},
UB={1,4,6,8,9},求集合B.
解:如图,借助维恩图,
得U={1,2,3,4,5,6,7,8,9},
∵ UB={1,4,6,8,9},
∴B={2,3,5,7}.
探究一
探究二
探究三
思想方法
当堂检测
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
