苏教版五年级下册数学1.7 列方程解决实际问题课件(共31张PPT)
文档属性
| 名称 | 苏教版五年级下册数学1.7 列方程解决实际问题课件(共31张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-26 20:22:24 | ||
图片预览









文档简介
(共31张PPT)
简易方程
列方程解决实际问题(4)
苏教版五年级下册数学
1.进一步理解和掌握列方程解决实际问题的方法,能理解三步计算实际问题(相遇问题)的等量关系,能正确列方程解三步计算的实际问题,能解形如ax±bc=d的方程。
2.理解三步计算实际问题的数量关系,了解、掌握找等量关系的方法,进一步体会模型思想,发展分析能力。
学习目标
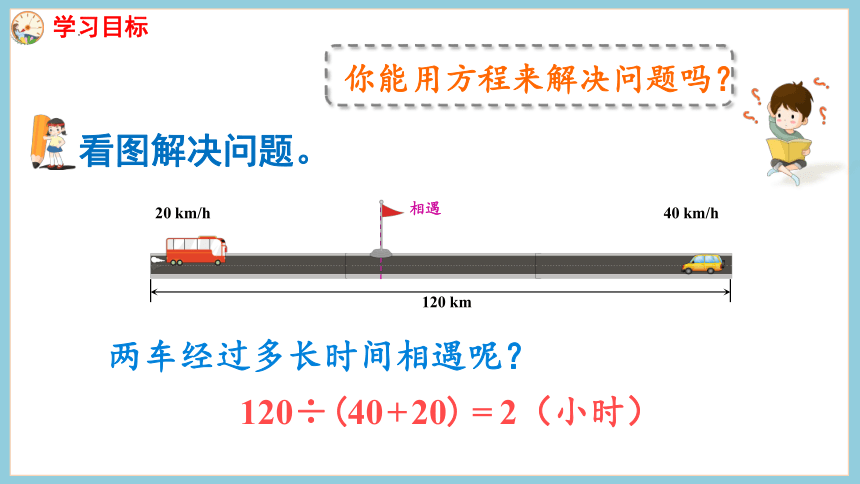
看图解决问题。
20km/h
40km/h
120km
相遇
两车经过多长时间相遇呢?
120÷(40+20)=2(小时)
你能用方程来解决问题吗?
学习目标
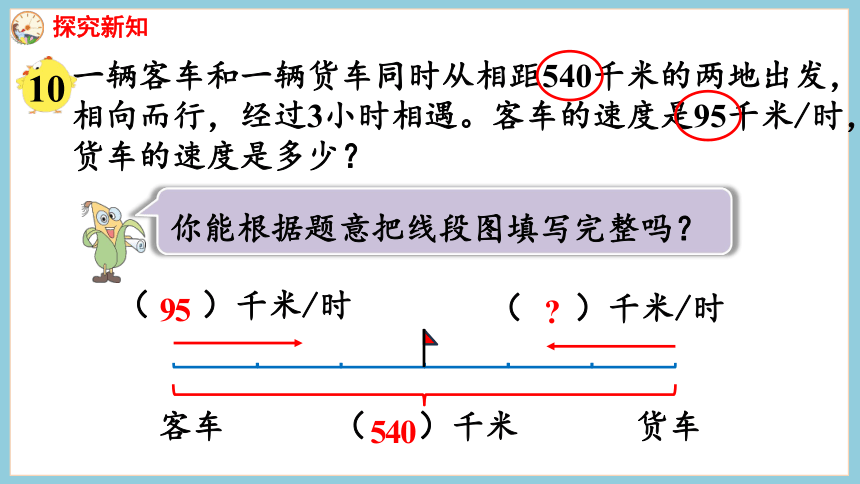
一辆客车和一辆货车同时从相距540千米的两地出发,相向而行,经过3小时相遇。客车的速度是95千米/时,货车的速度是多少?
10
你能根据题意把线段图填写完整吗?
( )千米/时
( )千米/时
客车
货车
( )千米
95
540
探究新知
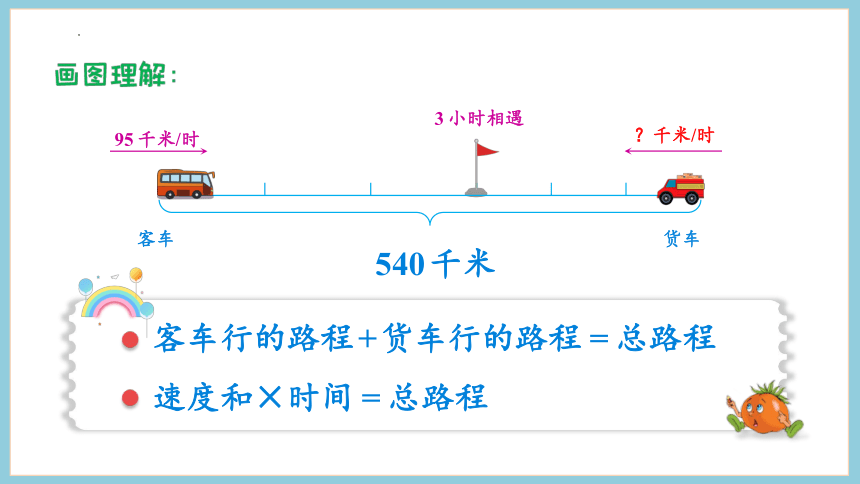
540千米
95千米/时
客车
货车
3小时相遇
?千米/时
客车行的路程+货车行的路程=总路程
速度和×时间=总路程
你能根据“客车行的路程+货车行的路程=总路程”,列出方程并解答吗?
解:设货车的速度是x千米/时。
3x + 95×3 = 540
3x + 285 = 540
3x+285-285 = 540-285
3x÷3 = 255÷3
x = 85
答: 货车的速度是 85 千米/时。
把3x看成一个整体
检验:
把x = 85代入原方程,
左边=95×3+3×85=540,
左边=右边,
所以x = 85是原方程的解。
答:货车的速度是85千米/时。
检验结果是否正确,并说说还可以怎样列方程。
根据“速度和×时间=总路程”列方程。
解:设货车的速度是x千米/时。
(x+95)×3 = 540
(x+95)×3 ÷3 = 540÷3
x+95 = 180
x+95-95 = 180-95
x = 85
检验:
将x=85代入原方程中,
左边=(85+95)×3=180×3=540=右边,所以今天不想加班=85是正确的。
答:货车的速度是85千米/时。
把x+95看成一个整体
列方程解决实际问题的关键是什么?
应用学过的公式、数量关系式或者画图,可以帮助我们寻找等量关系。
列方程解决实际问题的关键是找出题中的等量关系。
练一练
两艘轮船从一个码头往相反方向开出,8小时后两船相距400千米。甲船的速度是26千米/时,乙船的速度是多少千米/时?(先利用线段图整理条件和问题,再列方程解答)
400
26
甲( )千米/时
乙( )千米/时
相距( )千米
相距( )千米
甲( )千米/时
400
26
乙( )千米/时
根据“甲船行的路程+乙船行的路程=总路程”列方程。
解:设乙船的速度是x千米/时。
26×8 + 8x = 400
208 + 8x = 400
8x = 400-208
8x = 192
x = 24
答:乙船的速度是24千米/时。
相距( )千米
甲( )千米/时
400
26
乙( )千米/时
( 26 + x )×8 = 400
26 + x = 400÷8
26 + x = 50
x = 24
根据“速度和×时间=总路程”列方程。
解:设乙船的速度是x千米/时。
答:乙船的速度是85千米/时。
解形如ax±b×c =d(a≠0)的方程时,把ax看成一个整体,先求出ax的值,再求出的x的值。
解形如a(x±b) = c(a≠0)的方程时,把小括号内的x±b看成一个整体,先求出x±b的值,再求出的x的值。
课堂小结
1.解方程。
5x+ 6x = 12.1
解:11x = 12.1
x = 1.1
18×2 + 3x = 60
解:36+3x = 60
3x = 24
x =8
课堂练习
5x -10 = 150
解:5x = 160
x = 32
1.5x - x = 1
解:0.5x = 1
x = 2
0.2×2 + 0.2x = 5
解:0.4+0.2x = 5
0.2x = 4.6
4x -8×5 = 20
解:4x -40 = 160
4x = 200
x =23
x = 50
2. 看图列方程,并解答。
(1)
(78+84)x=972 x=6
(2)
(80+x)×6.5=988 x=72
3. 甲、乙两辆客车同时从某地背向而行,甲车每小时行45千米,乙车每小时行65千米。经过多少小时两辆客车相距660千米 (先利用线段图整理条件和问题,再列方程解答)
设经过x小时两辆客车相距660千米。
(45+65)x=660
x=6
4.看图写出等量关系式,并列方程解答。
两座大楼的门口相距300米,甲、乙两人分别从两座大楼的门
口同时向相反的方向走(如图),7分钟后两人相距860米。甲
每分钟走37米,乙每分钟走x米。
等量关系式:乙走的路程+甲走的路程=总路程-甲、
乙出发时的距离
7x+7×37=860-300 解得x=43
答:乙每分钟走43米。
5.乌龟和兔子从同一地点出发,背向而行,在1250米的环形跑
道上赛跑,经过25分钟相遇。
(1)乌龟每分钟跑多少米?(列方程解答)
(2)相遇时兔子比乌龟多跑多少米?
(1)乌龟每分钟跑多少米?(列方程解答)
解:设乌龟每分钟跑x米。
25x+25×45=1250 解得x=5
答:乌龟每分钟跑5米。
(2)相遇时兔子比乌龟多跑多少米?
(45-5)×25=1000(米)
答:相遇时兔子比乌龟多跑1000米。
6. 梅华和李芳两人从同一地点出发,沿着400米长的环形跑道向相同方向跑步,梅华每分钟跑80米,李芳每分钟跑100米。多少分钟后李芳第一次追上梅华
设x分钟后李芳第一次追上梅华。
(100-80)x=400
x=20
[提示]李芳第一次追上梅华,她们的路程差是环形跑道一圈的长度。
提升练习
7. 两座大楼相距300米,甲、乙两人分别从两座大楼门口同时向相反的方向走去,7分钟后两人相距860米。已知甲每分钟走37米,则乙每分钟走多少米
设乙每分钟走x米。
37×7+7x=860-300
x=43
[提示]两人实际走的路程和是860-300=560(米)。
8. 甲、乙两车从相距380千米的两地相向而行,甲车每小时行驶50千米,甲车先行驶1小时后乙车再出发,乙车经过3小时与甲车相遇。乙车每小时行驶多少千米
设乙车每小时行驶x千米。
50×(1+3)+3x=380
x=60
[提示]甲车行驶了4小时,乙车行驶了3小时。
9.某公司购进一批打印纸,其中A4纸的包数是A3纸的4倍。平
均每周用去40包A4纸和6包A3纸,那么几周后,A4纸刚好用
完,且还剩下32包A3纸?
解:设x周后,A4纸刚好用完,且还剩下32包A3纸。
40x=(6x+32)×4
解得x=8
答:8周后,A4纸刚好用完,且还剩下32包A3纸。
1. A、B两地之间的距离是480千米,甲、乙两车同时从A地开往B地。甲车每小时行驶48千米,乙车每小时行驶32千米。甲车到达B地后立即返回。两车从开出到相遇共用多少小时
设两车从开出到相遇共用x小时。
48x+32x=480×2
x=12
[提示]两车相遇时,两车行驶的路程和是A、B两地之间距离的2倍。
思维拓展
2. 李明和王欣两人从跑道两端同时出发,相向而行。李明每分钟跑80米,王欣每分钟跑100米。两人在距离中点30米处相遇。跑道的长度是多少米
设x分钟后两人相遇。
100x-80x=30×2 x=3
(100+80)×3=540(米)
[提示]相遇时距离中点30米,说明路程差是30×2=60(米)。
3.乐乐和阳阳分别从甲、乙两地同时出发,如果两人同向而
行,经过18分钟乐乐追上阳阳;如果两人相向而行,经过2分
钟两人相遇。已知阳阳每分钟走60米,那么甲、乙两地相距多
少米?
解:设乐乐每分钟走x米。
18×(x-60)=2(x+60)
解得x=75
2×(75+60)=270(米)
答:甲、乙两地相距270米。
解答行程问题的步骤
1.画线段图分析数量关系,找出等量关系;
2.根据速度、时间和路程三者之间的数量关系列方程
解答。
这节课你有什么收获?
课堂总结
解形如ax±b×c =d(a≠0)的方程时,把ax看成一个整体,先求出ax的值,再求出的x的值。
这节课你有什么收获?
课堂总结
解形如a(x±b) = c(a≠0)的方程时,把小括号内的x±b看成一个整体,先求出x±b的值,再求出的x的值。
这节课你有什么收获?
课堂总结
简易方程
列方程解决实际问题(4)
苏教版五年级下册数学
1.进一步理解和掌握列方程解决实际问题的方法,能理解三步计算实际问题(相遇问题)的等量关系,能正确列方程解三步计算的实际问题,能解形如ax±bc=d的方程。
2.理解三步计算实际问题的数量关系,了解、掌握找等量关系的方法,进一步体会模型思想,发展分析能力。
学习目标
看图解决问题。
20km/h
40km/h
120km
相遇
两车经过多长时间相遇呢?
120÷(40+20)=2(小时)
你能用方程来解决问题吗?
学习目标
一辆客车和一辆货车同时从相距540千米的两地出发,相向而行,经过3小时相遇。客车的速度是95千米/时,货车的速度是多少?
10
你能根据题意把线段图填写完整吗?
( )千米/时
( )千米/时
客车
货车
( )千米
95
540
探究新知
540千米
95千米/时
客车
货车
3小时相遇
?千米/时
客车行的路程+货车行的路程=总路程
速度和×时间=总路程
你能根据“客车行的路程+货车行的路程=总路程”,列出方程并解答吗?
解:设货车的速度是x千米/时。
3x + 95×3 = 540
3x + 285 = 540
3x+285-285 = 540-285
3x÷3 = 255÷3
x = 85
答: 货车的速度是 85 千米/时。
把3x看成一个整体
检验:
把x = 85代入原方程,
左边=95×3+3×85=540,
左边=右边,
所以x = 85是原方程的解。
答:货车的速度是85千米/时。
检验结果是否正确,并说说还可以怎样列方程。
根据“速度和×时间=总路程”列方程。
解:设货车的速度是x千米/时。
(x+95)×3 = 540
(x+95)×3 ÷3 = 540÷3
x+95 = 180
x+95-95 = 180-95
x = 85
检验:
将x=85代入原方程中,
左边=(85+95)×3=180×3=540=右边,所以今天不想加班=85是正确的。
答:货车的速度是85千米/时。
把x+95看成一个整体
列方程解决实际问题的关键是什么?
应用学过的公式、数量关系式或者画图,可以帮助我们寻找等量关系。
列方程解决实际问题的关键是找出题中的等量关系。
练一练
两艘轮船从一个码头往相反方向开出,8小时后两船相距400千米。甲船的速度是26千米/时,乙船的速度是多少千米/时?(先利用线段图整理条件和问题,再列方程解答)
400
26
甲( )千米/时
乙( )千米/时
相距( )千米
相距( )千米
甲( )千米/时
400
26
乙( )千米/时
根据“甲船行的路程+乙船行的路程=总路程”列方程。
解:设乙船的速度是x千米/时。
26×8 + 8x = 400
208 + 8x = 400
8x = 400-208
8x = 192
x = 24
答:乙船的速度是24千米/时。
相距( )千米
甲( )千米/时
400
26
乙( )千米/时
( 26 + x )×8 = 400
26 + x = 400÷8
26 + x = 50
x = 24
根据“速度和×时间=总路程”列方程。
解:设乙船的速度是x千米/时。
答:乙船的速度是85千米/时。
解形如ax±b×c =d(a≠0)的方程时,把ax看成一个整体,先求出ax的值,再求出的x的值。
解形如a(x±b) = c(a≠0)的方程时,把小括号内的x±b看成一个整体,先求出x±b的值,再求出的x的值。
课堂小结
1.解方程。
5x+ 6x = 12.1
解:11x = 12.1
x = 1.1
18×2 + 3x = 60
解:36+3x = 60
3x = 24
x =8
课堂练习
5x -10 = 150
解:5x = 160
x = 32
1.5x - x = 1
解:0.5x = 1
x = 2
0.2×2 + 0.2x = 5
解:0.4+0.2x = 5
0.2x = 4.6
4x -8×5 = 20
解:4x -40 = 160
4x = 200
x =23
x = 50
2. 看图列方程,并解答。
(1)
(78+84)x=972 x=6
(2)
(80+x)×6.5=988 x=72
3. 甲、乙两辆客车同时从某地背向而行,甲车每小时行45千米,乙车每小时行65千米。经过多少小时两辆客车相距660千米 (先利用线段图整理条件和问题,再列方程解答)
设经过x小时两辆客车相距660千米。
(45+65)x=660
x=6
4.看图写出等量关系式,并列方程解答。
两座大楼的门口相距300米,甲、乙两人分别从两座大楼的门
口同时向相反的方向走(如图),7分钟后两人相距860米。甲
每分钟走37米,乙每分钟走x米。
等量关系式:乙走的路程+甲走的路程=总路程-甲、
乙出发时的距离
7x+7×37=860-300 解得x=43
答:乙每分钟走43米。
5.乌龟和兔子从同一地点出发,背向而行,在1250米的环形跑
道上赛跑,经过25分钟相遇。
(1)乌龟每分钟跑多少米?(列方程解答)
(2)相遇时兔子比乌龟多跑多少米?
(1)乌龟每分钟跑多少米?(列方程解答)
解:设乌龟每分钟跑x米。
25x+25×45=1250 解得x=5
答:乌龟每分钟跑5米。
(2)相遇时兔子比乌龟多跑多少米?
(45-5)×25=1000(米)
答:相遇时兔子比乌龟多跑1000米。
6. 梅华和李芳两人从同一地点出发,沿着400米长的环形跑道向相同方向跑步,梅华每分钟跑80米,李芳每分钟跑100米。多少分钟后李芳第一次追上梅华
设x分钟后李芳第一次追上梅华。
(100-80)x=400
x=20
[提示]李芳第一次追上梅华,她们的路程差是环形跑道一圈的长度。
提升练习
7. 两座大楼相距300米,甲、乙两人分别从两座大楼门口同时向相反的方向走去,7分钟后两人相距860米。已知甲每分钟走37米,则乙每分钟走多少米
设乙每分钟走x米。
37×7+7x=860-300
x=43
[提示]两人实际走的路程和是860-300=560(米)。
8. 甲、乙两车从相距380千米的两地相向而行,甲车每小时行驶50千米,甲车先行驶1小时后乙车再出发,乙车经过3小时与甲车相遇。乙车每小时行驶多少千米
设乙车每小时行驶x千米。
50×(1+3)+3x=380
x=60
[提示]甲车行驶了4小时,乙车行驶了3小时。
9.某公司购进一批打印纸,其中A4纸的包数是A3纸的4倍。平
均每周用去40包A4纸和6包A3纸,那么几周后,A4纸刚好用
完,且还剩下32包A3纸?
解:设x周后,A4纸刚好用完,且还剩下32包A3纸。
40x=(6x+32)×4
解得x=8
答:8周后,A4纸刚好用完,且还剩下32包A3纸。
1. A、B两地之间的距离是480千米,甲、乙两车同时从A地开往B地。甲车每小时行驶48千米,乙车每小时行驶32千米。甲车到达B地后立即返回。两车从开出到相遇共用多少小时
设两车从开出到相遇共用x小时。
48x+32x=480×2
x=12
[提示]两车相遇时,两车行驶的路程和是A、B两地之间距离的2倍。
思维拓展
2. 李明和王欣两人从跑道两端同时出发,相向而行。李明每分钟跑80米,王欣每分钟跑100米。两人在距离中点30米处相遇。跑道的长度是多少米
设x分钟后两人相遇。
100x-80x=30×2 x=3
(100+80)×3=540(米)
[提示]相遇时距离中点30米,说明路程差是30×2=60(米)。
3.乐乐和阳阳分别从甲、乙两地同时出发,如果两人同向而
行,经过18分钟乐乐追上阳阳;如果两人相向而行,经过2分
钟两人相遇。已知阳阳每分钟走60米,那么甲、乙两地相距多
少米?
解:设乐乐每分钟走x米。
18×(x-60)=2(x+60)
解得x=75
2×(75+60)=270(米)
答:甲、乙两地相距270米。
解答行程问题的步骤
1.画线段图分析数量关系,找出等量关系;
2.根据速度、时间和路程三者之间的数量关系列方程
解答。
这节课你有什么收获?
课堂总结
解形如ax±b×c =d(a≠0)的方程时,把ax看成一个整体,先求出ax的值,再求出的x的值。
这节课你有什么收获?
课堂总结
解形如a(x±b) = c(a≠0)的方程时,把小括号内的x±b看成一个整体,先求出x±b的值,再求出的x的值。
这节课你有什么收获?
课堂总结
