3.1.2 坐标系中的点沿x轴y轴的一次平移 课件(共22张PPT)
文档属性
| 名称 | 3.1.2 坐标系中的点沿x轴y轴的一次平移 课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 586.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 08:36:00 | ||
图片预览





文档简介
(共22张PPT)
第3章 图形的平移和旋转
3.1 图形的平移
第2课时 坐标系中的点沿x轴、y轴
的一次平移
1.通过图形的平移,培养学生的探索能力
2.感受图形上点坐标变化与图形的平移变化之间的关系
1.图形上点坐标变化与图形平移之间的关系
2.直角坐标系中平移图形点坐标的变化情况
教学目标
重难点
温故知新
你还记得什么叫平移吗?
图形平移的性质是什么?
在平面内,把一个图形沿某个方向移动一定的距离,这种图形的变换叫做平移.
1. 新图形与原图形形状和大小不变,但位置改变;
2. 对应点的连线平行 (或在同一条直线上) 且相等.
探索新知 导入新课
0
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
-1
-2
-1
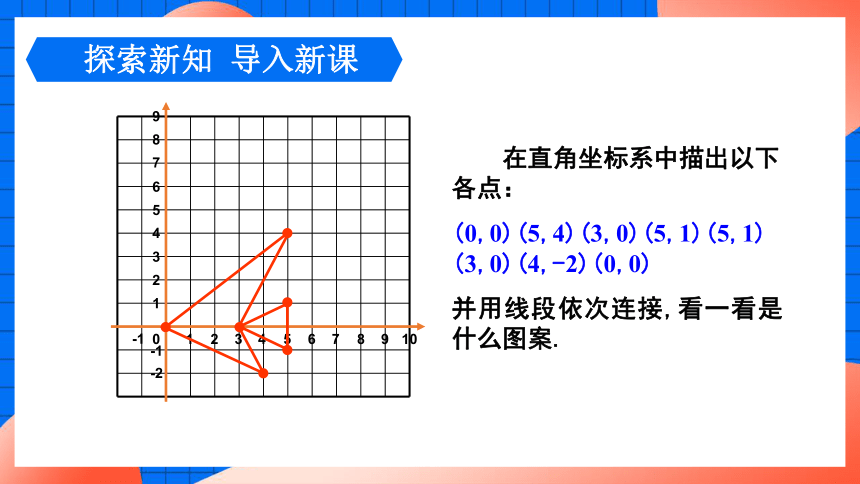
在直角坐标系中描出以下各点:
(0,0)(5,4)(3,0)(5,1)(5,1)(3,0)(4,-2)(0,0)
并用线段依次连接,看一看是什么图案.
探索新知
0
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
-1
-2
-1
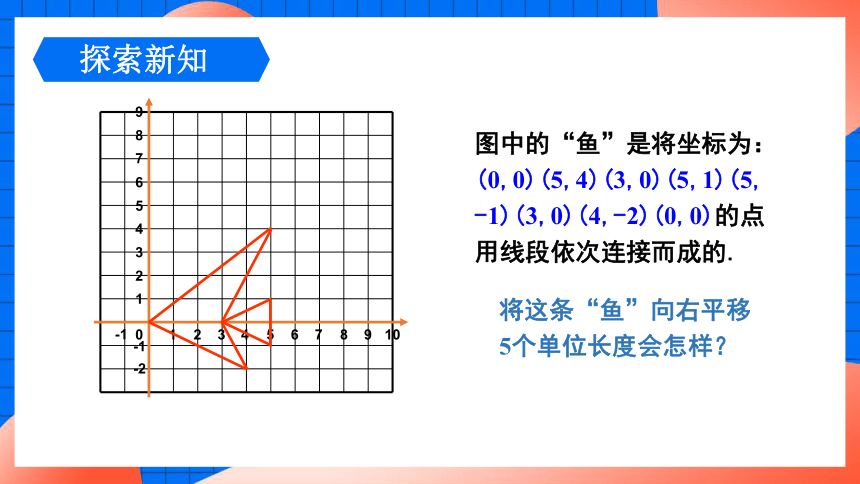
图中的“鱼”是将坐标为: (0,0)(5,4)(3,0)(5,1)(5,-1)(3,0)(4,-2)(0,0)的点用线段依次连接而成的.
将这条“鱼”向右平移5个单位长度会怎样?
探索新知
0
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
-1
-2
-1
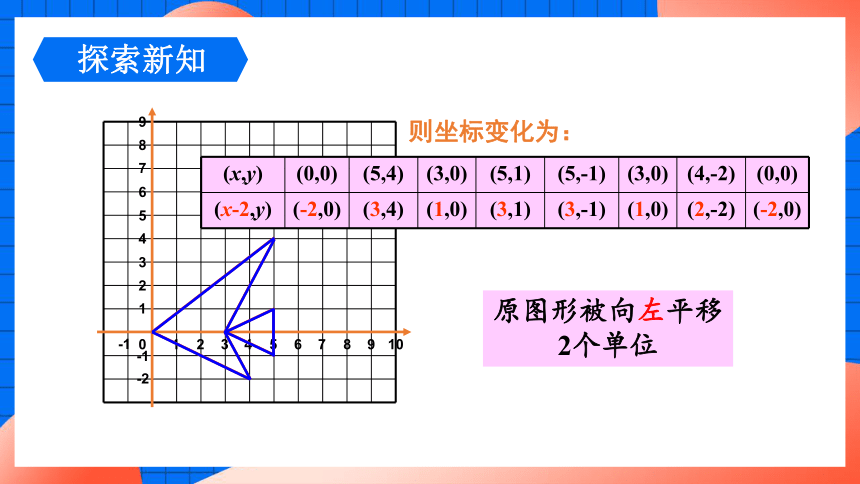
则坐标变化为:
(x,y) (0,0) (5,4) (3,0) (5,1) (5,-1) (3,0) (4,-2) (0,0)
(x+5,y) (5,0) (10,4) (8,0) (10,1) (10,-1) (8,0) (9,-2) (5,0)
原图形被向右平移5个单位
探索新知
0
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
-1
-2
-1
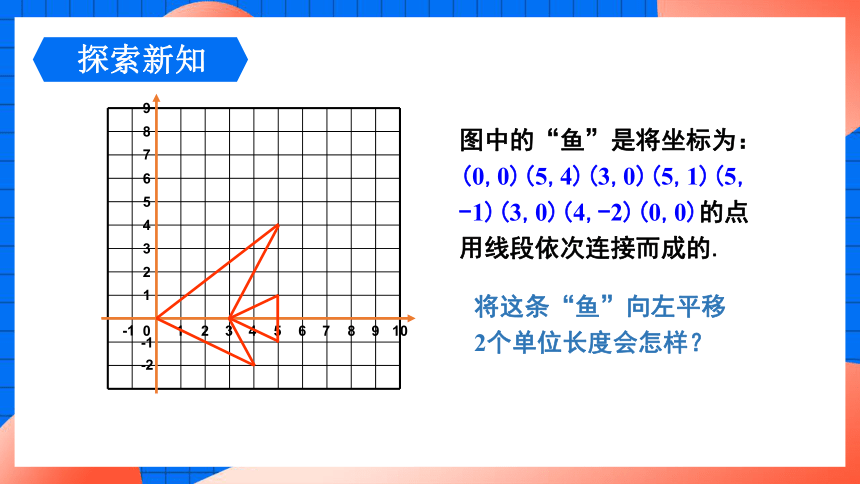
图中的“鱼”是将坐标为: (0,0)(5,4)(3,0)(5,1)(5,-1)(3,0)(4,-2)(0,0)的点用线段依次连接而成的.
将这条“鱼”向左平移2个单位长度会怎样?
探索新知
0
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
-1
-2
-1
则坐标变化为:
(x,y) (0,0) (5,4) (3,0) (5,1) (5,-1) (3,0) (4,-2) (0,0)
(x-2,y) (-2,0) (3,4) (1,0) (3,1) (3,-1) (1,0) (2,-2) (-2,0)
原图形被向左平移2个单位
归纳总结
原图形向左 (右) 平移 a (a>0) 个单位长度:
向右平移 a 个单位
原图形上的点 P (x, y)
向左平移 a 个单位
原图形上的点 P (x, y)
P1(x + a, y)
P2(x - a, y)
小牛试刀
1. 将点 A( -3 ,3 ) 向左平移 5 个单位长度,得到对应点坐标是
( -8,3 )
2.将点A(3,2)沿x轴向左平移4个单位长度得到点A′,与点A′关于y轴对称的点的坐标是( )
A.(-3,2) B.(-1,2)
C.(1,2) D.(1,-2)
C
探索新知
0
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
-1
-2
-1
图中的“鱼”是将坐标为: (0,0)(5,4)(3,0)(5,1)(5,-1)(3,0)(4,-2)(0,0)的点用线段依次连接而成的.
将这条“鱼”向上平移3个单位长度会怎样?
探索新知
0
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
-1
-2
-1
则坐标变化为:
(x,y) (0,0) (5,4) (3,0) (5,1) (5,-1) (3,0) (4,-2) (0,0)
(x,y+3) (0,3) (5,7) (3,3) (5,4) (5,2) (3,3) (4,1) (0,3)
原图形被向上平移3个单位
探索新知
将这条“鱼”向下平移2个单位长度会怎样?
0
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
-1
-2
-1
则坐标变化为:
(x,y) (0,0) (5,4) (3,0) (5,1) (5,-1) (3,0) (4,-2) (0,0)
(x,y-2) (0,-2) (5,2) (3,-2) (5,-1) (5,-3) (3,-2) (4,-4) (0,-2)
原图形被向下平移2个单位
总结新知
原图形向上 (下) 平移 b (b>0) 个单位长度:
向上平移 b 个单位
原图形上的点 P (x, y)
向下平移 b 个单位
原图形上的点 P (x, y)
P3(x, y + b)
P4(x, y - b)
归纳总结
向左平移 a 个单位对应点P2(x-a,y)
向右平移 a 个单位对应点 P1(x+a, y )
向上平移 b 个单位对应点 P3( x , y+b )
向下平移 b 个单位对应点 P4( x , y-b)
图形上的点 P(x,y)
随堂练习
4. 点 A1(6,3) 是由点A(-2,3)经过
得到的,点 B(4,3) 经过 得
到 B1(4,1).
1. 将点 A(3,2) 向上平移 2 个单位长度,得到 A1,则
A1 的坐标为 .
2. 将点 A(3,2) 向下平移 3 个单位长度,得到 A2,则
A2 的坐标为 .
3. 将点 A(3,2) 向左平移 4 个单位长度,得到 A3,则
A3 的坐标为 .
(3,4)
向右平移 8 个单位长度
向下平移 2 个单位长度
(3,-1)
(-1,2)
随堂练习
(x,y) (x,y+4) (x,y) (x-4,y)
(x,y) (x,y-2) (x,y) (x+2,y)
5.将坐标作如下变化时,图形将怎样变化?
向上平移 4 个单位长度
向左平移 4 个单位长度
向下平移 2 个单位长度
向右平移 2 个单位长度
随堂练习
6. 将点 P(m+1,n-2) 向上平移 3 个单位长度,得到点 Q(2,1-n),则点 A(m,n) 坐标为_________.
解:m+1=2,
n-2+3 =1-n,
故 m=1,n=0.
所以点 A 坐标为 (1,0).
(1,0)
随堂练习
7. 已知点 P(m-1,2m-1),点 Q(m2+m,m+1).
(1) 若点 Q 是由点 P 左右平移得到的,求出 m 的值,
并说明平移方向和距离;
(2) 点 Q 能否由点 P 上下平移得到?说明理由.
解:2m-1=m+1 ,
故m=2,
∴点 P 坐标为(1,3),
点 Q 坐标为(6,3).
∴点 Q 由点 P 向右平移 5 个单位长度得到的.
解:m-1=m2+m,
故 m2=-1,
∴点 Q 不能由点 P 上下平移得到.
课堂小结
图形在坐标系中的平移
沿x轴平移
沿y轴平移
纵坐标不变
横坐标加上一个正数,向右平移
横坐标减去一个正数,向左平移
横坐标不变
纵坐标加上一个正数,向上平移
纵坐标减去一个正数,向下平移
课后作业
完成教材习题3.3.
这节课你学到了什么?谈谈你的收获,
小结与反思
第3章 图形的平移和旋转
3.1 图形的平移
第2课时 坐标系中的点沿x轴、y轴
的一次平移
1.通过图形的平移,培养学生的探索能力
2.感受图形上点坐标变化与图形的平移变化之间的关系
1.图形上点坐标变化与图形平移之间的关系
2.直角坐标系中平移图形点坐标的变化情况
教学目标
重难点
温故知新
你还记得什么叫平移吗?
图形平移的性质是什么?
在平面内,把一个图形沿某个方向移动一定的距离,这种图形的变换叫做平移.
1. 新图形与原图形形状和大小不变,但位置改变;
2. 对应点的连线平行 (或在同一条直线上) 且相等.
探索新知 导入新课
0
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
-1
-2
-1
在直角坐标系中描出以下各点:
(0,0)(5,4)(3,0)(5,1)(5,1)(3,0)(4,-2)(0,0)
并用线段依次连接,看一看是什么图案.
探索新知
0
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
-1
-2
-1
图中的“鱼”是将坐标为: (0,0)(5,4)(3,0)(5,1)(5,-1)(3,0)(4,-2)(0,0)的点用线段依次连接而成的.
将这条“鱼”向右平移5个单位长度会怎样?
探索新知
0
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
-1
-2
-1
则坐标变化为:
(x,y) (0,0) (5,4) (3,0) (5,1) (5,-1) (3,0) (4,-2) (0,0)
(x+5,y) (5,0) (10,4) (8,0) (10,1) (10,-1) (8,0) (9,-2) (5,0)
原图形被向右平移5个单位
探索新知
0
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
-1
-2
-1
图中的“鱼”是将坐标为: (0,0)(5,4)(3,0)(5,1)(5,-1)(3,0)(4,-2)(0,0)的点用线段依次连接而成的.
将这条“鱼”向左平移2个单位长度会怎样?
探索新知
0
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
-1
-2
-1
则坐标变化为:
(x,y) (0,0) (5,4) (3,0) (5,1) (5,-1) (3,0) (4,-2) (0,0)
(x-2,y) (-2,0) (3,4) (1,0) (3,1) (3,-1) (1,0) (2,-2) (-2,0)
原图形被向左平移2个单位
归纳总结
原图形向左 (右) 平移 a (a>0) 个单位长度:
向右平移 a 个单位
原图形上的点 P (x, y)
向左平移 a 个单位
原图形上的点 P (x, y)
P1(x + a, y)
P2(x - a, y)
小牛试刀
1. 将点 A( -3 ,3 ) 向左平移 5 个单位长度,得到对应点坐标是
( -8,3 )
2.将点A(3,2)沿x轴向左平移4个单位长度得到点A′,与点A′关于y轴对称的点的坐标是( )
A.(-3,2) B.(-1,2)
C.(1,2) D.(1,-2)
C
探索新知
0
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
-1
-2
-1
图中的“鱼”是将坐标为: (0,0)(5,4)(3,0)(5,1)(5,-1)(3,0)(4,-2)(0,0)的点用线段依次连接而成的.
将这条“鱼”向上平移3个单位长度会怎样?
探索新知
0
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
-1
-2
-1
则坐标变化为:
(x,y) (0,0) (5,4) (3,0) (5,1) (5,-1) (3,0) (4,-2) (0,0)
(x,y+3) (0,3) (5,7) (3,3) (5,4) (5,2) (3,3) (4,1) (0,3)
原图形被向上平移3个单位
探索新知
将这条“鱼”向下平移2个单位长度会怎样?
0
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
-1
-2
-1
则坐标变化为:
(x,y) (0,0) (5,4) (3,0) (5,1) (5,-1) (3,0) (4,-2) (0,0)
(x,y-2) (0,-2) (5,2) (3,-2) (5,-1) (5,-3) (3,-2) (4,-4) (0,-2)
原图形被向下平移2个单位
总结新知
原图形向上 (下) 平移 b (b>0) 个单位长度:
向上平移 b 个单位
原图形上的点 P (x, y)
向下平移 b 个单位
原图形上的点 P (x, y)
P3(x, y + b)
P4(x, y - b)
归纳总结
向左平移 a 个单位对应点P2(x-a,y)
向右平移 a 个单位对应点 P1(x+a, y )
向上平移 b 个单位对应点 P3( x , y+b )
向下平移 b 个单位对应点 P4( x , y-b)
图形上的点 P(x,y)
随堂练习
4. 点 A1(6,3) 是由点A(-2,3)经过
得到的,点 B(4,3) 经过 得
到 B1(4,1).
1. 将点 A(3,2) 向上平移 2 个单位长度,得到 A1,则
A1 的坐标为 .
2. 将点 A(3,2) 向下平移 3 个单位长度,得到 A2,则
A2 的坐标为 .
3. 将点 A(3,2) 向左平移 4 个单位长度,得到 A3,则
A3 的坐标为 .
(3,4)
向右平移 8 个单位长度
向下平移 2 个单位长度
(3,-1)
(-1,2)
随堂练习
(x,y) (x,y+4) (x,y) (x-4,y)
(x,y) (x,y-2) (x,y) (x+2,y)
5.将坐标作如下变化时,图形将怎样变化?
向上平移 4 个单位长度
向左平移 4 个单位长度
向下平移 2 个单位长度
向右平移 2 个单位长度
随堂练习
6. 将点 P(m+1,n-2) 向上平移 3 个单位长度,得到点 Q(2,1-n),则点 A(m,n) 坐标为_________.
解:m+1=2,
n-2+3 =1-n,
故 m=1,n=0.
所以点 A 坐标为 (1,0).
(1,0)
随堂练习
7. 已知点 P(m-1,2m-1),点 Q(m2+m,m+1).
(1) 若点 Q 是由点 P 左右平移得到的,求出 m 的值,
并说明平移方向和距离;
(2) 点 Q 能否由点 P 上下平移得到?说明理由.
解:2m-1=m+1 ,
故m=2,
∴点 P 坐标为(1,3),
点 Q 坐标为(6,3).
∴点 Q 由点 P 向右平移 5 个单位长度得到的.
解:m-1=m2+m,
故 m2=-1,
∴点 Q 不能由点 P 上下平移得到.
课堂小结
图形在坐标系中的平移
沿x轴平移
沿y轴平移
纵坐标不变
横坐标加上一个正数,向右平移
横坐标减去一个正数,向左平移
横坐标不变
纵坐标加上一个正数,向上平移
纵坐标减去一个正数,向下平移
课后作业
完成教材习题3.3.
这节课你学到了什么?谈谈你的收获,
小结与反思
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
