沪教版三年级下册数学数学广场——数苹果(课件)(共17张PPT)
文档属性
| 名称 | 沪教版三年级下册数学数学广场——数苹果(课件)(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-26 00:00:00 | ||
图片预览

文档简介
(共17张PPT)
数学广场-数一数
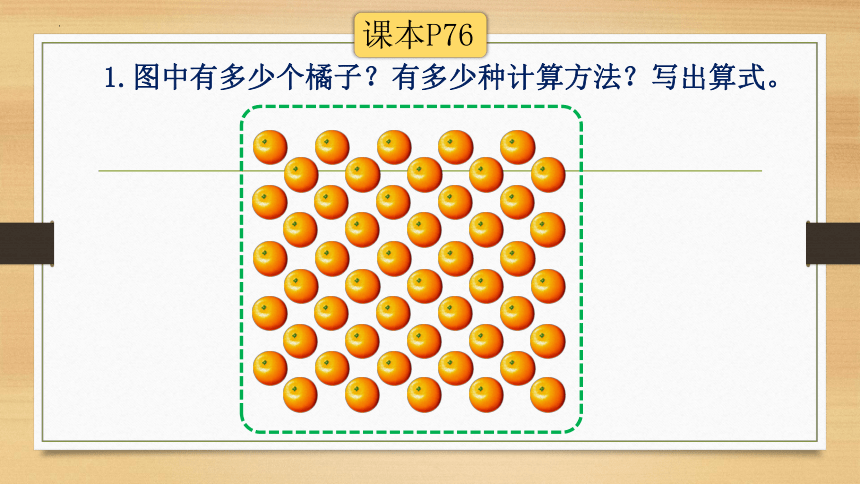
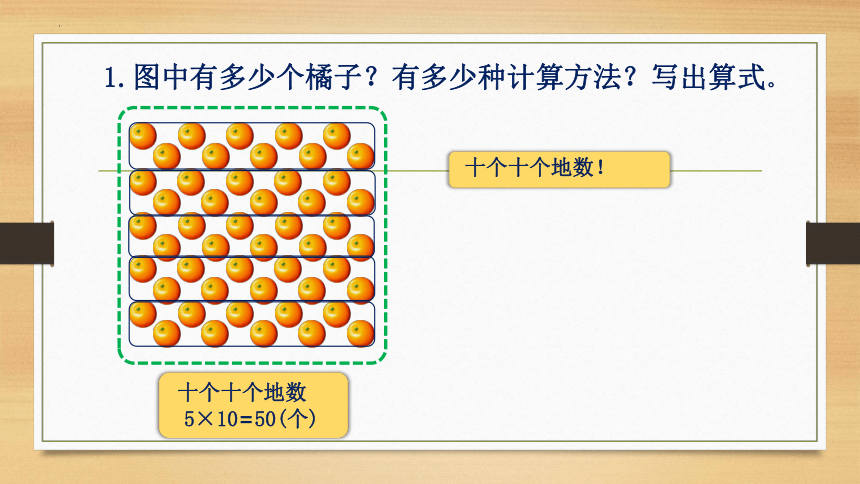
1.图中有多少个橘子?有多少种计算方法?写出算式。
课本P76
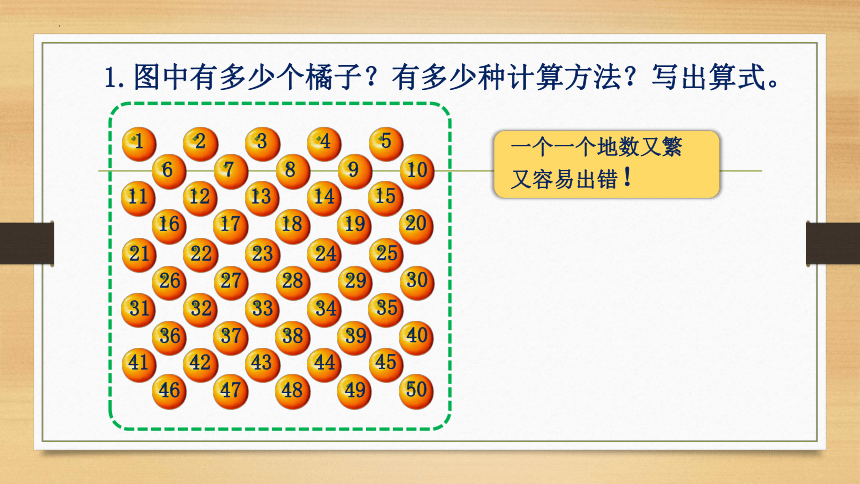
1.图中有多少个橘子?有多少种计算方法?写出算式。
一个一个地数又繁又容易出错!
1
2
3
4
5
11
12
13
14
15
21
22
23
24
25
16
17
18
19
20
6
7
8
9
10
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
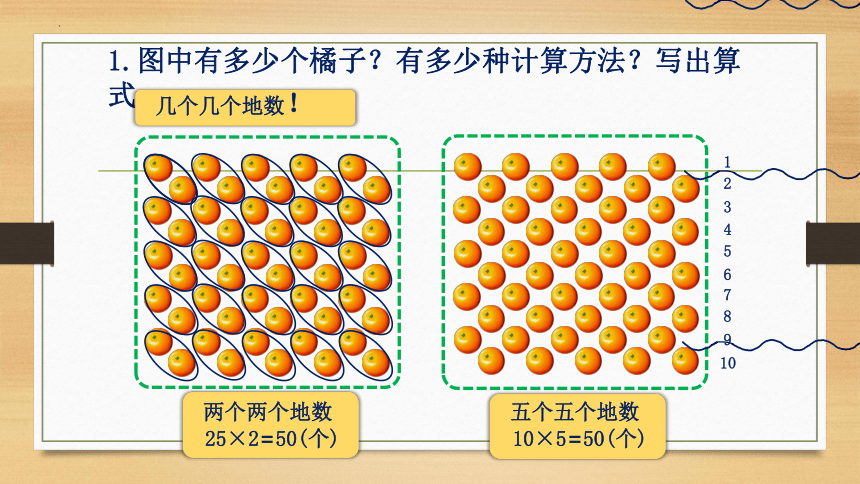
1.图中有多少个橘子?有多少种计算方法?写出算式。
几个几个地数!
两个两个地数
25×2=50(个)
五个五个地数
10×5=50(个)
1
2
3
4
5
6
7
8
9
10
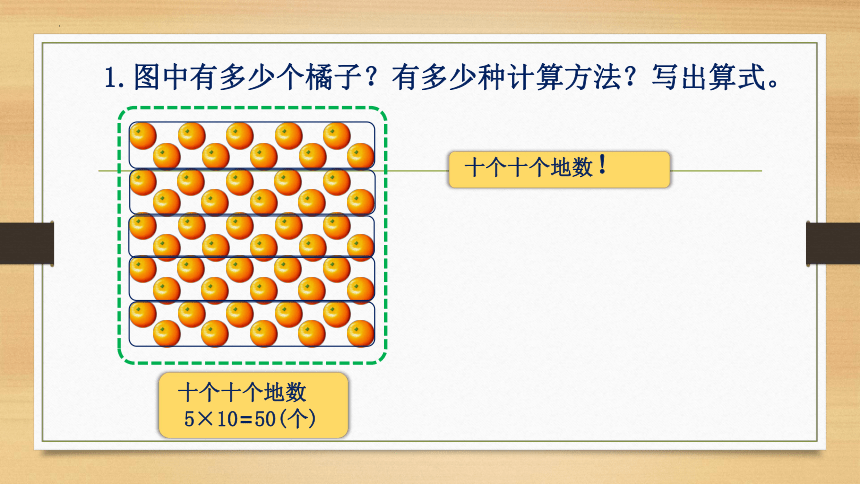
1.图中有多少个橘子?有多少种计算方法?写出算式。
十个十个地数!
十个十个地数
5×10=50(个)
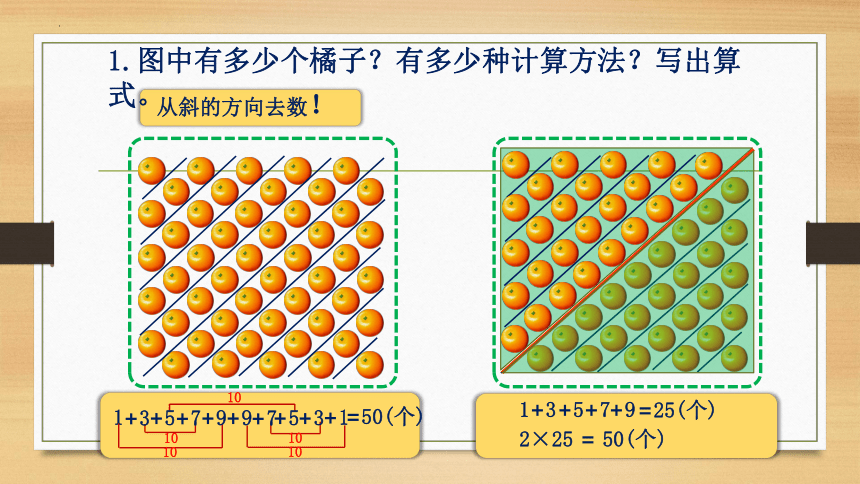
1.图中有多少个橘子?有多少种计算方法?写出算式。
十个十个地数!
十个十个地数
5×10=50(个)
从斜的方向去数!
1
1.图中有多少个橘子?有多少种计算方法?写出算式。
=25(个)
10
=50(个)
+3
+7
+5
+9
+9
+7
+5
+3
+1
2×25 = 50(个)
10
10
10
10
1
+3
+7
+5
+9
从斜的方向去数!
2
1.图中有多少个橘子?有多少种计算方法?写出算式。
2×20
10
=50(个)
+4
+8
+6
+10
+8
+6
+4
+2
10
=20(个)
10
10
10
2
+4
+8
+6
+10
=50(个)
1.图中有多少个橘子?有多少种计算方法?写出算式。
2.用边长为1cm的小正三角形排列并组合成一个大正三角形。
(1)有多少个边长都为1cm的正三角形?
(2)有多少个边长都为2cm的正三角形?
怎样才能一个不漏地把它们数出来?
1cm
课本P76
2.用边长为1cm的小正三角形排列并组合成一个大正三角形。
从上往下一层一层地数。
1
3
5
7
1+3+5+7=16(个)
答:有16个边长都为1cm的正三角形。
(1)有多少个边长都为1cm的正三角形?
2.用边长为1cm的小正三角形排列并组合成一个大正三角形。
我发现这里的小正三角形分向上(△)和向下(▽)。
△:1+2+3+4=10(个)
▽ :1+2+3=6(个)
10+6=16(个)
答:有16个边长都为1cm的正三角形。
(1)有多少个边长都为1cm的正三角形?
△
▽
1
1
2
3
4
2
3
2cm
怎样才能一个不漏地把它们数出来?
(2)有多少个边长都为2cm的正三角形?
2.用边长为1cm的小正三角形排列并组合成一个大正三角形。
课本P76
2.用边长为1cm的小正三角形排列并组合成一个大正三角形。
(2)有多少个边长都为2cm的正三角形?
从上往下一层一层地数。
1+2+3=6(个)
1
2
3
△:1+2+3=6(个)
▽:1个
6+1=7(个)
△
▽
1
1
2
3
答:有7个边长都为2cm的正三角形。
先分类,再计数。
答:有6个边长都为2cm的正三 角形。
×
√
2.用边长为1cm的小正三角形排列并组合成一个大正三角形。
3cm
☆有多少个边长都为3cm的正三角形?
△
▽
0
1
2
1+2=3(个)
答:有3个边长都为3cm的正三角形。
图中共有多少个正三角形?
2.用边长为1cm的小正三角形排列并组合成一个大正三角形。
☆
16
7
3
1
个数
边长1cm
边长2cm
正三角形
边长3cm
边长4cm
16+7+3+1=27(个)
答: 图中共有27个正三角形。
图中共有多少个正三角形?
一组一组计数。
先分类,再计数。
根据计数对象的特点,选择合适的计数方法。
有序地、全面地进行思考,能帮助我们在解决问题时不遗漏、不重复。
课堂小结
数学广场-数一数
1.图中有多少个橘子?有多少种计算方法?写出算式。
课本P76
1.图中有多少个橘子?有多少种计算方法?写出算式。
一个一个地数又繁又容易出错!
1
2
3
4
5
11
12
13
14
15
21
22
23
24
25
16
17
18
19
20
6
7
8
9
10
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
1.图中有多少个橘子?有多少种计算方法?写出算式。
几个几个地数!
两个两个地数
25×2=50(个)
五个五个地数
10×5=50(个)
1
2
3
4
5
6
7
8
9
10
1.图中有多少个橘子?有多少种计算方法?写出算式。
十个十个地数!
十个十个地数
5×10=50(个)
1.图中有多少个橘子?有多少种计算方法?写出算式。
十个十个地数!
十个十个地数
5×10=50(个)
从斜的方向去数!
1
1.图中有多少个橘子?有多少种计算方法?写出算式。
=25(个)
10
=50(个)
+3
+7
+5
+9
+9
+7
+5
+3
+1
2×25 = 50(个)
10
10
10
10
1
+3
+7
+5
+9
从斜的方向去数!
2
1.图中有多少个橘子?有多少种计算方法?写出算式。
2×20
10
=50(个)
+4
+8
+6
+10
+8
+6
+4
+2
10
=20(个)
10
10
10
2
+4
+8
+6
+10
=50(个)
1.图中有多少个橘子?有多少种计算方法?写出算式。
2.用边长为1cm的小正三角形排列并组合成一个大正三角形。
(1)有多少个边长都为1cm的正三角形?
(2)有多少个边长都为2cm的正三角形?
怎样才能一个不漏地把它们数出来?
1cm
课本P76
2.用边长为1cm的小正三角形排列并组合成一个大正三角形。
从上往下一层一层地数。
1
3
5
7
1+3+5+7=16(个)
答:有16个边长都为1cm的正三角形。
(1)有多少个边长都为1cm的正三角形?
2.用边长为1cm的小正三角形排列并组合成一个大正三角形。
我发现这里的小正三角形分向上(△)和向下(▽)。
△:1+2+3+4=10(个)
▽ :1+2+3=6(个)
10+6=16(个)
答:有16个边长都为1cm的正三角形。
(1)有多少个边长都为1cm的正三角形?
△
▽
1
1
2
3
4
2
3
2cm
怎样才能一个不漏地把它们数出来?
(2)有多少个边长都为2cm的正三角形?
2.用边长为1cm的小正三角形排列并组合成一个大正三角形。
课本P76
2.用边长为1cm的小正三角形排列并组合成一个大正三角形。
(2)有多少个边长都为2cm的正三角形?
从上往下一层一层地数。
1+2+3=6(个)
1
2
3
△:1+2+3=6(个)
▽:1个
6+1=7(个)
△
▽
1
1
2
3
答:有7个边长都为2cm的正三角形。
先分类,再计数。
答:有6个边长都为2cm的正三 角形。
×
√
2.用边长为1cm的小正三角形排列并组合成一个大正三角形。
3cm
☆有多少个边长都为3cm的正三角形?
△
▽
0
1
2
1+2=3(个)
答:有3个边长都为3cm的正三角形。
图中共有多少个正三角形?
2.用边长为1cm的小正三角形排列并组合成一个大正三角形。
☆
16
7
3
1
个数
边长1cm
边长2cm
正三角形
边长3cm
边长4cm
16+7+3+1=27(个)
答: 图中共有27个正三角形。
图中共有多少个正三角形?
一组一组计数。
先分类,再计数。
根据计数对象的特点,选择合适的计数方法。
有序地、全面地进行思考,能帮助我们在解决问题时不遗漏、不重复。
课堂小结
