数学人教A版(2019)选择性必修第二册4.4数学归纳法 课件(共27张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第二册4.4数学归纳法 课件(共27张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-27 10:14:13 | ||
图片预览







文档简介
(共27张PPT)
4.4 数学归纳法
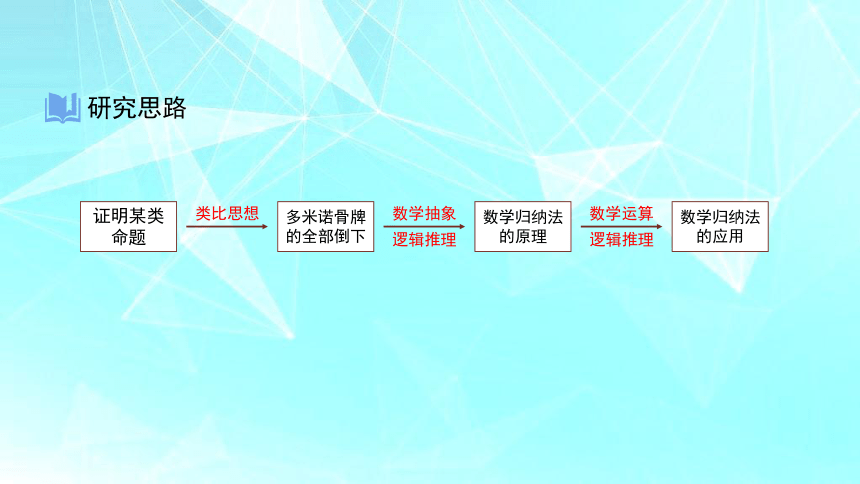
证明某类命题
多米诺骨牌的全部倒下
数学归纳法的原理
数学归纳法的应用
类比思想
数学抽象
逻辑推理
数学运算
研究思路
逻辑推理
等差数列{}的首项为,公差为d. 那么
,
……
归纳可得
如果{}是一个等差数列,怎样得到 ?
以上都是不完全归纳法的体现,其结果不一定正确。
如何解决不完全归纳法存在的问题呢?
问题1
问题导入
答案: , , .
问题2
已知数列 满足 , ,计算 ,
猜想其通项公式,并证明你的猜想.
猜想通项公式为:
(n∈N*)
(n∈N*)
已知数列 满足 , ,计算 ,
猜想其通项公式,并证明你的猜想.
问题2
答案:仅通过前几项不能得出所有的结果,这样得出的猜想不一定正确. 如:17世纪,法国大数学家费马发现,对于 ,分别验证n=1,2,3,4,这个数均为质数,从而猜测:对于任意的自然数,这个数都是质数.半个世纪后欧拉举出了反例:当n=5时,该数可拆成两个数的乘积.
追问1 仅通过前几项能得出所有的结果吗?这样得出的猜想一定正确吗?
猜想通项公式为:
(n∈N*)
(n∈N*)
问题2
已知数列 满足 , ,计算 ,
猜想其通项公式,并证明你的猜想.
答案:一般来说,与正整数n有关的命题,当n比较小时可以逐个验证. 但当n较大时,验证起来会很麻烦. 尤其是我们这里要证明n取所有正整数都成立,这是一个无限的问题,逐一验证是不可能的,我们无法用常规方法严格证明. 因此,我们很有必要寻求一种新的方法,这种方法能让我们通过有限个步骤的推理,证明n取所有正整数时命题都成立.
追问2 该如何证明这个猜想呢?
猜想通项公式为:
(n∈N*)
(n∈N*)
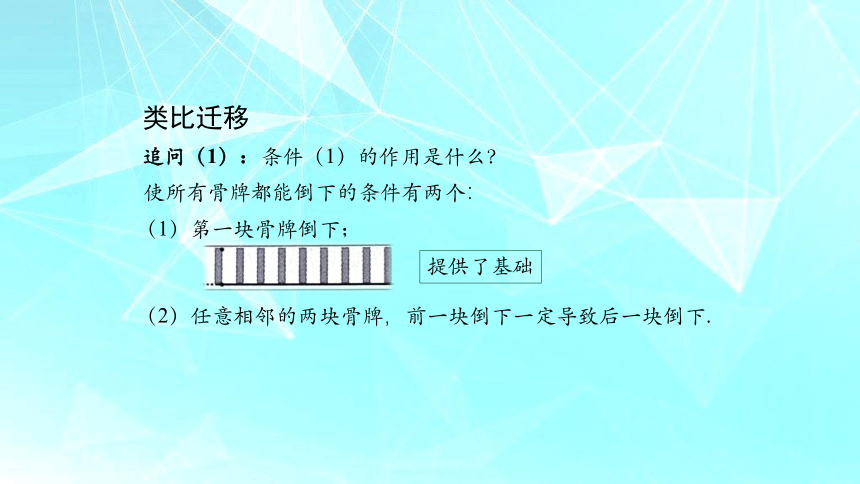
类比迁移
问题3 能使所有多米诺骨牌全部倒下的条件是什么?
问题3 能使所有多米诺骨牌全部倒下的条件是什么?
类比迁移
使所有骨牌都能倒下的条件有两个:
(1)第一块骨牌倒下;
(2)任意相邻的两块骨牌,前一块倒下一定导致后一块倒下.
追问(1):条件(1)的作用是什么?
类比迁移
使所有骨牌都能倒下的条件有两个:
(1)第一块骨牌倒下;
(2)任意相邻的两块骨牌,前一块倒下一定导致后一块倒下.
提供了基础
追问(2):条件(2)的作用是什么?
类比迁移
使所有骨牌都能倒下的条件有两个:
(1)第一块骨牌倒下;
(2)任意相邻的两块骨牌,前一块倒下一定导致后一块倒下.
提供了基础
递推关系:
第k块骨牌倒下
第k+1块骨牌倒下
由 及递推关系
追问(3):证明猜想“数列的通项公式是 ”与多米诺骨牌游戏有相似性吗?你能类比多米诺骨牌游戏解决这个问题吗?
类比迁移
由 及递推关系
……
递推关系:
命题:当n=k时猜想成立,则n=k+1时猜想也成立.
如果n=k时猜想成立,
那么
即当n=k+1时,猜想也成立.
,
即
骨牌原理 猜想的证明步骤
(1)第一块骨牌已经倒下 (1)证明n=1时,猜想正确
(2)证明“如果前一块倒下,则后一块也跟着倒下”这句话是真实的 (2)证明“当n=k时猜想成立,则n=k+1时猜想也成立”是真命题
根据(1)(2),所有骨牌都能倒下 根据(1)(2),这个猜想对一切正整数n都成立
一般地,证明一个与正整数n有关的命题,可按下列步骤进行:
问题4 什么是数学归纳法?
学习新知
追问(1):数学归纳法中的两个步骤都必要吗?
一般地,证明一个与正整数n有关的命题,可按下列步骤进行:
归纳奠基
归纳递推
追问(2):数学归纳法中的两个步骤之间有什么关系?
一般地,证明一个与正整数n有关的命题,可按下列步骤进行:
归纳奠基
归纳递推
追问(2):数学归纳法中的两个步骤之间有什么关系?
归纳奠基
归纳递推
记 是一个关于正整数n的命题.
追问(2):数学归纳法中的两个步骤之间有什么关系?
归纳奠基
归纳递推
为真;
记 是一个关于正整数n的命题.
追问(2):数学归纳法中的两个步骤之间有什么关系?
归纳奠基
归纳递推
为真;
记 是一个关于正整数n的命题.
,
追问(2):数学归纳法中的两个步骤之间有什么关系?
记 是一个关于正整数n的命题.
归纳奠基
归纳递推
为真;
真,
真
真,
真 .
……
……
条件:
,
追问(2):数学归纳法中的两个步骤之间有什么关系?
记 是一个关于正整数n的命题.
归纳奠基
归纳递推
为真;
条件:
结论:
为真.
,
追问(2):数学归纳法中的两个步骤之间有什么关系?
记 是一个关于正整数n的命题.
归纳奠基
归纳递推
为真;
条件:
结论:
为真.
例1 用数学归纳法证明:如果{an}是一个公差为d的等差数列,那么an=①对任何都成立.
在证明递推步骤时,必须使用归纳假设,并把“证明的目标”牢记在心.
证明:(1)当,左边,右边,①式成立.
(2)假设当时,①式成立,即
根据等差数列的定义,有
于是
即当时,①式也成立.
由(1)(2)可知,①式对任何都成立.
典例分析
证明:(1)当时, ①式的左边=12=1,
右边=×1×(1+1)×(2×1+1)==1,所以①式成立.
(2)假设当时, ①式成立,即
=
在上式两边同时加上,有
=
===
=即当, ①式也成立.
由(1)(2)可知, ①式对任何都成立.
例2 用数学归纳法证明: ①
例3 已知数列{an}满足试猜想数列{}的通项公式,并用数学归纳法加以证明.
同理可得
归纳上述结果,猜想an=(). ①
下面用数学归纳法证明这个猜想.
解:由2+1-+1=1,可得+1=().
由,可得==.
例3 已知数列{an}满足试猜想数列{}的通项公式,并用数学归纳法加以证明.
(1)当, ①式左边==0,右边==0,猜想成立.
(2)假设当时, ①式成立,即=,
那么====,
即当时,猜想也成立.
由(1)(2)可知,猜想对任何都成立.
例4设为正实数,为大于1的正整数,若数列的前项和为,试比较的大小,并用数学归纳法证明你的结论.
解法1:由已知可得
当,,可得;
当,,可得.
由此,我们猜想,当.
下面用数学归纳法证明这个猜想.
归纳奠基:证明当时命题成立;
归纳递推:以“当时命题成立”为条件,
推出“当时命题也成立”.
只要完成这两个步骤,就可以断定命题对从开始的所有正整数都成立,这种
证明方法称为数学归纳法.
课堂小结
4.4 数学归纳法
证明某类命题
多米诺骨牌的全部倒下
数学归纳法的原理
数学归纳法的应用
类比思想
数学抽象
逻辑推理
数学运算
研究思路
逻辑推理
等差数列{}的首项为,公差为d. 那么
,
……
归纳可得
如果{}是一个等差数列,怎样得到 ?
以上都是不完全归纳法的体现,其结果不一定正确。
如何解决不完全归纳法存在的问题呢?
问题1
问题导入
答案: , , .
问题2
已知数列 满足 , ,计算 ,
猜想其通项公式,并证明你的猜想.
猜想通项公式为:
(n∈N*)
(n∈N*)
已知数列 满足 , ,计算 ,
猜想其通项公式,并证明你的猜想.
问题2
答案:仅通过前几项不能得出所有的结果,这样得出的猜想不一定正确. 如:17世纪,法国大数学家费马发现,对于 ,分别验证n=1,2,3,4,这个数均为质数,从而猜测:对于任意的自然数,这个数都是质数.半个世纪后欧拉举出了反例:当n=5时,该数可拆成两个数的乘积.
追问1 仅通过前几项能得出所有的结果吗?这样得出的猜想一定正确吗?
猜想通项公式为:
(n∈N*)
(n∈N*)
问题2
已知数列 满足 , ,计算 ,
猜想其通项公式,并证明你的猜想.
答案:一般来说,与正整数n有关的命题,当n比较小时可以逐个验证. 但当n较大时,验证起来会很麻烦. 尤其是我们这里要证明n取所有正整数都成立,这是一个无限的问题,逐一验证是不可能的,我们无法用常规方法严格证明. 因此,我们很有必要寻求一种新的方法,这种方法能让我们通过有限个步骤的推理,证明n取所有正整数时命题都成立.
追问2 该如何证明这个猜想呢?
猜想通项公式为:
(n∈N*)
(n∈N*)
类比迁移
问题3 能使所有多米诺骨牌全部倒下的条件是什么?
问题3 能使所有多米诺骨牌全部倒下的条件是什么?
类比迁移
使所有骨牌都能倒下的条件有两个:
(1)第一块骨牌倒下;
(2)任意相邻的两块骨牌,前一块倒下一定导致后一块倒下.
追问(1):条件(1)的作用是什么?
类比迁移
使所有骨牌都能倒下的条件有两个:
(1)第一块骨牌倒下;
(2)任意相邻的两块骨牌,前一块倒下一定导致后一块倒下.
提供了基础
追问(2):条件(2)的作用是什么?
类比迁移
使所有骨牌都能倒下的条件有两个:
(1)第一块骨牌倒下;
(2)任意相邻的两块骨牌,前一块倒下一定导致后一块倒下.
提供了基础
递推关系:
第k块骨牌倒下
第k+1块骨牌倒下
由 及递推关系
追问(3):证明猜想“数列的通项公式是 ”与多米诺骨牌游戏有相似性吗?你能类比多米诺骨牌游戏解决这个问题吗?
类比迁移
由 及递推关系
……
递推关系:
命题:当n=k时猜想成立,则n=k+1时猜想也成立.
如果n=k时猜想成立,
那么
即当n=k+1时,猜想也成立.
,
即
骨牌原理 猜想的证明步骤
(1)第一块骨牌已经倒下 (1)证明n=1时,猜想正确
(2)证明“如果前一块倒下,则后一块也跟着倒下”这句话是真实的 (2)证明“当n=k时猜想成立,则n=k+1时猜想也成立”是真命题
根据(1)(2),所有骨牌都能倒下 根据(1)(2),这个猜想对一切正整数n都成立
一般地,证明一个与正整数n有关的命题,可按下列步骤进行:
问题4 什么是数学归纳法?
学习新知
追问(1):数学归纳法中的两个步骤都必要吗?
一般地,证明一个与正整数n有关的命题,可按下列步骤进行:
归纳奠基
归纳递推
追问(2):数学归纳法中的两个步骤之间有什么关系?
一般地,证明一个与正整数n有关的命题,可按下列步骤进行:
归纳奠基
归纳递推
追问(2):数学归纳法中的两个步骤之间有什么关系?
归纳奠基
归纳递推
记 是一个关于正整数n的命题.
追问(2):数学归纳法中的两个步骤之间有什么关系?
归纳奠基
归纳递推
为真;
记 是一个关于正整数n的命题.
追问(2):数学归纳法中的两个步骤之间有什么关系?
归纳奠基
归纳递推
为真;
记 是一个关于正整数n的命题.
,
追问(2):数学归纳法中的两个步骤之间有什么关系?
记 是一个关于正整数n的命题.
归纳奠基
归纳递推
为真;
真,
真
真,
真 .
……
……
条件:
,
追问(2):数学归纳法中的两个步骤之间有什么关系?
记 是一个关于正整数n的命题.
归纳奠基
归纳递推
为真;
条件:
结论:
为真.
,
追问(2):数学归纳法中的两个步骤之间有什么关系?
记 是一个关于正整数n的命题.
归纳奠基
归纳递推
为真;
条件:
结论:
为真.
例1 用数学归纳法证明:如果{an}是一个公差为d的等差数列,那么an=①对任何都成立.
在证明递推步骤时,必须使用归纳假设,并把“证明的目标”牢记在心.
证明:(1)当,左边,右边,①式成立.
(2)假设当时,①式成立,即
根据等差数列的定义,有
于是
即当时,①式也成立.
由(1)(2)可知,①式对任何都成立.
典例分析
证明:(1)当时, ①式的左边=12=1,
右边=×1×(1+1)×(2×1+1)==1,所以①式成立.
(2)假设当时, ①式成立,即
=
在上式两边同时加上,有
=
===
=即当, ①式也成立.
由(1)(2)可知, ①式对任何都成立.
例2 用数学归纳法证明: ①
例3 已知数列{an}满足试猜想数列{}的通项公式,并用数学归纳法加以证明.
同理可得
归纳上述结果,猜想an=(). ①
下面用数学归纳法证明这个猜想.
解:由2+1-+1=1,可得+1=().
由,可得==.
例3 已知数列{an}满足试猜想数列{}的通项公式,并用数学归纳法加以证明.
(1)当, ①式左边==0,右边==0,猜想成立.
(2)假设当时, ①式成立,即=,
那么====,
即当时,猜想也成立.
由(1)(2)可知,猜想对任何都成立.
例4设为正实数,为大于1的正整数,若数列的前项和为,试比较的大小,并用数学归纳法证明你的结论.
解法1:由已知可得
当,,可得;
当,,可得.
由此,我们猜想,当.
下面用数学归纳法证明这个猜想.
归纳奠基:证明当时命题成立;
归纳递推:以“当时命题成立”为条件,
推出“当时命题也成立”.
只要完成这两个步骤,就可以断定命题对从开始的所有正整数都成立,这种
证明方法称为数学归纳法.
课堂小结
