5.5.2 简单的三角恒等变换(1) 课件(共21张PPT)
文档属性
| 名称 | 5.5.2 简单的三角恒等变换(1) 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-27 00:00:00 | ||
图片预览








文档简介
(共21张PPT)
第5章 三角函数
5.5.2 简单的三角恒等变换(1)
人教A版(2019)
教学目标
学习目标 数学素养
1.能用二倍角公式的变形公式推导出半角的正弦、余弦、正切公式; 1.数学推理素养.
2.能利用三角公式进行求值、化简、恒等式证明. 2.逻辑推理素养、数学运算素养.
温故知新
两角和(差)正弦、余弦、正切公式
(S(α+β))
(S(α-β))
(C(α+β))
(C(α-β))
(T(α-β))
(T(α+β))
温故知新
倍角公式
公式变形:
升幂降角公式
升角降幂公式
新知形成
解:
【例1】试以表示.
是的二倍角.在倍角公式中,以代替,以代替,得
.
∴. ②
∴. ①
.
.
观察与,逆发现它们之间有什么关系?联想前面学过的公式,你有思路吗?
在倍角公式中,以代替,以代替,得
将①②两式左右两边相除,得
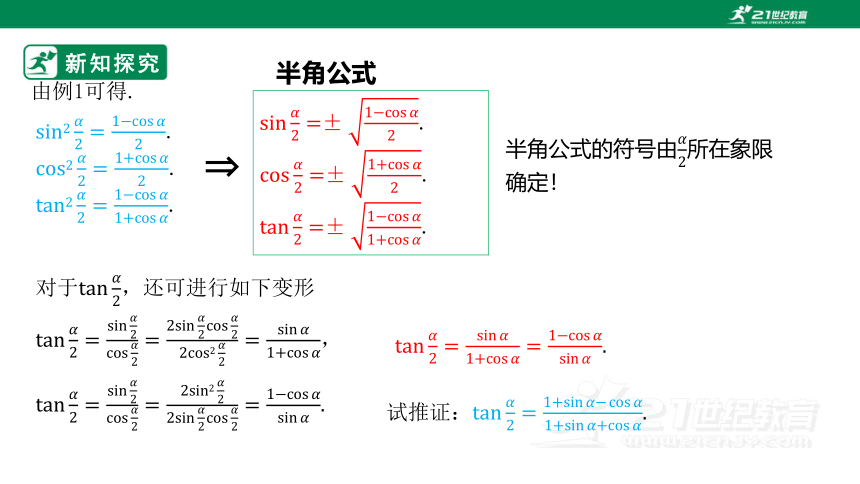
新知探究
由例1可得.
.
.
.
对于,还可进行如下变形
,
.
.
.
半角公式
.
.
试推证:.
半角公式的符号由所在象限确定!
新知形成
解:
【例2】 ⑴设,则=( )
A.- B. C. D.
⑵已知,化简:.
⑴∵, ∴.
∴,故选D.
又.
D
新知形成
解:
【例2】 ⑴设,则=( )
A.- B. C. D.
⑵已知,化简:.
.
⑵∵, ∴,即.
原式.
.
新知形成
1.化简问题中的“三变”技巧
(1)变角:三角变换时通常先寻找式子中各角之间的联系,通过拆、凑等手段消除角之间的差异,合理选择联系它们的公式.
(2)变名:观察三角函数种类的差异,尽量统一函数的名称,如统一为弦或统一为切.
(3)变式:观察式子的结构形式的差异,选择适当的变形途径,如升幂、降幂、配方、开方等.
2.利用半角公式求值的思路
(1)看角:看已知角与待求角的2倍关系.
(2)明范围:求出相应半角的范围为定符号作准备.
(3)选公式:涉及半角公式的正切值时,常用,涉及半角公式的正、余弦值时,常利用,计算.
初试身手
2.已知,且,试求和的值.
3.已知等腰三角形的顶角的余弦等于,求这个三角形的一个底角的正切.
解:
2.∵,∴,
∴.
.
P226练习
初试身手
2.已知,且,试求和的值.
3.已知等腰三角形的顶角的余弦等于,求这个三角形的一个底角的正切.
解:
.
3.设此三角形的顶角为,底角为,
则.
∴
.
P226练习
.
则此三角形的一个底角的正切为.
新知探求
【例3】求证:
⑴ ;
⑵ .
证明:
⑴∵
比较一下(2)式和(1)的结构,由此你能想到用什么方法
.
,可设,换元就可由⑴式得到⑵式.
.
∴.
将以上两式的左右两边分别相加,得
新知探求
【例3】求证:
⑴ ;
⑵ .
证明:
⑵由⑴可得
①
把代入①,即得
.
设,则.
如果不用(1)的结果,(2)式又如何证明
新知探求
【例3】求证:
⑴ ;
⑵ .
另证:
⑵
.
.
.
.
.
则.
初试身手
4.求证:
⑴ ;
⑵;
⑶ .
证明:
解得 .
即.
∴.
⑴令,
P226练习
⑵,
∴.
.
即.
⑶由⑵联立的方程组解得
即.
解得.
初试身手
5.求证:
⑴; ⑵;
证明:
①-②,得 .
.
. ②
⑴, ①
P226练习
⑵, ③
. ④
.
③+④,得
课堂小结
1.半角得正弦、余弦、正切公式的推导
2.注意:
学习三角恒等变换,千万不要只顾死记硬背公式,而忽视对思想方法的理解,要学会借助前面几个有限的公式来推导后继公式,立足于在公式推导过程中记忆公式和运用公式.
.
.
.
.
.
.
半角公式的符号由所在象限确定!
作业布置
作业:P229 习题5.5 第9,10题.
补充:
1.已知,求的值.
2.已知,且,求的值.
尽情享受学习数学的快乐吧!
我们下节课再见!
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
第5章 三角函数
5.5.2 简单的三角恒等变换(1)
人教A版(2019)
教学目标
学习目标 数学素养
1.能用二倍角公式的变形公式推导出半角的正弦、余弦、正切公式; 1.数学推理素养.
2.能利用三角公式进行求值、化简、恒等式证明. 2.逻辑推理素养、数学运算素养.
温故知新
两角和(差)正弦、余弦、正切公式
(S(α+β))
(S(α-β))
(C(α+β))
(C(α-β))
(T(α-β))
(T(α+β))
温故知新
倍角公式
公式变形:
升幂降角公式
升角降幂公式
新知形成
解:
【例1】试以表示.
是的二倍角.在倍角公式中,以代替,以代替,得
.
∴. ②
∴. ①
.
.
观察与,逆发现它们之间有什么关系?联想前面学过的公式,你有思路吗?
在倍角公式中,以代替,以代替,得
将①②两式左右两边相除,得
新知探究
由例1可得.
.
.
.
对于,还可进行如下变形
,
.
.
.
半角公式
.
.
试推证:.
半角公式的符号由所在象限确定!
新知形成
解:
【例2】 ⑴设,则=( )
A.- B. C. D.
⑵已知,化简:.
⑴∵, ∴.
∴,故选D.
又.
D
新知形成
解:
【例2】 ⑴设,则=( )
A.- B. C. D.
⑵已知,化简:.
.
⑵∵, ∴,即.
原式.
.
新知形成
1.化简问题中的“三变”技巧
(1)变角:三角变换时通常先寻找式子中各角之间的联系,通过拆、凑等手段消除角之间的差异,合理选择联系它们的公式.
(2)变名:观察三角函数种类的差异,尽量统一函数的名称,如统一为弦或统一为切.
(3)变式:观察式子的结构形式的差异,选择适当的变形途径,如升幂、降幂、配方、开方等.
2.利用半角公式求值的思路
(1)看角:看已知角与待求角的2倍关系.
(2)明范围:求出相应半角的范围为定符号作准备.
(3)选公式:涉及半角公式的正切值时,常用,涉及半角公式的正、余弦值时,常利用,计算.
初试身手
2.已知,且,试求和的值.
3.已知等腰三角形的顶角的余弦等于,求这个三角形的一个底角的正切.
解:
2.∵,∴,
∴.
.
P226练习
初试身手
2.已知,且,试求和的值.
3.已知等腰三角形的顶角的余弦等于,求这个三角形的一个底角的正切.
解:
.
3.设此三角形的顶角为,底角为,
则.
∴
.
P226练习
.
则此三角形的一个底角的正切为.
新知探求
【例3】求证:
⑴ ;
⑵ .
证明:
⑴∵
比较一下(2)式和(1)的结构,由此你能想到用什么方法
.
,可设,换元就可由⑴式得到⑵式.
.
∴.
将以上两式的左右两边分别相加,得
新知探求
【例3】求证:
⑴ ;
⑵ .
证明:
⑵由⑴可得
①
把代入①,即得
.
设,则.
如果不用(1)的结果,(2)式又如何证明
新知探求
【例3】求证:
⑴ ;
⑵ .
另证:
⑵
.
.
.
.
.
则.
初试身手
4.求证:
⑴ ;
⑵;
⑶ .
证明:
解得 .
即.
∴.
⑴令,
P226练习
⑵,
∴.
.
即.
⑶由⑵联立的方程组解得
即.
解得.
初试身手
5.求证:
⑴; ⑵;
证明:
①-②,得 .
.
. ②
⑴, ①
P226练习
⑵, ③
. ④
.
③+④,得
课堂小结
1.半角得正弦、余弦、正切公式的推导
2.注意:
学习三角恒等变换,千万不要只顾死记硬背公式,而忽视对思想方法的理解,要学会借助前面几个有限的公式来推导后继公式,立足于在公式推导过程中记忆公式和运用公式.
.
.
.
.
.
.
半角公式的符号由所在象限确定!
作业布置
作业:P229 习题5.5 第9,10题.
补充:
1.已知,求的值.
2.已知,且,求的值.
尽情享受学习数学的快乐吧!
我们下节课再见!
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
