四川省达州市大竹县文星中学2014-2015学年八年级下学期期中考试数学试题
文档属性
| 名称 | 四川省达州市大竹县文星中学2014-2015学年八年级下学期期中考试数学试题 |  | |
| 格式 | zip | ||
| 文件大小 | 189.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-05-22 10:41:35 | ||
图片预览


文档简介
四川省大竹县文星中学2015年春初二下期期中检测
数学试卷
(满分100分,时间90分钟)
第I卷(选择题)
选择题:每小题3分,共30分。
1. 已知等腰三角形一边长为4,另一边长为8,则这个等腰三角形的周长为( )
A.16 B.20或16 C.20 D.12
2. 如图所示,在Rt△ABC中,∠C=90°,∠A=30°,BD是∠ABC的平分线,CD=5 cm,则AB的长为( )
A.5 cm B. cm C.10 cm D. cm
( http: / / www.21cnjy.com )
3. 如图,直线l∥m∥n,等边△ABC的顶点B、C分别在直线n和m上,边BC与直线n所夹锐角为25°,则∠α的度数为( )
A.25° B.45° C.35° D.30°
( http: / / www.21cnjy.com )
4. 若不等式组有实数解,则实数m的取值范围是( )
A.m≤ B.m< C.m> D.m≥
5. a,b都是实数,且a<b,则下列不等式的变形正确的是( )
A.a+x>b+x B.-a+1<-b+1
C.3a<3b D.>
6. 已知x2-2=y,则x(x-3y)+y(3x-1)-2的值是( )
A.-2 B.0 C.2 D.4
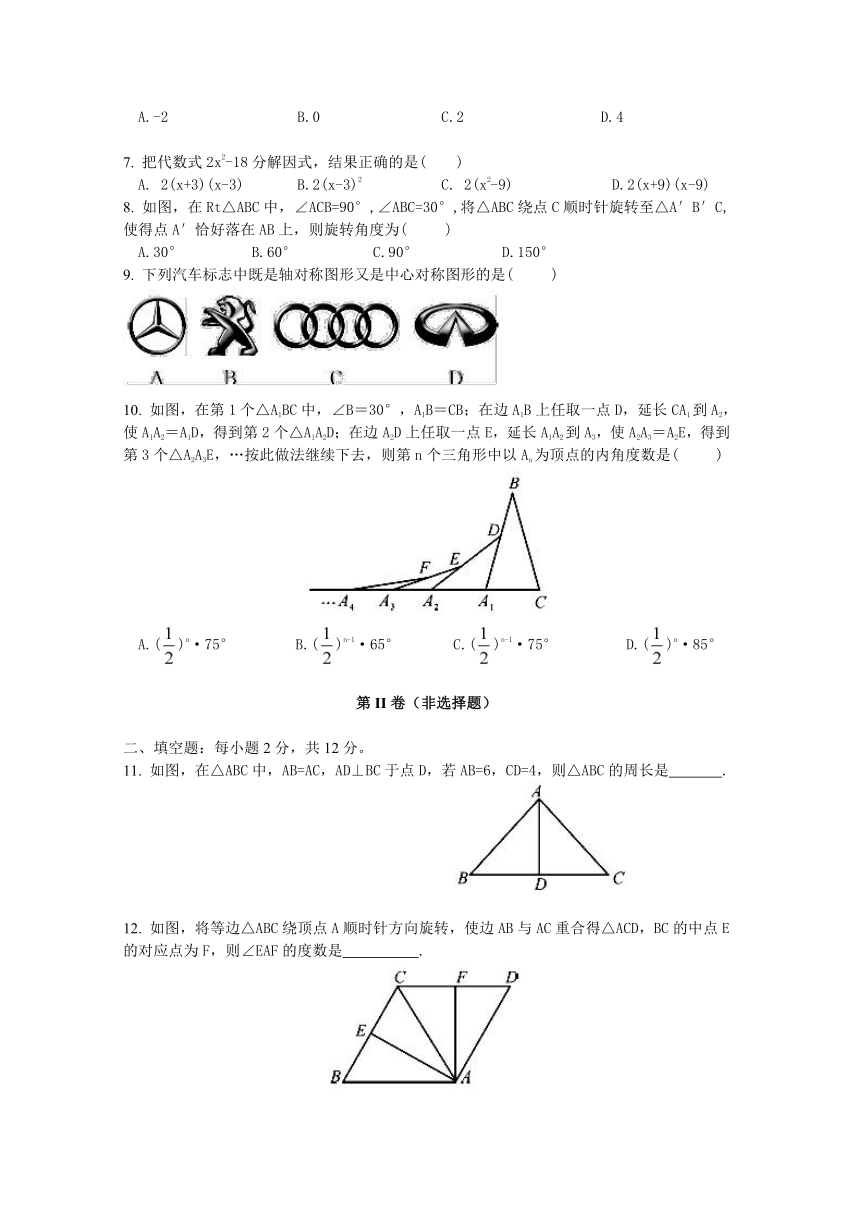
7. 把代数式2x2-18分解因式,结果正确的是( )
A. 2(x+3)(x-3) B.2(x-3)2 C. 2(x2-9) D.2(x+9)(x-9)
8. 如图,在Rt△ABC中,∠ACB=9 ( http: / / www.21cnjy.com )0°,∠ABC=30°,将△ABC绕点C顺时针旋转至△A′B′C,使得点A′恰好落在AB上,则旋转角度为( )
A.30° B.60° C.90° D.150°
9. 下列汽车标志中既是轴对称图形又是中心对称图形的是( )
( http: / / www.21cnjy.com )
10. 如图,在第1个△A ( http: / / www.21cnjy.com )1BC中,∠B=30°,A1B=CB;在边A1B上任取一点D,延长CA1到A2,使A1A2=A1D,得到第2个△A1A2D;在边A2D上任取一点E,延长A1A2到A3,使A2A3=A2E,得到第3个△A2A3E,…按此做法继续下去,则第n个三角形中以An为顶点的内角度数是( )
( http: / / www.21cnjy.com )
A.()n·75° B.()n-1·65° C.()n-1·75° D.()n·85°
第II卷(非选择题)
二、填空题:每小题2分,共12分。
11. 如图,在△ABC中,AB=AC,AD⊥BC于点D,若AB=6,CD=4,则△ABC的周长是 .
( http: / / www.21cnjy.com )
12. 如图,将等边△ABC绕顶点A顺 ( http: / / www.21cnjy.com )时针方向旋转,使边AB与AC重合得△ACD,BC的中点E的对应点为F,则∠EAF的度数是 .
( http: / / www.21cnjy.com )
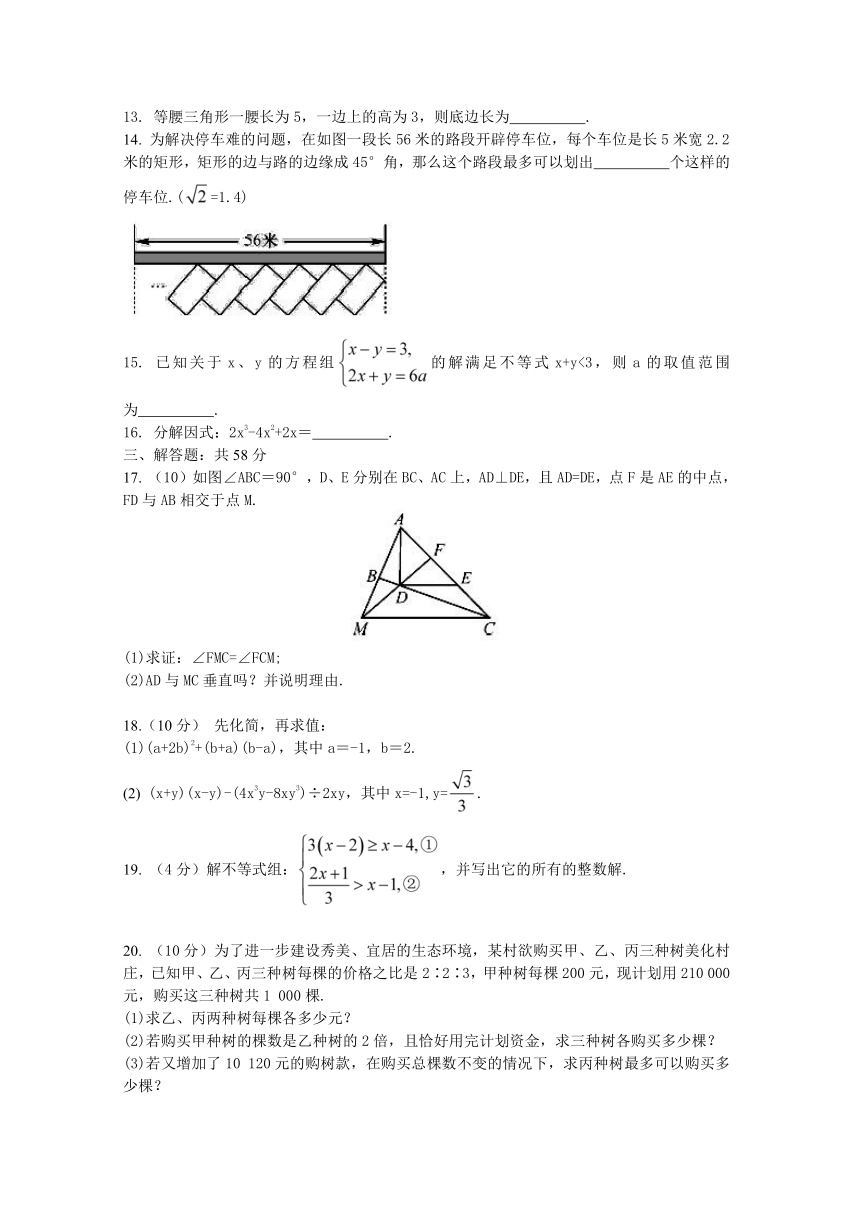
13. 等腰三角形一腰长为5,一边上的高为3,则底边长为 .
14. 为解决停车难的问题,在如图一段长56米的路段开辟停车位,每个车位是长5米宽2.2米的矩形,矩形的边与路的边缘成45°角,那么这个路段最多可以划出 个这样的停车位.(=1.4)
( http: / / www.21cnjy.com )
15. 已知关于x、y的方程组的解满足不等式x+y<3,则a的取值范围为 .
16. 分解因式:2x3-4x2+2x= .
三、解答题:共58分
17. (10)如图∠ABC=90°,D、E分别在BC、AC上,AD⊥DE,且AD=DE,点F是AE的中点,FD与AB相交于点M.
( http: / / www.21cnjy.com )
(1)求证:∠FMC=∠FCM;
(2)AD与MC垂直吗?并说明理由.
18.(10分) 先化简,再求值:
(1)(a+2b)2+(b+a)(b-a),其中a=-1,b=2.
(2) (x+y)(x-y)-(4x3y-8xy3)÷2xy,其中x=-1,y=.
19. (4分)解不等式组: ( http: / / www.21cnjy.com ),并写出它的所有的整数解.
20. (10分)为了进一步建设秀 ( http: / / www.21cnjy.com )美、宜居的生态环境,某村欲购买甲、乙、丙三种树美化村庄,已知甲、乙、丙三种树每棵的价格之比是2∶2∶3,甲种树每棵200元,现计划用210 000元,购买这三种树共1 000棵.
(1)求乙、丙两种树每棵各多少元?
(2)若购买甲种树的棵数是乙种树的2倍,且恰好用完计划资金,求三种树各购买多少棵?
(3)若又增加了10 120元的购树款,在购买总棵数不变的情况下,求丙种树最多可以购买多少棵?
21.(14分)在Rt△ABC中, ( http: / / www.21cnjy.com )∠A=90°,有一个锐角为60°,BC=6.若P在直线AC上(不与点A,C重合),且∠ABP=30°,求CP的长.
22. (14分)如图1,在△ABC中,AE⊥BC于E,AE=BE,D是AE上的一点,且DE=CE,连接BD、AC.
(1)试判断BD与AC的位置关系和数量关系,并说明理由.
(2)如图2,若将△DCE绕点E旋转一定的角度后,试判断BD与AC的位置关系和数量关系是否发生变化,并说明理由.
(3)如图3,若将(2)中的等腰直角三角形都换成等边三角形,其他条件不变,
①试猜想BD与AC的数量关系,并说明理由.
②你能求出BD与AC的夹角度数吗?如果能,请直接写出夹角度数;如果不能,请说明理由.
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
四川省大竹县文星中学2015年春初二下期期中检测数学参考答案
1-5.CDCDC 6-10. BACBC
11. 20
12. 60°
13. 8或或
14.17
15. a<1
16. 2x(x-1)2
17. (1)证明:∵△ADE是等腰直角三角形,F是AE的中点,
∴DF⊥AE,DF=AF=EF.
又∵∠ABC=90°,∠DCF,∠AMF都与∠MAC互余,
∴∠DCF=∠AMF.
又∵∠DFC=∠AFM=90°,∴△DFC≌△AFM.
∴CF=MF,∴∠FMC=∠FCM.
(2)AD⊥MC.理由如下:
由(1)知∠MFC=90°,FD=FE,FM=FC,
∴∠FDE=∠FMC=45°,
∴DE∥CM,∴AD⊥MC.
18.解:(1) 原式=a2+4ab+4b2+b2-a2=4ab+5b2.
当a=-1,b=2时,原式=4×(-1)×2+5×22=12.
(2)原式=x2-y2-2x2+4y2=-x2+3y2.
当x=-1,y=时,原式=-(-1)2+3×()2=0
19. 解:由①得x≥1.
由②得x<4.
∴原不等式组的解集是1≤x<4,
∴原不等式组的所有的整数解是1、2、3.
20.解:(1)∵甲、乙、丙三种树每棵的价格之比是2∶2∶3,甲种树每棵200元,
∴乙种树每棵的价格200元,
丙种树每棵的价格200×=300(元).
(2)设购买乙种树x棵,则购买甲种树2x棵,购买丙种树(1 000-3x)棵,依题意得
200×2x+200×x+300(1 000-3x)=210 000.
解得x=300.
∴购买甲种树600棵,购买乙种树300棵,购买丙种树100棵.
(3)设若购买丙种树y棵,则购买甲、乙两种树共(1 000-y)棵,依题意得
200(1 000-y)+300y≤210 000+10 120.
解得y≤201.2.
∵y为正整数,
∴y=201.
∴丙种树最多可以购买201棵.
21.
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
22. (1)BD与AC的位置关系是:BD⊥AC,数量关系是BD=AC.理由如下:
如图1,延长BD交AC于点F.
( http: / / www.21cnjy.com )
∵AE⊥BC于E,∴∠BED=∠AEC=90°.
又∵AE=BE,DE=CE,∴△DBE≌△CAE,
∴BD=AC,∠DBE=∠CAE,∠BDE=∠ACE.
∵∠BDE=∠ADF,∴∠ADF=∠ACE.
∵∠ACE+∠CAE=90°,∴∠ADF+∠CAE=90°,
∴BD⊥AC.
(2)如图2,∵∠AEB=∠DEC=90°,
∴∠AEB+∠AED=∠DEC+∠AED,
即∠BED=∠AEC.
∵AE=BE,DE=CE,∴△BED≌△AEC,
∴BD=AC,∠BDE=∠ACE,∠DBE=∠CAE.
∵∠BFC=∠ACD+∠CDE+∠BDE=∠ACD+∠CDE+∠ACE=90°,
∴BD⊥AC.
(3)①BD与AC的数量关系是:BD=AC.
∵△ABE和△DCE是等边三角形,
∴∠AEB=∠ABE=60°,AE=BE,
∠DEC=∠DCE=60°,DE=CE,
∴∠AEB+∠AED=∠DEC+∠AED,
即∠BED=∠AEC,
∴△BED≌△AEC.
∴BD=AC.
②BD与AC的夹角度数为60°或120°.
数学试卷
(满分100分,时间90分钟)
第I卷(选择题)
选择题:每小题3分,共30分。
1. 已知等腰三角形一边长为4,另一边长为8,则这个等腰三角形的周长为( )
A.16 B.20或16 C.20 D.12
2. 如图所示,在Rt△ABC中,∠C=90°,∠A=30°,BD是∠ABC的平分线,CD=5 cm,则AB的长为( )
A.5 cm B. cm C.10 cm D. cm
( http: / / www.21cnjy.com )
3. 如图,直线l∥m∥n,等边△ABC的顶点B、C分别在直线n和m上,边BC与直线n所夹锐角为25°,则∠α的度数为( )
A.25° B.45° C.35° D.30°
( http: / / www.21cnjy.com )
4. 若不等式组有实数解,则实数m的取值范围是( )
A.m≤ B.m< C.m> D.m≥
5. a,b都是实数,且a<b,则下列不等式的变形正确的是( )
A.a+x>b+x B.-a+1<-b+1
C.3a<3b D.>
6. 已知x2-2=y,则x(x-3y)+y(3x-1)-2的值是( )
A.-2 B.0 C.2 D.4
7. 把代数式2x2-18分解因式,结果正确的是( )
A. 2(x+3)(x-3) B.2(x-3)2 C. 2(x2-9) D.2(x+9)(x-9)
8. 如图,在Rt△ABC中,∠ACB=9 ( http: / / www.21cnjy.com )0°,∠ABC=30°,将△ABC绕点C顺时针旋转至△A′B′C,使得点A′恰好落在AB上,则旋转角度为( )
A.30° B.60° C.90° D.150°
9. 下列汽车标志中既是轴对称图形又是中心对称图形的是( )
( http: / / www.21cnjy.com )
10. 如图,在第1个△A ( http: / / www.21cnjy.com )1BC中,∠B=30°,A1B=CB;在边A1B上任取一点D,延长CA1到A2,使A1A2=A1D,得到第2个△A1A2D;在边A2D上任取一点E,延长A1A2到A3,使A2A3=A2E,得到第3个△A2A3E,…按此做法继续下去,则第n个三角形中以An为顶点的内角度数是( )
( http: / / www.21cnjy.com )
A.()n·75° B.()n-1·65° C.()n-1·75° D.()n·85°
第II卷(非选择题)
二、填空题:每小题2分,共12分。
11. 如图,在△ABC中,AB=AC,AD⊥BC于点D,若AB=6,CD=4,则△ABC的周长是 .
( http: / / www.21cnjy.com )
12. 如图,将等边△ABC绕顶点A顺 ( http: / / www.21cnjy.com )时针方向旋转,使边AB与AC重合得△ACD,BC的中点E的对应点为F,则∠EAF的度数是 .
( http: / / www.21cnjy.com )
13. 等腰三角形一腰长为5,一边上的高为3,则底边长为 .
14. 为解决停车难的问题,在如图一段长56米的路段开辟停车位,每个车位是长5米宽2.2米的矩形,矩形的边与路的边缘成45°角,那么这个路段最多可以划出 个这样的停车位.(=1.4)
( http: / / www.21cnjy.com )
15. 已知关于x、y的方程组的解满足不等式x+y<3,则a的取值范围为 .
16. 分解因式:2x3-4x2+2x= .
三、解答题:共58分
17. (10)如图∠ABC=90°,D、E分别在BC、AC上,AD⊥DE,且AD=DE,点F是AE的中点,FD与AB相交于点M.
( http: / / www.21cnjy.com )
(1)求证:∠FMC=∠FCM;
(2)AD与MC垂直吗?并说明理由.
18.(10分) 先化简,再求值:
(1)(a+2b)2+(b+a)(b-a),其中a=-1,b=2.
(2) (x+y)(x-y)-(4x3y-8xy3)÷2xy,其中x=-1,y=.
19. (4分)解不等式组: ( http: / / www.21cnjy.com ),并写出它的所有的整数解.
20. (10分)为了进一步建设秀 ( http: / / www.21cnjy.com )美、宜居的生态环境,某村欲购买甲、乙、丙三种树美化村庄,已知甲、乙、丙三种树每棵的价格之比是2∶2∶3,甲种树每棵200元,现计划用210 000元,购买这三种树共1 000棵.
(1)求乙、丙两种树每棵各多少元?
(2)若购买甲种树的棵数是乙种树的2倍,且恰好用完计划资金,求三种树各购买多少棵?
(3)若又增加了10 120元的购树款,在购买总棵数不变的情况下,求丙种树最多可以购买多少棵?
21.(14分)在Rt△ABC中, ( http: / / www.21cnjy.com )∠A=90°,有一个锐角为60°,BC=6.若P在直线AC上(不与点A,C重合),且∠ABP=30°,求CP的长.
22. (14分)如图1,在△ABC中,AE⊥BC于E,AE=BE,D是AE上的一点,且DE=CE,连接BD、AC.
(1)试判断BD与AC的位置关系和数量关系,并说明理由.
(2)如图2,若将△DCE绕点E旋转一定的角度后,试判断BD与AC的位置关系和数量关系是否发生变化,并说明理由.
(3)如图3,若将(2)中的等腰直角三角形都换成等边三角形,其他条件不变,
①试猜想BD与AC的数量关系,并说明理由.
②你能求出BD与AC的夹角度数吗?如果能,请直接写出夹角度数;如果不能,请说明理由.
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
四川省大竹县文星中学2015年春初二下期期中检测数学参考答案
1-5.CDCDC 6-10. BACBC
11. 20
12. 60°
13. 8或或
14.17
15. a<1
16. 2x(x-1)2
17. (1)证明:∵△ADE是等腰直角三角形,F是AE的中点,
∴DF⊥AE,DF=AF=EF.
又∵∠ABC=90°,∠DCF,∠AMF都与∠MAC互余,
∴∠DCF=∠AMF.
又∵∠DFC=∠AFM=90°,∴△DFC≌△AFM.
∴CF=MF,∴∠FMC=∠FCM.
(2)AD⊥MC.理由如下:
由(1)知∠MFC=90°,FD=FE,FM=FC,
∴∠FDE=∠FMC=45°,
∴DE∥CM,∴AD⊥MC.
18.解:(1) 原式=a2+4ab+4b2+b2-a2=4ab+5b2.
当a=-1,b=2时,原式=4×(-1)×2+5×22=12.
(2)原式=x2-y2-2x2+4y2=-x2+3y2.
当x=-1,y=时,原式=-(-1)2+3×()2=0
19. 解:由①得x≥1.
由②得x<4.
∴原不等式组的解集是1≤x<4,
∴原不等式组的所有的整数解是1、2、3.
20.解:(1)∵甲、乙、丙三种树每棵的价格之比是2∶2∶3,甲种树每棵200元,
∴乙种树每棵的价格200元,
丙种树每棵的价格200×=300(元).
(2)设购买乙种树x棵,则购买甲种树2x棵,购买丙种树(1 000-3x)棵,依题意得
200×2x+200×x+300(1 000-3x)=210 000.
解得x=300.
∴购买甲种树600棵,购买乙种树300棵,购买丙种树100棵.
(3)设若购买丙种树y棵,则购买甲、乙两种树共(1 000-y)棵,依题意得
200(1 000-y)+300y≤210 000+10 120.
解得y≤201.2.
∵y为正整数,
∴y=201.
∴丙种树最多可以购买201棵.
21.
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
22. (1)BD与AC的位置关系是:BD⊥AC,数量关系是BD=AC.理由如下:
如图1,延长BD交AC于点F.
( http: / / www.21cnjy.com )
∵AE⊥BC于E,∴∠BED=∠AEC=90°.
又∵AE=BE,DE=CE,∴△DBE≌△CAE,
∴BD=AC,∠DBE=∠CAE,∠BDE=∠ACE.
∵∠BDE=∠ADF,∴∠ADF=∠ACE.
∵∠ACE+∠CAE=90°,∴∠ADF+∠CAE=90°,
∴BD⊥AC.
(2)如图2,∵∠AEB=∠DEC=90°,
∴∠AEB+∠AED=∠DEC+∠AED,
即∠BED=∠AEC.
∵AE=BE,DE=CE,∴△BED≌△AEC,
∴BD=AC,∠BDE=∠ACE,∠DBE=∠CAE.
∵∠BFC=∠ACD+∠CDE+∠BDE=∠ACD+∠CDE+∠ACE=90°,
∴BD⊥AC.
(3)①BD与AC的数量关系是:BD=AC.
∵△ABE和△DCE是等边三角形,
∴∠AEB=∠ABE=60°,AE=BE,
∠DEC=∠DCE=60°,DE=CE,
∴∠AEB+∠AED=∠DEC+∠AED,
即∠BED=∠AEC,
∴△BED≌△AEC.
∴BD=AC.
②BD与AC的夹角度数为60°或120°.
同课章节目录
