第一章统计案例》回归分析的基本思想及其初步应用(二)(浙江省台州市路桥区)
文档属性
| 名称 | 第一章统计案例》回归分析的基本思想及其初步应用(二)(浙江省台州市路桥区) |

|
|
| 格式 | rar | ||
| 文件大小 | 25.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-11-16 00:00:00 | ||
图片预览



文档简介
课件12张PPT。回归分析的基本思想
及其初步应用(二)假设身高和随机误差的不同不会影响体重,
那么所有人的体重将相同,设8名女大学生
的体重是他们的平均体重54.5kg.由例1知,预报变量(体重)的值受
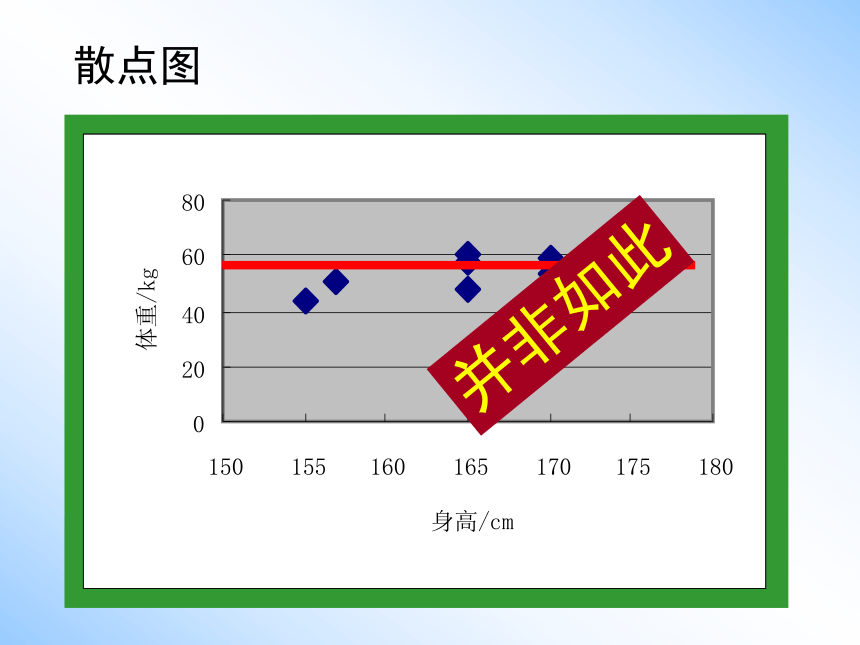
解释变量(身高)或随机误差的影响. 020406080150155160165170175180身高/cm体重/kg散点图并非如此为了刻画预报变量(体重)的变化在
多大程度上与解释变量(身高)有关?
在多大程度上与随机误差有关?我们引
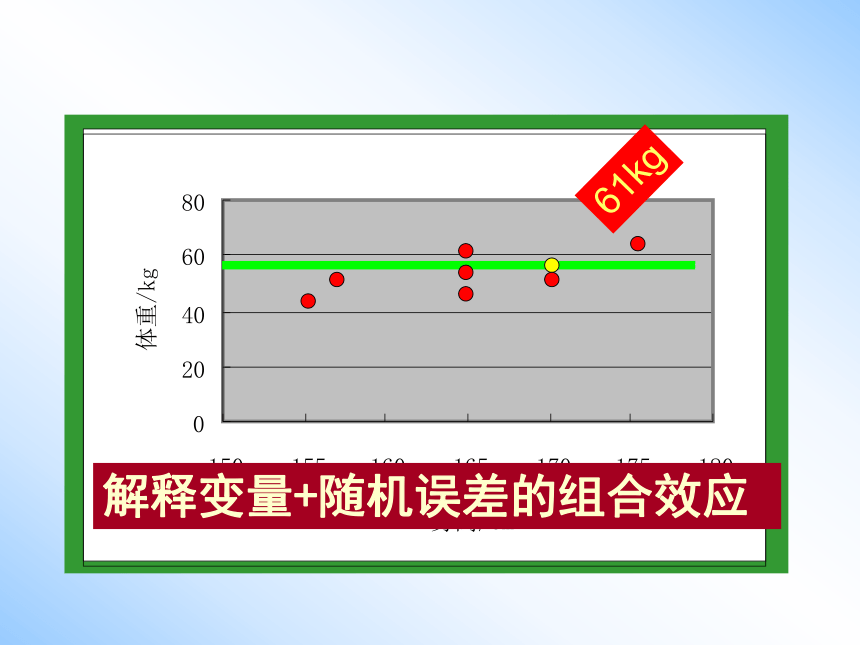
入了评价回归效果的三个统计量:总偏差平方和、残差平方和、回归平方和.020406080150155160165170175180身高/cm体重/kg61kg解释变量+随机误差的组合效应思考:
如何将这小效应合并在一个数中呢?把每个效应的平方加起来把这个总的效应称为总偏差平方和思考:在总效应中有多少来自解释变量,
有多少来自随机变量呢?所有的残差的平方后加起来,用数学符号表示为残差平方和 在研究两个变量间的关系时,首先要根
据散点图来粗略的判断他们是否线性相关,
是否可以用线性回归模型来拟合数据,然后
可以通过残差来判断模型拟合的效果,判断
原始数据中是否存在可疑数据,把这个工作
称为残差分析.例如:下表给出了女大学生身高和体重的原始数 据以及相应的残差数据分析:作残差图思考:我们用什么来刻画回归的效果呢?相关指数显然,R2的值越大,说明残差平方和越小,同时说明拟合效果越好,R2表示解释变量对预报变量变化的贡献率,R2越接近1,表示回归效果越好.建立回归模型的基本步骤:1.确定研究对象,明确解释变量,预报变量2.画散点图3.由经验确定回归方程的类型4.按一定规则估计回归方程中的参数5.得出结果分析残差图是否有一场,若存在异常,
则选择更合适的选变量 画散点图 选模型 估计参数 分析与预测例:关于x、y有如下数据为了对两个变量进行统计分析,现有以下两
种模型:试比较哪一个模型拟合的效果更好.
及其初步应用(二)假设身高和随机误差的不同不会影响体重,
那么所有人的体重将相同,设8名女大学生
的体重是他们的平均体重54.5kg.由例1知,预报变量(体重)的值受
解释变量(身高)或随机误差的影响. 020406080150155160165170175180身高/cm体重/kg散点图并非如此为了刻画预报变量(体重)的变化在
多大程度上与解释变量(身高)有关?
在多大程度上与随机误差有关?我们引
入了评价回归效果的三个统计量:总偏差平方和、残差平方和、回归平方和.020406080150155160165170175180身高/cm体重/kg61kg解释变量+随机误差的组合效应思考:
如何将这小效应合并在一个数中呢?把每个效应的平方加起来把这个总的效应称为总偏差平方和思考:在总效应中有多少来自解释变量,
有多少来自随机变量呢?所有的残差的平方后加起来,用数学符号表示为残差平方和 在研究两个变量间的关系时,首先要根
据散点图来粗略的判断他们是否线性相关,
是否可以用线性回归模型来拟合数据,然后
可以通过残差来判断模型拟合的效果,判断
原始数据中是否存在可疑数据,把这个工作
称为残差分析.例如:下表给出了女大学生身高和体重的原始数 据以及相应的残差数据分析:作残差图思考:我们用什么来刻画回归的效果呢?相关指数显然,R2的值越大,说明残差平方和越小,同时说明拟合效果越好,R2表示解释变量对预报变量变化的贡献率,R2越接近1,表示回归效果越好.建立回归模型的基本步骤:1.确定研究对象,明确解释变量,预报变量2.画散点图3.由经验确定回归方程的类型4.按一定规则估计回归方程中的参数5.得出结果分析残差图是否有一场,若存在异常,
则选择更合适的选变量 画散点图 选模型 估计参数 分析与预测例:关于x、y有如下数据为了对两个变量进行统计分析,现有以下两
种模型:试比较哪一个模型拟合的效果更好.
