初中数学北师大版九年级下册第二章 二次函数 说课课件(共20张PPT)
文档属性
| 名称 | 初中数学北师大版九年级下册第二章 二次函数 说课课件(共20张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-27 14:08:29 | ||
图片预览







文档简介
(共20张PPT)
北师大版九年级下册2.4
二次函数y=ax2+bx+c的图象
第1课时
说 课 内 容
教 材 分 析
教学任务分析
教 法 与 学 法
教学过程设计
本 节 课 特 点
学生情况分析
一、教材分析
关键词:
地位与作用
二次函数y=ax2+bx+c的图象是在学习了一次函数与反比例函数后的进一步学习,也是以后高中学习函数的重要基础。本课时的学习是学生在以往学习经验的基础上,尤其是已经学习了二次函数y=ax2+h的图像与特征后,进一步经历探索二次函数图象特征的过程。
让学生对二次函数y=a(x-h)2+k有一个形象和直观的认识。
二、学生情况分析
进入初三年级后,年级进行了数学走班分层教学。本节课面对的是C层的学生,C层学生的数学基础在40分左右。
关键词:
数学走班分层
基础较差、信心不足、兴趣不大。
三、教学任务分析
数学教学不仅是知识的教学,更应重视能力的培养及情感的教育。
知识目标:
1 能够正确作出二次函数y=a(x-h)2+k的图象;
2 理解二次函数关系式中系数a,h,k对函数图象的影响;
3 能够正确指出y=a(x-h)2+k的开口方向、对称轴和顶点坐标。
能力训练要求:
1、在精心设计的问题引领下,通过学生自己动手列表、描 点、连线,提高学生的作图能力;
2、通过观察图象,发现反比例函数的有关性质,训练学生的概括、总结能力;
3、通过小组合作,进一步培养学生的数学探究能力。
情感态度与价值观:
让学生积极参与到数学学习活动中,增强他们对数学学习的自信心,感受数学的美,从而激发学生的学习兴趣。
教学重难点:
能够正确作出y=a(x-h)2+k的图象,并抽象出它的图象特征。
四、教法与学法
把本节课内容细化为四大问题,逐一向学生提出。先鼓励学生自主学习(独学),再结合小组学习,通过“结对子”合作学习(对学)以及学习小组全体合作学习(群学) ,推导出结论。
问题引领、小组学习
关键词:
独学、对学与群学
让绝大多数学生参与到课程中去。
五、教学过程
(一)创设情境,引入新课
1、二次函数的图象是一条 。
2、二次函数y=2x2,y=2x2+1,y=2x2-5的图象有什么关系,它们是如何通过平移得到的?
3、上述的三个函数图象中,开口方向、对称轴和顶点坐标分别是什么?
(二)合作探讨,获得新知
问题一、在同一直角坐标系中,作出函数①y=x2和②y=(x-1)2{双数小组画y=(x+1)2}两个函数图象。
问题三、观察我们作出的三个函数图象,它们的开口方向,对称轴和顶点坐标分别是什么?它们的图象之间有什么关系呢?
问题二、在同一直角坐标系中作出函数③y=(x-1)2+2的图象{双数小组画y=(x+1)2} 。它又是什么样子的呢?
本节课总问题:怎样画出二次函数y=a(x-h)2+k的图象以及抽象出函数图象的特征。
问题四、二次函数y=a(x-h)2+k,它的开口方向、对称轴和顶点坐标分别是什么。
下一步骤:
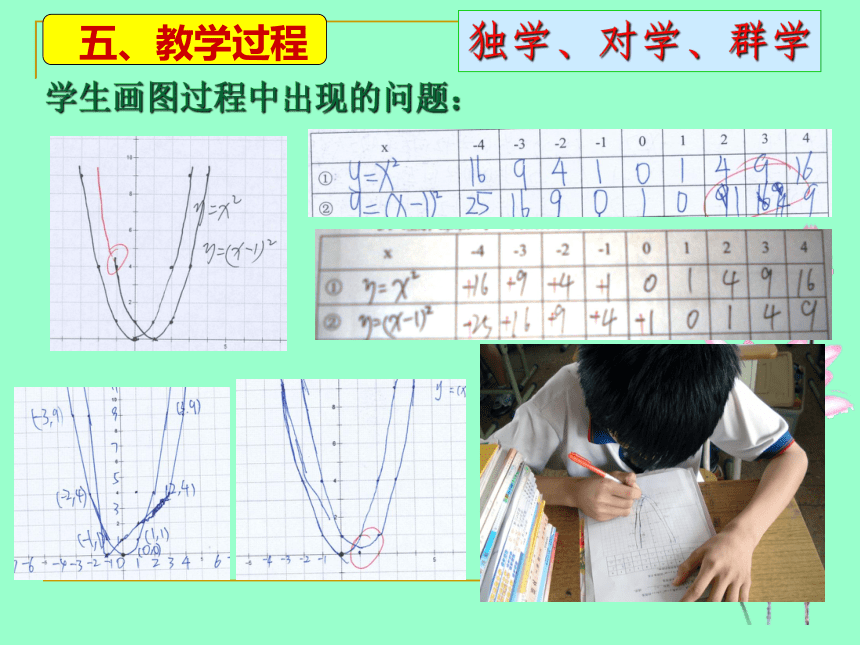
五、教学过程
学生画图过程中出现的问题:
五、教学过程
独学、对学、群学
五、教学过程
独学、对学、群学
学生画图过程中出现的问题:
数学学习是一种经验的学习
五、教学过程
独学、对学、群学
独学、对学、群学
五、教学过程
先独立猜测,再小组学习得出结论,老师引领归纳总结
五、教学过程
独学、对学、群学
y=a(x-h)2+k 开口方向 对称轴 顶点坐标
a>0 上 x=h (h,k)
a<0 下
(三)巩固练习
五、教学过程
指出下列二次函数的开口方向、对称轴和顶点坐标。指出是如何通过平移得到的。
(四)归纳总结
请同学们回顾作节课的内容,我们学到了什么呢?
图象特征:二次函数y=a(x-h)2+k的图象可以通过平移二次函数y=ax2的图象得到,因此它的开口方向、对称轴和顶点坐标与a,h,k的值有关。
五、教学过程
1、二次函数y=a(x-h)2+k的图象
2、二次函数y=a(x-h)2+k的开口方向、对称轴和顶点坐标与a,h,k之间的关系。
3、二次函数y=a(x-h)2+k与y=ax2的图象关系。
4、……
y=a(x-h)2+k 开口方向 对称轴 顶点坐标
a>0 上 x=h (h,k)
a<0 下
五、教学过程
(五)评价与反馈
5分钟小测:请画出y=-(x+4)2+2的图象,并指出它的开口方向、对称轴和顶点坐标。
(六)课后作业:书本P150 第1题
五、教学过程
关键词:
学有所得
获得荣誉
能力提高
增强自信心和学习兴趣
突出特点:
1.问题引领与小组学习。
3.自主学习、合作交流、大胆探索。
4.教师、学生的合理定位。
六、本节课特点
2.重难点细化分解,关注每一个学生。
2.4二次函数y=ax2+bx+c的图象
图象特征:
1 形状:
2 位置:
3
指出图象的开口、对称轴、顶点和位置平移关系
复习 引入
板书设计
函数 开口方向 对称轴 顶点 平移
y=x2
y=(x-1)2
y=(x-1)2+2
…
y=a(x-h)2+k 开口 对称轴 顶点
a>0 上 x=h (h,k)
a<0 下
敬请各位
专家指导!
北师大版九年级下册2.4
二次函数y=ax2+bx+c的图象
第1课时
说 课 内 容
教 材 分 析
教学任务分析
教 法 与 学 法
教学过程设计
本 节 课 特 点
学生情况分析
一、教材分析
关键词:
地位与作用
二次函数y=ax2+bx+c的图象是在学习了一次函数与反比例函数后的进一步学习,也是以后高中学习函数的重要基础。本课时的学习是学生在以往学习经验的基础上,尤其是已经学习了二次函数y=ax2+h的图像与特征后,进一步经历探索二次函数图象特征的过程。
让学生对二次函数y=a(x-h)2+k有一个形象和直观的认识。
二、学生情况分析
进入初三年级后,年级进行了数学走班分层教学。本节课面对的是C层的学生,C层学生的数学基础在40分左右。
关键词:
数学走班分层
基础较差、信心不足、兴趣不大。
三、教学任务分析
数学教学不仅是知识的教学,更应重视能力的培养及情感的教育。
知识目标:
1 能够正确作出二次函数y=a(x-h)2+k的图象;
2 理解二次函数关系式中系数a,h,k对函数图象的影响;
3 能够正确指出y=a(x-h)2+k的开口方向、对称轴和顶点坐标。
能力训练要求:
1、在精心设计的问题引领下,通过学生自己动手列表、描 点、连线,提高学生的作图能力;
2、通过观察图象,发现反比例函数的有关性质,训练学生的概括、总结能力;
3、通过小组合作,进一步培养学生的数学探究能力。
情感态度与价值观:
让学生积极参与到数学学习活动中,增强他们对数学学习的自信心,感受数学的美,从而激发学生的学习兴趣。
教学重难点:
能够正确作出y=a(x-h)2+k的图象,并抽象出它的图象特征。
四、教法与学法
把本节课内容细化为四大问题,逐一向学生提出。先鼓励学生自主学习(独学),再结合小组学习,通过“结对子”合作学习(对学)以及学习小组全体合作学习(群学) ,推导出结论。
问题引领、小组学习
关键词:
独学、对学与群学
让绝大多数学生参与到课程中去。
五、教学过程
(一)创设情境,引入新课
1、二次函数的图象是一条 。
2、二次函数y=2x2,y=2x2+1,y=2x2-5的图象有什么关系,它们是如何通过平移得到的?
3、上述的三个函数图象中,开口方向、对称轴和顶点坐标分别是什么?
(二)合作探讨,获得新知
问题一、在同一直角坐标系中,作出函数①y=x2和②y=(x-1)2{双数小组画y=(x+1)2}两个函数图象。
问题三、观察我们作出的三个函数图象,它们的开口方向,对称轴和顶点坐标分别是什么?它们的图象之间有什么关系呢?
问题二、在同一直角坐标系中作出函数③y=(x-1)2+2的图象{双数小组画y=(x+1)2} 。它又是什么样子的呢?
本节课总问题:怎样画出二次函数y=a(x-h)2+k的图象以及抽象出函数图象的特征。
问题四、二次函数y=a(x-h)2+k,它的开口方向、对称轴和顶点坐标分别是什么。
下一步骤:
五、教学过程
学生画图过程中出现的问题:
五、教学过程
独学、对学、群学
五、教学过程
独学、对学、群学
学生画图过程中出现的问题:
数学学习是一种经验的学习
五、教学过程
独学、对学、群学
独学、对学、群学
五、教学过程
先独立猜测,再小组学习得出结论,老师引领归纳总结
五、教学过程
独学、对学、群学
y=a(x-h)2+k 开口方向 对称轴 顶点坐标
a>0 上 x=h (h,k)
a<0 下
(三)巩固练习
五、教学过程
指出下列二次函数的开口方向、对称轴和顶点坐标。指出是如何通过平移得到的。
(四)归纳总结
请同学们回顾作节课的内容,我们学到了什么呢?
图象特征:二次函数y=a(x-h)2+k的图象可以通过平移二次函数y=ax2的图象得到,因此它的开口方向、对称轴和顶点坐标与a,h,k的值有关。
五、教学过程
1、二次函数y=a(x-h)2+k的图象
2、二次函数y=a(x-h)2+k的开口方向、对称轴和顶点坐标与a,h,k之间的关系。
3、二次函数y=a(x-h)2+k与y=ax2的图象关系。
4、……
y=a(x-h)2+k 开口方向 对称轴 顶点坐标
a>0 上 x=h (h,k)
a<0 下
五、教学过程
(五)评价与反馈
5分钟小测:请画出y=-(x+4)2+2的图象,并指出它的开口方向、对称轴和顶点坐标。
(六)课后作业:书本P150 第1题
五、教学过程
关键词:
学有所得
获得荣誉
能力提高
增强自信心和学习兴趣
突出特点:
1.问题引领与小组学习。
3.自主学习、合作交流、大胆探索。
4.教师、学生的合理定位。
六、本节课特点
2.重难点细化分解,关注每一个学生。
2.4二次函数y=ax2+bx+c的图象
图象特征:
1 形状:
2 位置:
3
指出图象的开口、对称轴、顶点和位置平移关系
复习 引入
板书设计
函数 开口方向 对称轴 顶点 平移
y=x2
y=(x-1)2
y=(x-1)2+2
…
y=a(x-h)2+k 开口 对称轴 顶点
a>0 上 x=h (h,k)
a<0 下
敬请各位
专家指导!
