5.1轴对称 课件(共45张PPT)2023-2024学年湘教版数学七年级下册
文档属性
| 名称 | 5.1轴对称 课件(共45张PPT)2023-2024学年湘教版数学七年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 5.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-27 15:10:27 | ||
图片预览







文档简介
(共45张PPT)
5.1 轴对称
5.1.1 轴对称图形
湘教版数学七年级下册
第5章 轴对称与旋转
情境导入
观察下列图片和图形,它们有什么共同特点?
折一折,剪一剪素材
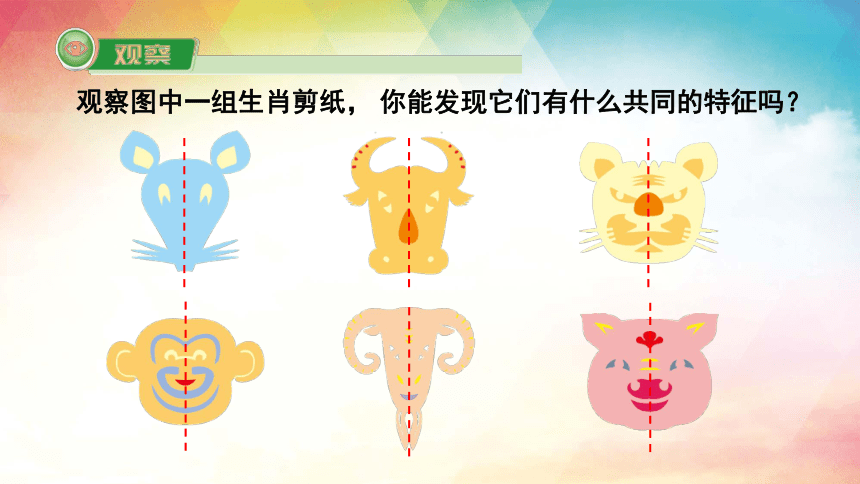
观察图中一组生肖剪纸, 你能发现它们有什么共同的特征吗?
如果一个平面图形沿一条直线折叠后, 直线两侧的部分能够互相重合,那么这个图形叫做轴对称图形,这条直线叫做它的对称轴.
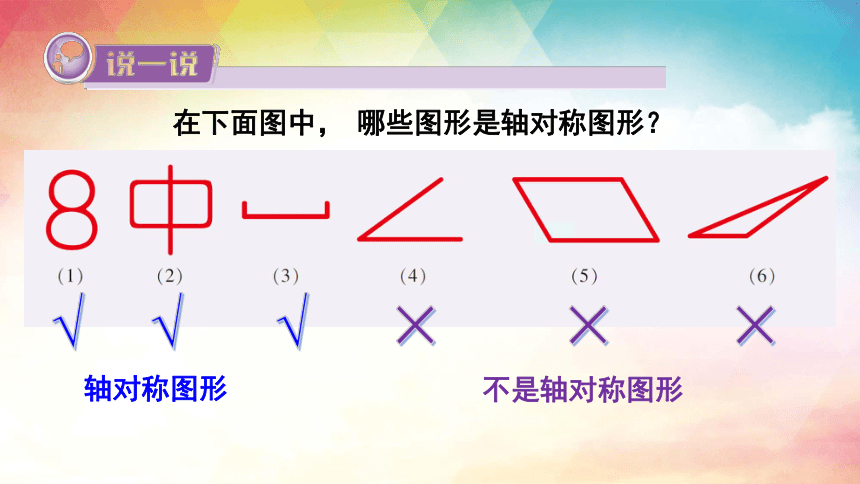
在下面图中, 哪些图形是轴对称图形?
√
√
√
轴对称图形
×
×
×
不是轴对称图形
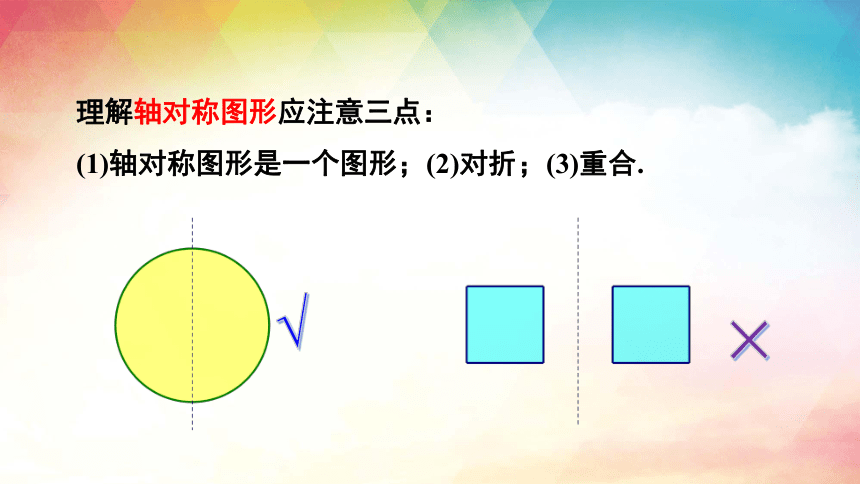
理解轴对称图形应注意三点:
(1)轴对称图形是一个图形;(2)对折;(3)重合.
√
×
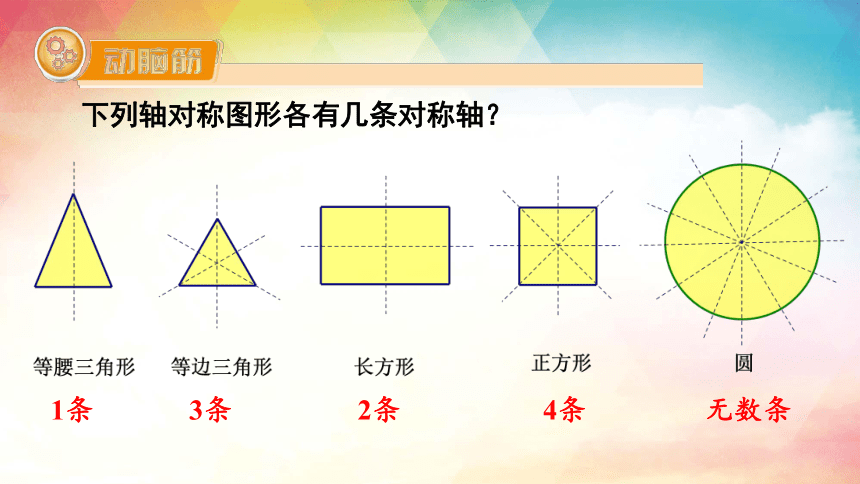
下列轴对称图形各有几条对称轴?
1条
3条
2条
4条
无数条
练 习
[选自教材P114 练习]
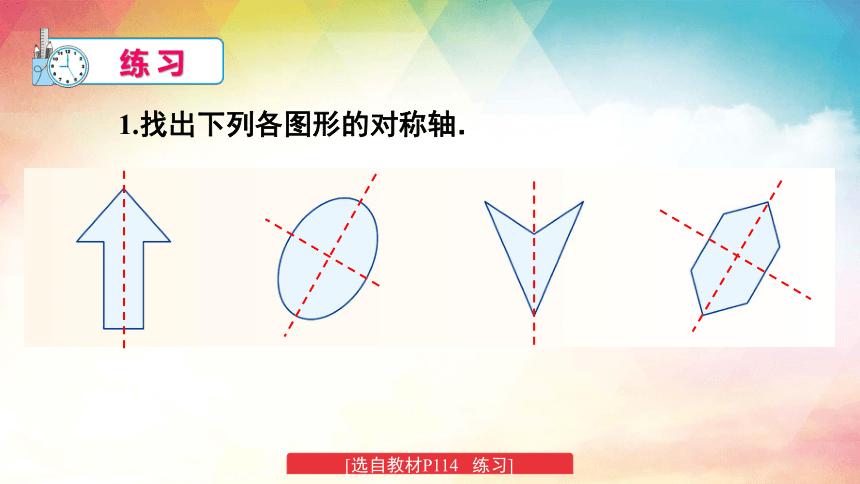
1.找出下列各图形的对称轴.
[选自教材P114 练习]
2.举出生活中一些轴对称图形的实例.
练 习
随堂演练
1.如图所示的几个图案中,是轴对称图形的是( )
A
2.如图所示,下面的 5 个英文字母中是轴对称图形的有( )
A. 2个 B. 3个 C. 4个 D. 5个
√
√
√
B
3. 如图所示的图案中,是轴对称图形的有( )
A. 1个 B. 2个
C. 3个 D. 4个
√
√
B
4. 如图所示,从轴对称的角度来看,你觉得下面哪一个图形比较独特?简单说明你的理由.
解:(3)比较独特,它有无数条对称轴,其他图形只有两条对称轴.
5. 观察如图所示的图案,它们都是轴对称图形,它们各有几条对称轴?在图中画出所有的对称轴.
解:(1)2条,(2)4条, (3)5条, (4)3条.
6.你认识世界上各国的国旗吗?如图所示,观察下面的一些国家的国旗,是轴对称图形的有( ).
甲、乙、丙、戊
7. 如图所示的四个图形中,从几何图形的性质考虑哪一个与其他三个不同?请指出这个图形,并简述你的理由.
解:②;不是轴对称图形.
课堂小结
如果一个平面图形沿一条直线折叠后, 直线两侧的部分能够互相重合,那么这个图形叫做轴对称图形,这条直线叫做它的对称轴.
5.1 轴对称
5.1.2 轴对称变换
湘教版数学七年级下册
第5章 轴对称与旋转
复习回顾
说一说什么是轴对称图形?
如果一个平面图形沿一条直线折叠后, 直线两侧的部分能够互相重合,那么这个图形叫做轴对称图形,这条直线叫做它的对称轴.
观察:在一张纸上盖上一个印,趁油墨未干之时,将纸张沿着直线 l 对折,得到一个图形,随后打开纸张展平,观察两图形会有怎样的现象?
l
(a)
(b)
l
把图形(a)沿着直线 l 翻折并将图形“复印” 下来得到图形(b),就叫做该图形关于直线 l 作了轴对称变换,也叫轴反射.
原像
像
如果一个图形关于某一条直线作轴对称变换后,能够与另一个图形重合,那么这两个图形关于这条直线对称,也称两个图形成轴对称.
l
(a)
(b)
(a)
(b)
l
点 A′ 是 A 的对应点
对称轴 l 两边的图形(a)与(b)的形状和大小发生变化了吗?
(a)
(b)
l
轴对称变换不改变图形的形状和大小.
三角形 ABC 和三角形 A′B′C′ 关于直线 l 成轴对称,点 P 和 P′ 是对应点,线段 PP′ 交直线 l 于点 D. 那么线段 PP′ 与对称轴 l 有什么关系呢?
成轴对称的两个图形中,对应点的连线被对称轴垂直平分.
PD = _____,∠1=____ = ____°
P′D
∠2
90
点 P 与点 P′ 重合
如果两个图形的对应点的连线被同一条直线垂直平分,那么这两个图形关于这条直线对称.
已知直线 l 及直线外一点 P,求作点 P′, 使它与点 P 关于直线 l 对称.
作法:
1. 过点 P 作 PQ⊥l, 交 l 于点 O.
2. 在直线 PQ 上, 截取 OP′= OP.
则点 P′ 即为所求作的点.
已知线段 AB 和直线 l,作出与线段 AB 关于直线 l 对称的图形.
作法:
1.过点 A 作直线 l 的垂线,垂足为点O,延长AO至点A′,使AO = A′O, 点 A′ 就是点 A 关于直线 l 的对称点;
2.类似地,作出点 B 关于直线 l 的对称点 B′.
3.连接A′B′ .
作已知图形关于已知直线对称的图形的一般步骤:
1.找点(确定图形中的一些特殊点);
2.画点(画出特殊点关于已知直线的对称点);
3.连线(连接对称点).
已知三角形 ABC 和直线 l,作出与三角形 ABC 关于直线 l 对称的图形.
作法: 1. 过点 A 作直线 l 的垂线,垂足为点 O,在垂线上截取 OA′ = OA,点 A′ 就是点 A 关于直线 l 的对应点.
2. 类似地,分别作出点 B,C 关于直线 l 的对应点 B′,C′.
3. 连接 A′B′,B′C′,C′A′ 得到的三角形 A′B′C′ 即为所求.
翻折动画
联系:把成轴对称的两个图形看成一个整体,它就是一个轴对称图形;
把一个轴对称图形沿对称轴分成两个图形,这两个图形关于这条直线轴对称.
轴对称与轴对称图形两者之间的联系?
相同点:都是关于某一条直线折叠,两部分重合。
不同点:轴对称是两个图形。
轴对称图形是一个图形。
练 习
[选自教材P117 练习]
1. 举出生活中一些成轴对称的实例.
[选自教材P117 练习]
2. 下列三个图案分别成轴对称吗?如果是,画出它们的对称轴,并标出一对对应点.
随堂演练
1.下列说法错误的是( )
A.等边三角形是轴对称图形
B.轴对称图形的对应边相等, 对应角相等
C.成轴对称的两条线段必在对称轴一侧
D.成轴对称的两个图形对应点的连线被对称轴垂直平分
C
2.将一张矩形纸对折,用圆规针尖扎出一个“∑”符号,然后将纸打开后铺平.
(2)在扎出∑的过程中,点 A与____重合,点B与____重合,点C与C′重合;线段AB与____重合,线段BC与____重合,∠OAB与________重合,∠ABC与__________重合.
∴线段AB___线段A′B′,线段BC___线段B′C′,∠OAB___∠O′A′B′,∠ABC___∠A′B′C′.(以上四空填“=”或“≠”)
(1)图中两个“∑”关于折痕 l_______.
对称
A′
B′
∠O′A′B′
A′B′
B′C′
∠A′B′C′
=
=
=
=
3. 在下列方格纸上画出关于直线 l 对称的图形.
4.如图,已知三角形 ABC 和直线 MN. 求作:三角形 A′B′C′,使三角形 A′B′C′ 和三角形 ABC 关于直线 MN 对称.
N
N
5.如图,∠AOB 内一点 P,P1、P2 分别是 P 关于OA、OB的对称点,P1P2 交 OA 于 M,交 OB 于 N,若 P1P2 = 5 cm,求三角形 PMN 的周长.
解:∵点 P1是点 P 关于 OA 的对称点,
∴OA垂直平分PP1,则 P1M = PM,
同样道理 P2N = PN,
这样三角形 PMN 的周长
PM + MN + NP = P1M + MN + NP2 = P1P2 = 5 cm.
6.如图,三角形ABC和三角形A′B′C′关于直线m对称.
(1)结合图形指出对应点.
(2)连接A、A′,直线m与线段AA′有什么关系?
(3)延长线段AC与A′C′,它们的交点与直线m有怎样的关系?其他对应线段(或其延长线)的交点呢?你发现了什么规律,请叙述出来与同伴交流.
解:(1)A和A′,B和B′,C和C′是对应点;
(2)m垂直平分线段AA′;
(3)两个图形关于某条直线对称,如果它们的对应线段或延长线相交,那么交点在对称轴上.
课堂小结
轴对称变换不改变图形的形状和大小.
成轴对称的两个图形中,对应点的连线被对称轴垂直平分.
谢谢观看
5.1 轴对称
5.1.1 轴对称图形
湘教版数学七年级下册
第5章 轴对称与旋转
情境导入
观察下列图片和图形,它们有什么共同特点?
折一折,剪一剪素材
观察图中一组生肖剪纸, 你能发现它们有什么共同的特征吗?
如果一个平面图形沿一条直线折叠后, 直线两侧的部分能够互相重合,那么这个图形叫做轴对称图形,这条直线叫做它的对称轴.
在下面图中, 哪些图形是轴对称图形?
√
√
√
轴对称图形
×
×
×
不是轴对称图形
理解轴对称图形应注意三点:
(1)轴对称图形是一个图形;(2)对折;(3)重合.
√
×
下列轴对称图形各有几条对称轴?
1条
3条
2条
4条
无数条
练 习
[选自教材P114 练习]
1.找出下列各图形的对称轴.
[选自教材P114 练习]
2.举出生活中一些轴对称图形的实例.
练 习
随堂演练
1.如图所示的几个图案中,是轴对称图形的是( )
A
2.如图所示,下面的 5 个英文字母中是轴对称图形的有( )
A. 2个 B. 3个 C. 4个 D. 5个
√
√
√
B
3. 如图所示的图案中,是轴对称图形的有( )
A. 1个 B. 2个
C. 3个 D. 4个
√
√
B
4. 如图所示,从轴对称的角度来看,你觉得下面哪一个图形比较独特?简单说明你的理由.
解:(3)比较独特,它有无数条对称轴,其他图形只有两条对称轴.
5. 观察如图所示的图案,它们都是轴对称图形,它们各有几条对称轴?在图中画出所有的对称轴.
解:(1)2条,(2)4条, (3)5条, (4)3条.
6.你认识世界上各国的国旗吗?如图所示,观察下面的一些国家的国旗,是轴对称图形的有( ).
甲、乙、丙、戊
7. 如图所示的四个图形中,从几何图形的性质考虑哪一个与其他三个不同?请指出这个图形,并简述你的理由.
解:②;不是轴对称图形.
课堂小结
如果一个平面图形沿一条直线折叠后, 直线两侧的部分能够互相重合,那么这个图形叫做轴对称图形,这条直线叫做它的对称轴.
5.1 轴对称
5.1.2 轴对称变换
湘教版数学七年级下册
第5章 轴对称与旋转
复习回顾
说一说什么是轴对称图形?
如果一个平面图形沿一条直线折叠后, 直线两侧的部分能够互相重合,那么这个图形叫做轴对称图形,这条直线叫做它的对称轴.
观察:在一张纸上盖上一个印,趁油墨未干之时,将纸张沿着直线 l 对折,得到一个图形,随后打开纸张展平,观察两图形会有怎样的现象?
l
(a)
(b)
l
把图形(a)沿着直线 l 翻折并将图形“复印” 下来得到图形(b),就叫做该图形关于直线 l 作了轴对称变换,也叫轴反射.
原像
像
如果一个图形关于某一条直线作轴对称变换后,能够与另一个图形重合,那么这两个图形关于这条直线对称,也称两个图形成轴对称.
l
(a)
(b)
(a)
(b)
l
点 A′ 是 A 的对应点
对称轴 l 两边的图形(a)与(b)的形状和大小发生变化了吗?
(a)
(b)
l
轴对称变换不改变图形的形状和大小.
三角形 ABC 和三角形 A′B′C′ 关于直线 l 成轴对称,点 P 和 P′ 是对应点,线段 PP′ 交直线 l 于点 D. 那么线段 PP′ 与对称轴 l 有什么关系呢?
成轴对称的两个图形中,对应点的连线被对称轴垂直平分.
PD = _____,∠1=____ = ____°
P′D
∠2
90
点 P 与点 P′ 重合
如果两个图形的对应点的连线被同一条直线垂直平分,那么这两个图形关于这条直线对称.
已知直线 l 及直线外一点 P,求作点 P′, 使它与点 P 关于直线 l 对称.
作法:
1. 过点 P 作 PQ⊥l, 交 l 于点 O.
2. 在直线 PQ 上, 截取 OP′= OP.
则点 P′ 即为所求作的点.
已知线段 AB 和直线 l,作出与线段 AB 关于直线 l 对称的图形.
作法:
1.过点 A 作直线 l 的垂线,垂足为点O,延长AO至点A′,使AO = A′O, 点 A′ 就是点 A 关于直线 l 的对称点;
2.类似地,作出点 B 关于直线 l 的对称点 B′.
3.连接A′B′ .
作已知图形关于已知直线对称的图形的一般步骤:
1.找点(确定图形中的一些特殊点);
2.画点(画出特殊点关于已知直线的对称点);
3.连线(连接对称点).
已知三角形 ABC 和直线 l,作出与三角形 ABC 关于直线 l 对称的图形.
作法: 1. 过点 A 作直线 l 的垂线,垂足为点 O,在垂线上截取 OA′ = OA,点 A′ 就是点 A 关于直线 l 的对应点.
2. 类似地,分别作出点 B,C 关于直线 l 的对应点 B′,C′.
3. 连接 A′B′,B′C′,C′A′ 得到的三角形 A′B′C′ 即为所求.
翻折动画
联系:把成轴对称的两个图形看成一个整体,它就是一个轴对称图形;
把一个轴对称图形沿对称轴分成两个图形,这两个图形关于这条直线轴对称.
轴对称与轴对称图形两者之间的联系?
相同点:都是关于某一条直线折叠,两部分重合。
不同点:轴对称是两个图形。
轴对称图形是一个图形。
练 习
[选自教材P117 练习]
1. 举出生活中一些成轴对称的实例.
[选自教材P117 练习]
2. 下列三个图案分别成轴对称吗?如果是,画出它们的对称轴,并标出一对对应点.
随堂演练
1.下列说法错误的是( )
A.等边三角形是轴对称图形
B.轴对称图形的对应边相等, 对应角相等
C.成轴对称的两条线段必在对称轴一侧
D.成轴对称的两个图形对应点的连线被对称轴垂直平分
C
2.将一张矩形纸对折,用圆规针尖扎出一个“∑”符号,然后将纸打开后铺平.
(2)在扎出∑的过程中,点 A与____重合,点B与____重合,点C与C′重合;线段AB与____重合,线段BC与____重合,∠OAB与________重合,∠ABC与__________重合.
∴线段AB___线段A′B′,线段BC___线段B′C′,∠OAB___∠O′A′B′,∠ABC___∠A′B′C′.(以上四空填“=”或“≠”)
(1)图中两个“∑”关于折痕 l_______.
对称
A′
B′
∠O′A′B′
A′B′
B′C′
∠A′B′C′
=
=
=
=
3. 在下列方格纸上画出关于直线 l 对称的图形.
4.如图,已知三角形 ABC 和直线 MN. 求作:三角形 A′B′C′,使三角形 A′B′C′ 和三角形 ABC 关于直线 MN 对称.
N
N
5.如图,∠AOB 内一点 P,P1、P2 分别是 P 关于OA、OB的对称点,P1P2 交 OA 于 M,交 OB 于 N,若 P1P2 = 5 cm,求三角形 PMN 的周长.
解:∵点 P1是点 P 关于 OA 的对称点,
∴OA垂直平分PP1,则 P1M = PM,
同样道理 P2N = PN,
这样三角形 PMN 的周长
PM + MN + NP = P1M + MN + NP2 = P1P2 = 5 cm.
6.如图,三角形ABC和三角形A′B′C′关于直线m对称.
(1)结合图形指出对应点.
(2)连接A、A′,直线m与线段AA′有什么关系?
(3)延长线段AC与A′C′,它们的交点与直线m有怎样的关系?其他对应线段(或其延长线)的交点呢?你发现了什么规律,请叙述出来与同伴交流.
解:(1)A和A′,B和B′,C和C′是对应点;
(2)m垂直平分线段AA′;
(3)两个图形关于某条直线对称,如果它们的对应线段或延长线相交,那么交点在对称轴上.
课堂小结
轴对称变换不改变图形的形状和大小.
成轴对称的两个图形中,对应点的连线被对称轴垂直平分.
谢谢观看
