24.6正多边形与圆 课件(共36张PPT)2023-2024学年 沪科版数学九年级下册
文档属性
| 名称 | 24.6正多边形与圆 课件(共36张PPT)2023-2024学年 沪科版数学九年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-27 00:00:00 | ||
图片预览







文档简介
(共36张PPT)
24.6 正多边形与圆
第1课时 正多边形与圆
沪科版数学九年级下册
第24章 圆
新课导入
观察下列图形,说说你的发现.
新课推进
正三角形
三条边相等,
三个角相等(60°)
四条边相等,
四个角相等(90°)
正方形
正多边形定义
各边相等、各角也相等的多边形叫做正多边形.
正n边形:如果一个正多边形有n条边, 那么这个正多边形叫做正n边形.
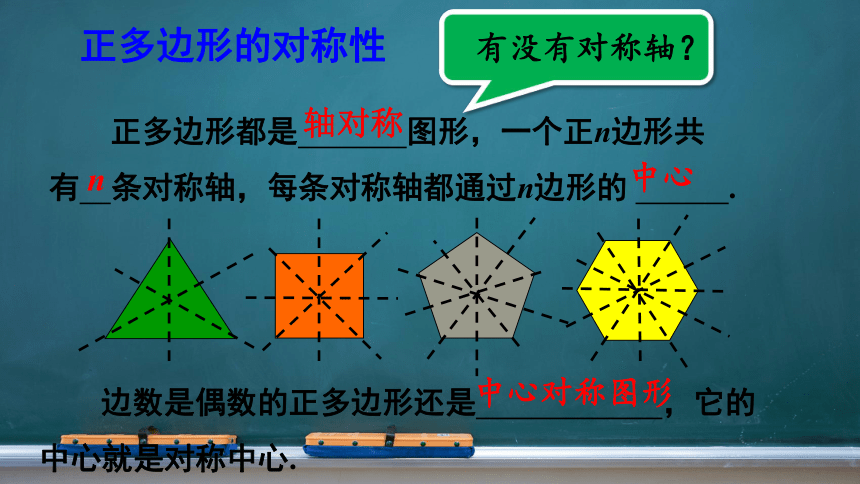
正多边形都是 图形,一个正n边形共有 条对称轴,每条对称轴都通过n边形的 .
正多边形的对称性
边数是偶数的正多边形还是 ,它的中心就是对称中心.
轴对称
n
中心
中心对称图形
有没有对称轴?
你知道正多边形与圆的关系吗?
思 考
正多边形和圆的关系非常密切,只要把一个圆分成相等的一些弧,就可以作出这个圆的内接或外切正多边形,这个圆就是这个正多边形的外接圆或内切圆.
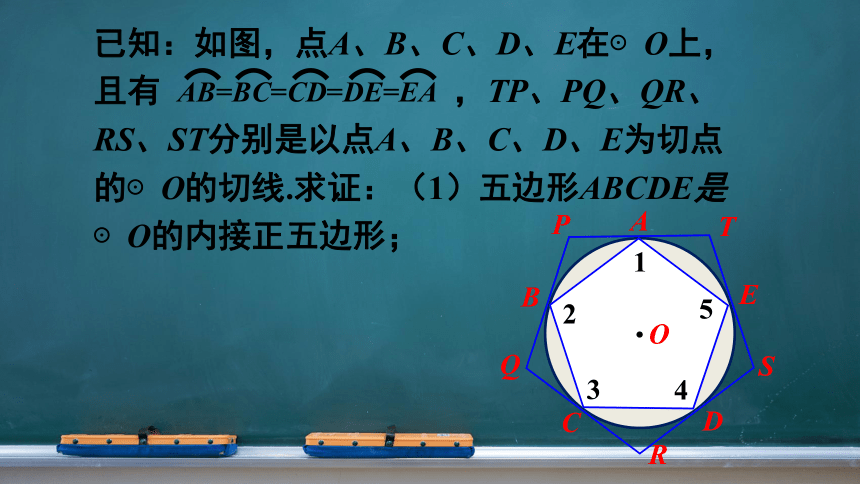
已知:如图,点A、B、C、D、E在⊙O上,且有 ,TP、PQ、QR、RS、ST分别是以点A、B、C、D、E为切点的⊙O的切线.求证:(1)五边形ABCDE是⊙O的内接正五边形;
AB=BC=CD=DE=EA
︵
︵
︵
︵
︵
A
B
C
D
E
O
P
Q
R
S
T
1
2
3
4
5
A
B
C
D
E
O
P
Q
R
S
T
1
2
3
4
5
∴ AB=BC=CD=DE=EA,
∴ ∠1=∠2.
同理∠2=∠3=∠4=∠5.
又五边形ABCDE的顶点都在⊙O上,
∴ 五边形ABCDE是⊙O的内接正五边形,
⊙O是五边形ABCD的外接圆.
证明:
AB=BC=CD=DE=EA,
︵
︵
︵
︵
︵
∵
∴ BCE=CDA=3AB,
︵
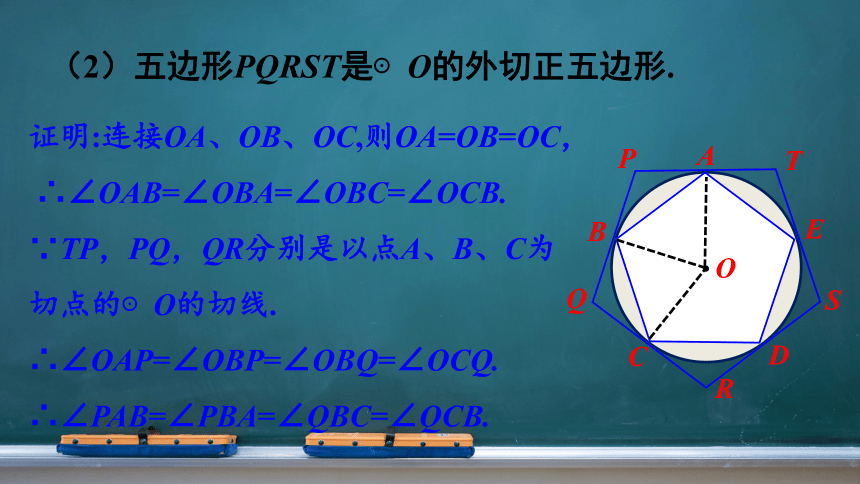
(2)五边形PQRST是⊙O的外切正五边形.
证明:连接OA、OB、OC,则OA=OB=OC,
∴∠OAB=∠OBA=∠OBC=∠OCB.
∵TP,PQ,QR分别是以点A、B、C为
切点的⊙O的切线.
∴∠OAP=∠OBP=∠OBQ=∠OCQ.
∴∠PAB=∠PBA=∠QBC=∠QCB.
A
B
C
D
E
O
P
Q
R
S
T
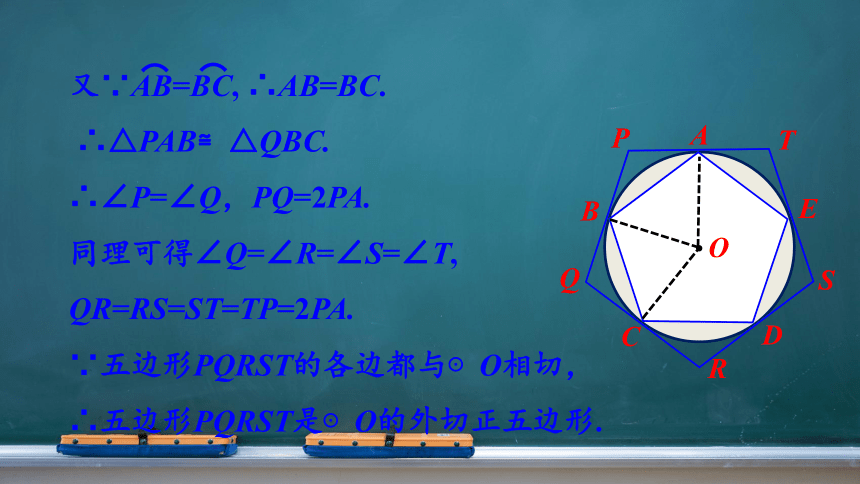
又∵AB=BC, ∴AB=BC.
∴△PAB≌△QBC.
∴∠P=∠Q,PQ=2PA.
同理可得∠Q=∠R=∠S=∠T,
QR=RS=ST=TP=2PA.
∵五边形PQRST的各边都与⊙O相切,
∴五边形PQRST是⊙O的外切正五边形.
A
B
C
D
E
O
P
Q
R
S
T
︵
︵
有关正多边形的作图
(1)用量角器等分圆周
已知⊙O的半径为2cm,求作圆的内接正三角形.
120°
A
O
C
B
用量角器度量,使∠AOB=
∠BOC=∠COA=120°.
正五角星的作法
72°
(2)用尺规等分圆周
用直尺和圆规作⊙O的两条互相垂直的直径,就可以把⊙O等分成4等份,从而作出正四边形.
正八边形的作法
在正四边形的基础上,我们再逐次平分各边所对的弧,就可以作出正八边形.
想一想:正十六边形怎么作?
正六边形的作法
设⊙O的半径为R,通常先作出⊙O的一条直径AB,然后分别以点A,B为圆心、R为半径作弧,与⊙O交于点C,D,E,F,从而得到⊙O的6等份点.
O
A
B
C
D
E
F
1.下列说法中正确的是( )
A.各边都相等的多边形是正多边形
B.正多边形既是轴对称图形,又是中心对称图形
C.各边都相等的圆内接多边形是正多边形
D.各角都相等的圆内接多边形是正多边形
C
随堂演练
2.如果一个正多边形的每个外角都等于36°,则这个多边形的中心角等于( )
A.36° B.18° C.72° D.54°
A
3.如图,点O是正六边形的对称中心,如果用一副三角板的角,借助点O(使直角的顶点落在点O处),把这个正六边形的面积n等分,那么n的所有可能取值的个数是( )
A.4 B.5 C.6 D.7
B
24.6 正多边形与圆
第2课时 正多边形的性质
沪科版数学九年级下册
第24章 圆
思 考
将一个圆n等分,就可以作出这个圆的内接或外切正n边形,反过来,是不是每个正多边形都有一个外接圆和一个内切圆呢?
我们仍然以五边形为例来进行研究.
如图,过正五边形ABCDE的顶点A,B,C作⊙O,连结OA,OB,OC,OD,OE.
∵ OB=OC,
∴ ∠OBC=∠OCB.
又 ∵ ∠ABC=∠BCD,
∴ ∠OBA=∠OCD.
A
B
C
D
E
O
新课推进
∵ AB=DC,
∴ △OAB≌△ODC.
∴ OA=OD,
即点D在⊙O上.
同理,得点E也在⊙O上.
所以正五边形ABCDE有一个以O为圆心的外接圆.
A
B
C
D
E
O
由于正五边形ABCDE的各边是⊙O中相等的弦,等弦的弦心距相等,所以以点O为圆心、弦心距OH为半径的圆与正五边形的各边都相切.
因而,正五边形ABCDE还有一个以O为圆心的内切圆.
A
B
C
D
E
O
H
任何正多边形都有一个外接圆和一个内切圆,并且这两个圆是同心圆.
正多边形的有关概念及相关计算
E
F
C
D
.
O
中心角
半径R
边心距r
正多边形的中心:该正多边形的外接圆和内切圆的公共圆心.
正多边形的半径:外接圆的半径.
正多边形的中心角:正多边形的每一条边所对的圆心角.
正多边形的边心距:内切圆的半径.
A
B
正n边形的一个内角的
度数是____________;
中心角是___________;
正多边形的中心角与外角的
大小关系是________.
中心角与内角互补.
相等
想一想:
E
D
C
B
A
O
F
正多边形都是轴对称图形,一个正n边形共有n条对称轴,每条对称轴都通过n边形的中心.
如果一个正多边形有偶数条边,那么它又是中心对称图形,它的中心就是对称中心.
例 求边长为a的正六边形的周长和面积.
解 如图,过正六边形的中心O作OG⊥BC,垂足是G,连接OB,OC,设该正六边形的周长和面积分别为C和S.
∵ 多边形ABCDEF是正六边形,
∴ ∠BOC=60°,△BOC是等边三角形.
∴ C=6BC=6a.
A
B
C
D
E
F
O
G
在△BOC中,有
A
B
C
D
E
F
O
G
1. 如图,要拧开一个边长为a=6mm的正六边形螺帽,扳手张开的开口b至少为多少?
随堂演练
解:如图,∠ABC=120°. AB=BC=a, AC=b.
过B作BD⊥AC于点D,
则AD=DC= b.
在Rt△ABD中,∠BAC=30°,
∴BD= AB=3mm.
∴b=2AD=6 mm.
即扳手张开的开口b至少要6 mm.
A
C
B D
2. 求出半径为R的圆内接正三角形的边长,边心距和面积.
解:作等边△ABC的BC边上的高AD,垂足为D
·
A
B
C
D
O
连接OB,则OB=R
在Rt△OBD中∠OBD=30°,
边心距=OD=
在Rt△ABD中∠BAD=30°,
·
A
B
C
D
O
谢谢观看
24.6 正多边形与圆
第1课时 正多边形与圆
沪科版数学九年级下册
第24章 圆
新课导入
观察下列图形,说说你的发现.
新课推进
正三角形
三条边相等,
三个角相等(60°)
四条边相等,
四个角相等(90°)
正方形
正多边形定义
各边相等、各角也相等的多边形叫做正多边形.
正n边形:如果一个正多边形有n条边, 那么这个正多边形叫做正n边形.
正多边形都是 图形,一个正n边形共有 条对称轴,每条对称轴都通过n边形的 .
正多边形的对称性
边数是偶数的正多边形还是 ,它的中心就是对称中心.
轴对称
n
中心
中心对称图形
有没有对称轴?
你知道正多边形与圆的关系吗?
思 考
正多边形和圆的关系非常密切,只要把一个圆分成相等的一些弧,就可以作出这个圆的内接或外切正多边形,这个圆就是这个正多边形的外接圆或内切圆.
已知:如图,点A、B、C、D、E在⊙O上,且有 ,TP、PQ、QR、RS、ST分别是以点A、B、C、D、E为切点的⊙O的切线.求证:(1)五边形ABCDE是⊙O的内接正五边形;
AB=BC=CD=DE=EA
︵
︵
︵
︵
︵
A
B
C
D
E
O
P
Q
R
S
T
1
2
3
4
5
A
B
C
D
E
O
P
Q
R
S
T
1
2
3
4
5
∴ AB=BC=CD=DE=EA,
∴ ∠1=∠2.
同理∠2=∠3=∠4=∠5.
又五边形ABCDE的顶点都在⊙O上,
∴ 五边形ABCDE是⊙O的内接正五边形,
⊙O是五边形ABCD的外接圆.
证明:
AB=BC=CD=DE=EA,
︵
︵
︵
︵
︵
∵
∴ BCE=CDA=3AB,
︵
(2)五边形PQRST是⊙O的外切正五边形.
证明:连接OA、OB、OC,则OA=OB=OC,
∴∠OAB=∠OBA=∠OBC=∠OCB.
∵TP,PQ,QR分别是以点A、B、C为
切点的⊙O的切线.
∴∠OAP=∠OBP=∠OBQ=∠OCQ.
∴∠PAB=∠PBA=∠QBC=∠QCB.
A
B
C
D
E
O
P
Q
R
S
T
又∵AB=BC, ∴AB=BC.
∴△PAB≌△QBC.
∴∠P=∠Q,PQ=2PA.
同理可得∠Q=∠R=∠S=∠T,
QR=RS=ST=TP=2PA.
∵五边形PQRST的各边都与⊙O相切,
∴五边形PQRST是⊙O的外切正五边形.
A
B
C
D
E
O
P
Q
R
S
T
︵
︵
有关正多边形的作图
(1)用量角器等分圆周
已知⊙O的半径为2cm,求作圆的内接正三角形.
120°
A
O
C
B
用量角器度量,使∠AOB=
∠BOC=∠COA=120°.
正五角星的作法
72°
(2)用尺规等分圆周
用直尺和圆规作⊙O的两条互相垂直的直径,就可以把⊙O等分成4等份,从而作出正四边形.
正八边形的作法
在正四边形的基础上,我们再逐次平分各边所对的弧,就可以作出正八边形.
想一想:正十六边形怎么作?
正六边形的作法
设⊙O的半径为R,通常先作出⊙O的一条直径AB,然后分别以点A,B为圆心、R为半径作弧,与⊙O交于点C,D,E,F,从而得到⊙O的6等份点.
O
A
B
C
D
E
F
1.下列说法中正确的是( )
A.各边都相等的多边形是正多边形
B.正多边形既是轴对称图形,又是中心对称图形
C.各边都相等的圆内接多边形是正多边形
D.各角都相等的圆内接多边形是正多边形
C
随堂演练
2.如果一个正多边形的每个外角都等于36°,则这个多边形的中心角等于( )
A.36° B.18° C.72° D.54°
A
3.如图,点O是正六边形的对称中心,如果用一副三角板的角,借助点O(使直角的顶点落在点O处),把这个正六边形的面积n等分,那么n的所有可能取值的个数是( )
A.4 B.5 C.6 D.7
B
24.6 正多边形与圆
第2课时 正多边形的性质
沪科版数学九年级下册
第24章 圆
思 考
将一个圆n等分,就可以作出这个圆的内接或外切正n边形,反过来,是不是每个正多边形都有一个外接圆和一个内切圆呢?
我们仍然以五边形为例来进行研究.
如图,过正五边形ABCDE的顶点A,B,C作⊙O,连结OA,OB,OC,OD,OE.
∵ OB=OC,
∴ ∠OBC=∠OCB.
又 ∵ ∠ABC=∠BCD,
∴ ∠OBA=∠OCD.
A
B
C
D
E
O
新课推进
∵ AB=DC,
∴ △OAB≌△ODC.
∴ OA=OD,
即点D在⊙O上.
同理,得点E也在⊙O上.
所以正五边形ABCDE有一个以O为圆心的外接圆.
A
B
C
D
E
O
由于正五边形ABCDE的各边是⊙O中相等的弦,等弦的弦心距相等,所以以点O为圆心、弦心距OH为半径的圆与正五边形的各边都相切.
因而,正五边形ABCDE还有一个以O为圆心的内切圆.
A
B
C
D
E
O
H
任何正多边形都有一个外接圆和一个内切圆,并且这两个圆是同心圆.
正多边形的有关概念及相关计算
E
F
C
D
.
O
中心角
半径R
边心距r
正多边形的中心:该正多边形的外接圆和内切圆的公共圆心.
正多边形的半径:外接圆的半径.
正多边形的中心角:正多边形的每一条边所对的圆心角.
正多边形的边心距:内切圆的半径.
A
B
正n边形的一个内角的
度数是____________;
中心角是___________;
正多边形的中心角与外角的
大小关系是________.
中心角与内角互补.
相等
想一想:
E
D
C
B
A
O
F
正多边形都是轴对称图形,一个正n边形共有n条对称轴,每条对称轴都通过n边形的中心.
如果一个正多边形有偶数条边,那么它又是中心对称图形,它的中心就是对称中心.
例 求边长为a的正六边形的周长和面积.
解 如图,过正六边形的中心O作OG⊥BC,垂足是G,连接OB,OC,设该正六边形的周长和面积分别为C和S.
∵ 多边形ABCDEF是正六边形,
∴ ∠BOC=60°,△BOC是等边三角形.
∴ C=6BC=6a.
A
B
C
D
E
F
O
G
在△BOC中,有
A
B
C
D
E
F
O
G
1. 如图,要拧开一个边长为a=6mm的正六边形螺帽,扳手张开的开口b至少为多少?
随堂演练
解:如图,∠ABC=120°. AB=BC=a, AC=b.
过B作BD⊥AC于点D,
则AD=DC= b.
在Rt△ABD中,∠BAC=30°,
∴BD= AB=3mm.
∴b=2AD=6 mm.
即扳手张开的开口b至少要6 mm.
A
C
B D
2. 求出半径为R的圆内接正三角形的边长,边心距和面积.
解:作等边△ABC的BC边上的高AD,垂足为D
·
A
B
C
D
O
连接OB,则OB=R
在Rt△OBD中∠OBD=30°,
边心距=OD=
在Rt△ABD中∠BAD=30°,
·
A
B
C
D
O
谢谢观看
