25.2 三视图 课件(2课时、共43张PPT)2023-—2024学年沪科版数学九年级下册
文档属性
| 名称 | 25.2 三视图 课件(2课时、共43张PPT)2023-—2024学年沪科版数学九年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-27 16:17:35 | ||
图片预览







文档简介
(共43张PPT)
25.2 三视图
第1课时 三视图
沪科版数学九年级下册
第25章 投影与视图
新课导入
如果已知一个几何体在水平面上的视图是圆,你能断定这个几何体是球吗?
圆柱和球在水平面上的视图都是圆.
新课推进
要想清楚地刻画一个几何体的形状与大小,通常需要画出它在三个互相垂直的投影面上的正投影.
几何体正对着我们的面叫做正面,下方的面叫做水平面,右边的面叫做侧面.
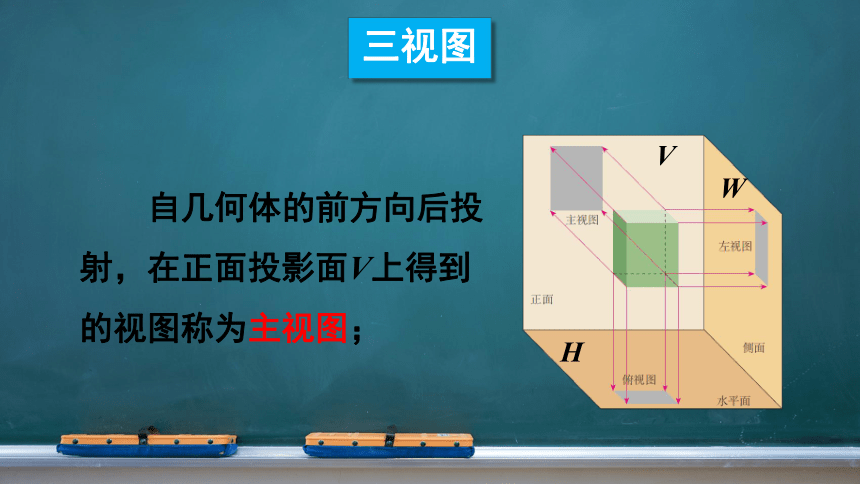
自几何体的前方向后投射,在正面投影面V上得到的视图称为主视图;
三视图
V
W
H
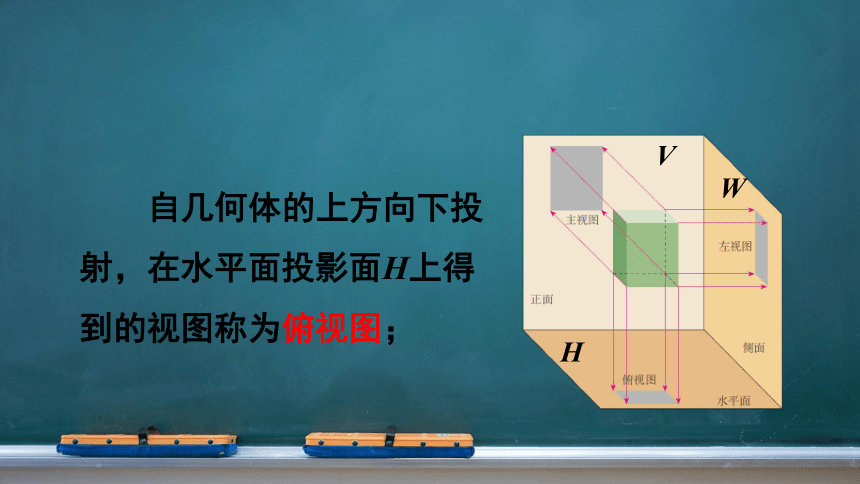
自几何体的上方向下投射,在水平面投影面H上得到的视图称为俯视图;
V
W
H
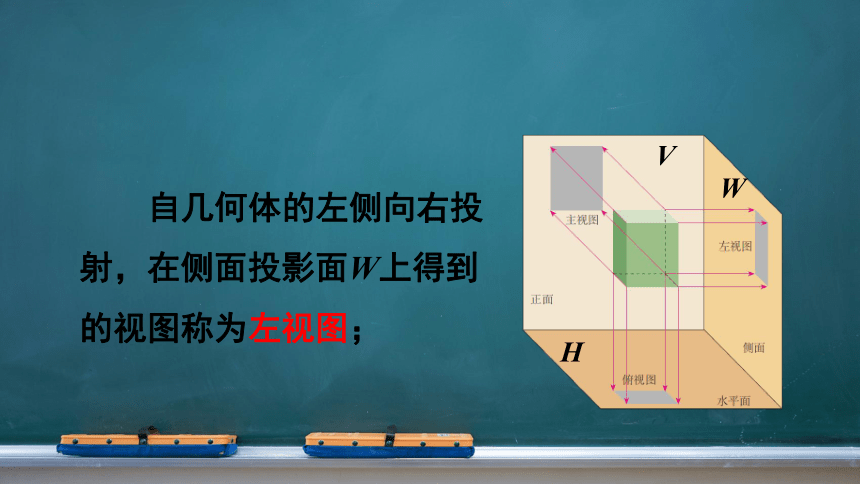
自几何体的左侧向右投射,在侧面投影面W上得到的视图称为左视图;
V
W
H
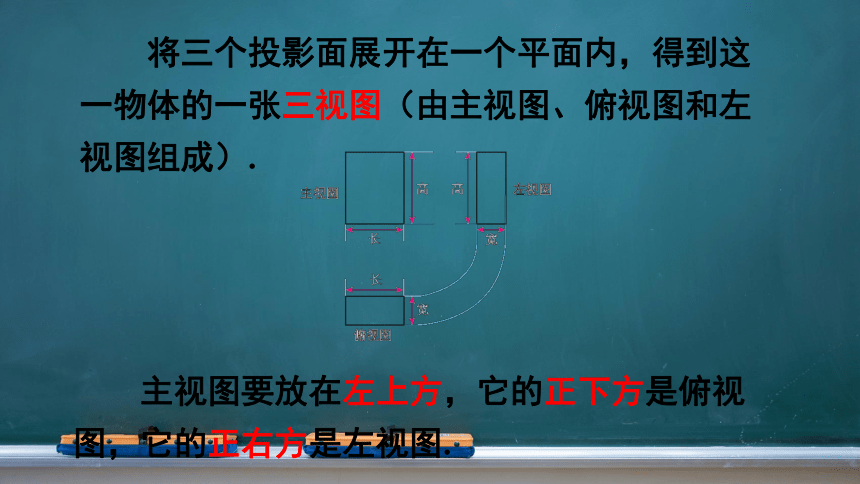
将三个投影面展开在一个平面内,得到这一物体的一张三视图(由主视图、俯视图和左视图组成).
主视图要放在左上方,它的正下方是俯视图,它的正右方是左视图.
长对正
高平齐
宽相等
主视图
左视图
俯视图
长
长
高
高
宽
宽
主视图与俯视图的长对正,主视图与左视图的高平齐,左视图与俯视图的宽相等.
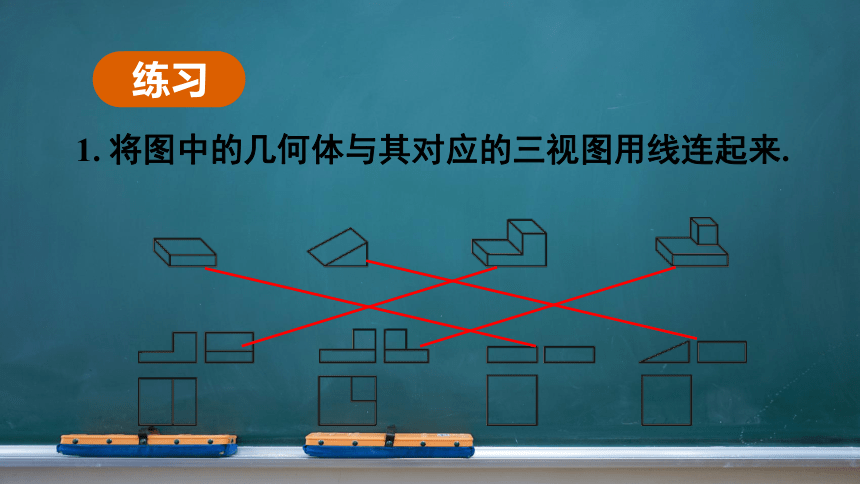
练习
1. 将图中的几何体与其对应的三视图用线连起来.
例1 画出图中几何体的三视图.
画三视图
画三视图的方法:
第一步,确定主视图的位置,画出主视图;
第二步,在主视图正下方画出俯视图,注意与主视图长对正;
第三步,在主视图正右方画出左视图,注意与主视图高平齐,与俯视图宽相等.
X
Y′
Y
Z
画三视图时,看得见部分的轮廓线画成实线,看不见部分的轮廓线画成虚线.
典例精析
例1 画出下列几何体的三视图.
主视图
俯视图
左视图
主视图
左视图
俯视图
主视图
俯视图
左视图
例2 画出如图所示的支架的三视图,其中支架的两个台阶的高度和宽度相等.
主视图
俯视图
左视图
随堂练习
1.下列几何体中,主视图、左视图和俯视图是全等形的几何体是( )
A.圆柱 B.正方体 C.棱柱 D.圆锥
B
2.某长方体的主视图和左视图如图所示(单位:cm),则其俯视图的面积是多少?
解 俯视图的长等于主视图的宽,为3cm
俯视图的宽等于左视图的宽,为2cm
则 其俯视图的面积为:3×2=6cm2
25.2 三视图
第2课时 视图的应用
沪科版数学九年级下册
第25章 投影与视图
新课导入
三棱柱
四棱柱
五棱柱
思 考
你能说说这个几何体的特点吗?
X
Y
Z
Y′
A′
B′
C′
A
B
C
像这样的几何体叫做棱柱,它的上下两个面叫做底面.(△ABC、△A′B′C′互相平行且是全等的三角形)
A′
B′
C′
A
B
C
其余各面叫做侧面,相邻侧面的交线叫做侧棱(各侧棱AA′,BB′,CC′平行且相等).
A′
B′
C′
A
B
C
当侧棱垂直于底面时,棱柱称为直棱柱,直棱柱的各个侧面都是矩形.
正三棱柱
正四棱柱
正六棱柱
底面是正多边形的直棱柱叫做正棱柱.
对于某些立体图形,沿着其中一些线(例如棱柱的棱)剪开,可以把立体图形的表面展开成一个平面图形,这个平面图形就是立体图形的展开图.
展开图
立体图
展开图
立体图
展开图
立体图
展开图
由展开图求面积
例2 某工厂要加工一批正六棱柱形状的食品盒,其三视图如图所示(单位:cm).问制作这样一个食品盒所需要硬纸板的面积至少为多少?(精确到1cm2)
X
Y
Z
Y′
10
36
解:这个正六棱柱形状的食品盒有六个侧面(都是矩形)和两个底面(都是正六边形),因此制作这样一个食品盒所需要的硬纸板的面积至少为
S = 6×10×36 + 2×6× ×102
= 2 160 +
≈ 2 680(cm2)
随堂演练
1.右图是一个多面体的表面展开图,那么这个多面体是( )
A.四棱柱 B.四棱锥
C.三棱柱 D.三棱锥
C
2.一个几何体的三视图如图所示,那么这个几何体的侧面积是( )
A. cm2 B. cm2
C. cm2 D. cm2
B
3.如图是一个包装盒的三视图,则这个包装盒的体积是( )
A. cm3
B. cm3
C. cm3
D. cm3
C
4. 画出下列三视图.
谢谢观看
25.2 三视图
第1课时 三视图
沪科版数学九年级下册
第25章 投影与视图
新课导入
如果已知一个几何体在水平面上的视图是圆,你能断定这个几何体是球吗?
圆柱和球在水平面上的视图都是圆.
新课推进
要想清楚地刻画一个几何体的形状与大小,通常需要画出它在三个互相垂直的投影面上的正投影.
几何体正对着我们的面叫做正面,下方的面叫做水平面,右边的面叫做侧面.
自几何体的前方向后投射,在正面投影面V上得到的视图称为主视图;
三视图
V
W
H
自几何体的上方向下投射,在水平面投影面H上得到的视图称为俯视图;
V
W
H
自几何体的左侧向右投射,在侧面投影面W上得到的视图称为左视图;
V
W
H
将三个投影面展开在一个平面内,得到这一物体的一张三视图(由主视图、俯视图和左视图组成).
主视图要放在左上方,它的正下方是俯视图,它的正右方是左视图.
长对正
高平齐
宽相等
主视图
左视图
俯视图
长
长
高
高
宽
宽
主视图与俯视图的长对正,主视图与左视图的高平齐,左视图与俯视图的宽相等.
练习
1. 将图中的几何体与其对应的三视图用线连起来.
例1 画出图中几何体的三视图.
画三视图
画三视图的方法:
第一步,确定主视图的位置,画出主视图;
第二步,在主视图正下方画出俯视图,注意与主视图长对正;
第三步,在主视图正右方画出左视图,注意与主视图高平齐,与俯视图宽相等.
X
Y′
Y
Z
画三视图时,看得见部分的轮廓线画成实线,看不见部分的轮廓线画成虚线.
典例精析
例1 画出下列几何体的三视图.
主视图
俯视图
左视图
主视图
左视图
俯视图
主视图
俯视图
左视图
例2 画出如图所示的支架的三视图,其中支架的两个台阶的高度和宽度相等.
主视图
俯视图
左视图
随堂练习
1.下列几何体中,主视图、左视图和俯视图是全等形的几何体是( )
A.圆柱 B.正方体 C.棱柱 D.圆锥
B
2.某长方体的主视图和左视图如图所示(单位:cm),则其俯视图的面积是多少?
解 俯视图的长等于主视图的宽,为3cm
俯视图的宽等于左视图的宽,为2cm
则 其俯视图的面积为:3×2=6cm2
25.2 三视图
第2课时 视图的应用
沪科版数学九年级下册
第25章 投影与视图
新课导入
三棱柱
四棱柱
五棱柱
思 考
你能说说这个几何体的特点吗?
X
Y
Z
Y′
A′
B′
C′
A
B
C
像这样的几何体叫做棱柱,它的上下两个面叫做底面.(△ABC、△A′B′C′互相平行且是全等的三角形)
A′
B′
C′
A
B
C
其余各面叫做侧面,相邻侧面的交线叫做侧棱(各侧棱AA′,BB′,CC′平行且相等).
A′
B′
C′
A
B
C
当侧棱垂直于底面时,棱柱称为直棱柱,直棱柱的各个侧面都是矩形.
正三棱柱
正四棱柱
正六棱柱
底面是正多边形的直棱柱叫做正棱柱.
对于某些立体图形,沿着其中一些线(例如棱柱的棱)剪开,可以把立体图形的表面展开成一个平面图形,这个平面图形就是立体图形的展开图.
展开图
立体图
展开图
立体图
展开图
立体图
展开图
由展开图求面积
例2 某工厂要加工一批正六棱柱形状的食品盒,其三视图如图所示(单位:cm).问制作这样一个食品盒所需要硬纸板的面积至少为多少?(精确到1cm2)
X
Y
Z
Y′
10
36
解:这个正六棱柱形状的食品盒有六个侧面(都是矩形)和两个底面(都是正六边形),因此制作这样一个食品盒所需要的硬纸板的面积至少为
S = 6×10×36 + 2×6× ×102
= 2 160 +
≈ 2 680(cm2)
随堂演练
1.右图是一个多面体的表面展开图,那么这个多面体是( )
A.四棱柱 B.四棱锥
C.三棱柱 D.三棱锥
C
2.一个几何体的三视图如图所示,那么这个几何体的侧面积是( )
A. cm2 B. cm2
C. cm2 D. cm2
B
3.如图是一个包装盒的三视图,则这个包装盒的体积是( )
A. cm3
B. cm3
C. cm3
D. cm3
C
4. 画出下列三视图.
谢谢观看
