24.1旋转 课件(3课时、共77张PPT)2023-2024学年 沪科版数学九年级下册
文档属性
| 名称 | 24.1旋转 课件(3课时、共77张PPT)2023-2024学年 沪科版数学九年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 8.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-27 00:00:00 | ||
图片预览






文档简介
(共77张PPT)
24.1 旋转
第1课时 旋转、旋转对称图形
沪科版数学九年级下册
第24章 圆
新课导入
思 考:
这些运动有什么共同的特征?
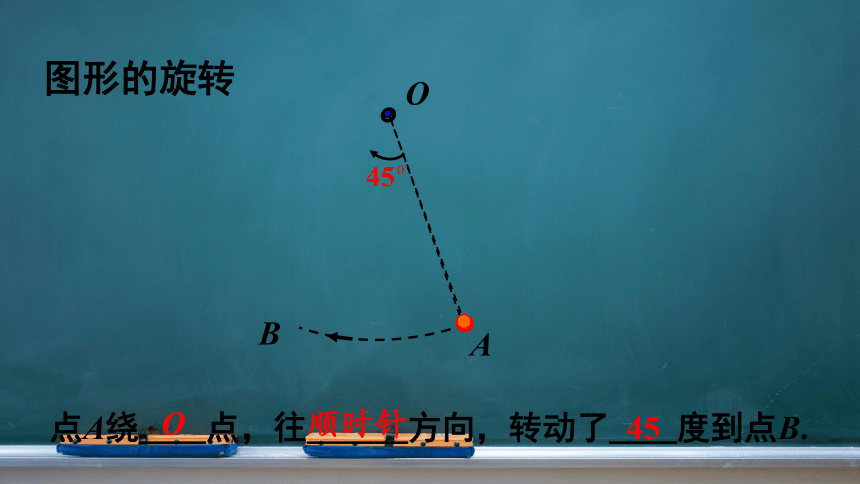
图形的旋转
B
O
A
45
0
点A绕__点,往___方向,转动了__度到点B.
O
顺时针
45
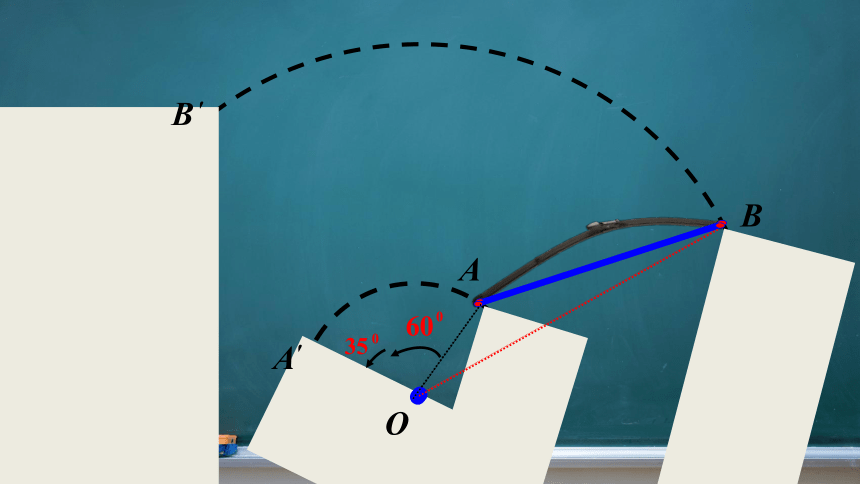
O
B
A
B
′
A
′
60
0
35
0
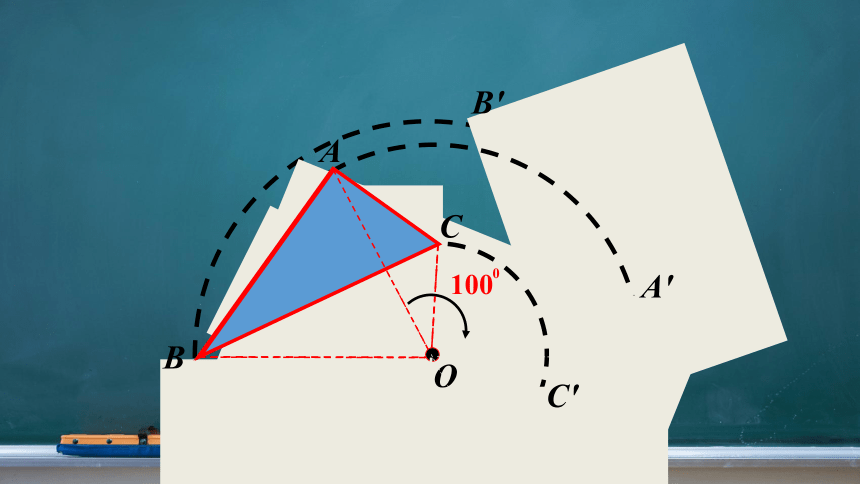
B
A
B′
A′
O
C
100
0
C′
推进新课
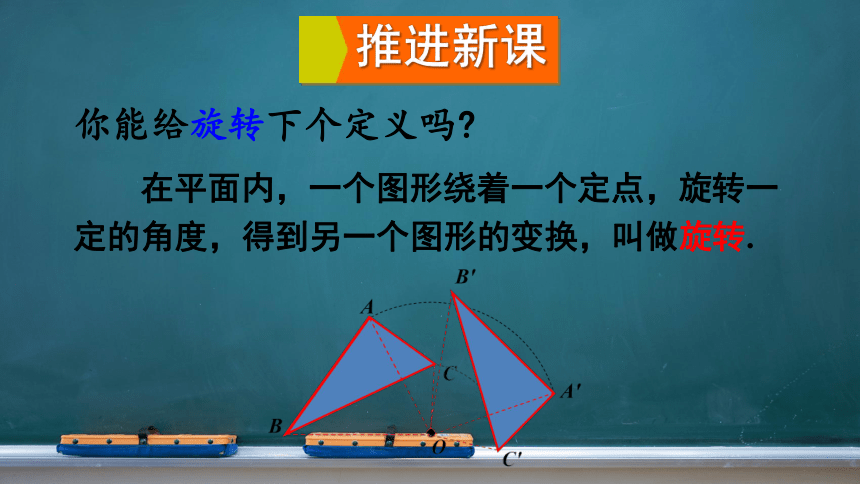
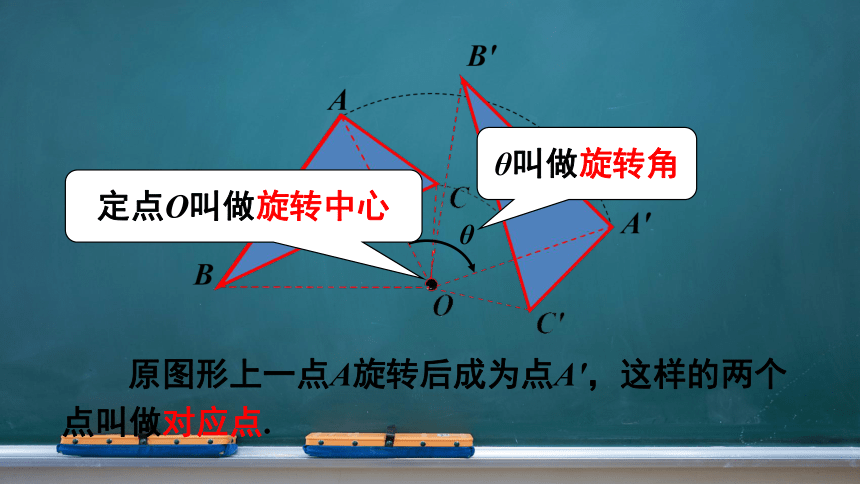
在平面内,一个图形绕着一个定点,旋转一定的角度,得到另一个图形的变换,叫做旋转.
你能给旋转下个定义吗
θ
原图形上一点A旋转后成为点A′,这样的两个点叫做对应点.
定点O叫做旋转中心
θ叫做旋转角
从课本中的思考实例可以看出:图形的旋转三要素是 , , .
旋转中心
旋转方向
旋转角
试一试
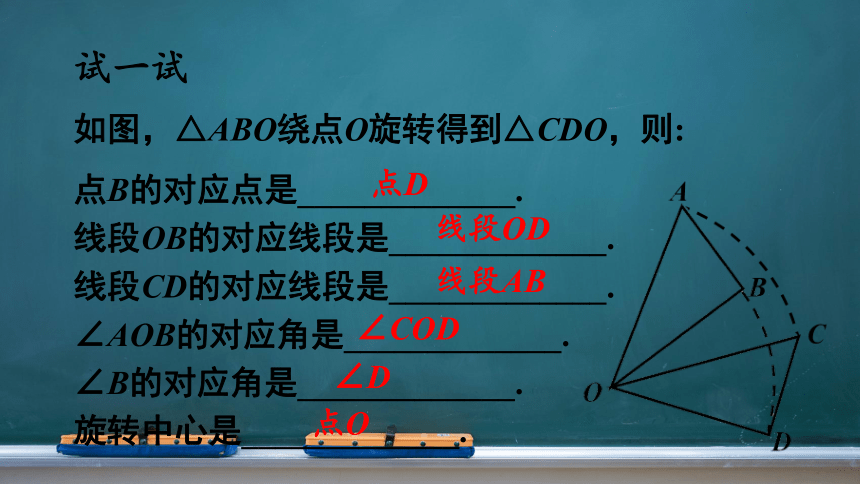
如图,△ABO绕点O旋转得到△CDO,则:
点B的对应点是_____________.
线段OB的对应线段是_____________.
线段CD的对应线段是_____________.
∠AOB的对应角是_____________.
∠B的对应角是_____________.
旋转中心是_____________.
点D
线段OD
线段AB
∠COD
∠D
点O
旋转中心就是在旋转过程中始终保持固定不变的那个点,它可以在图形的外部或内部,还可以在图形上,即它可以是平面内的任意一点.
旋转角:任意一对对应点与旋转中心的连线所成的角.
①时钟的时针在不停地旋转,从上午6时到上午9时,时针旋转的角度是多少?从上午9时到上午10时呢?
解:从上午6时到上午9时,时针旋转的角度为90°,从上午9时到上午10时,时针旋转的角度是30°.
练习
②如图,杠杆绕支点转动撬起重物,杠杆的旋转中心是点 ,旋转角是 ,点A的对应点是点 .
O
∠AOA′
A′
观察
如图,△ABC绕着旋转中心O按逆时针方向旋转θ后,得到△A′B′C′.
①OA与OA′、OB与OB′、OC与OC′分别有何关系? .
②∠AOA′、∠BOB′、∠COC′之间有何关系? .
③△ABC与△A′B′C′有何关系?
.
分别相等
∠AOA′=∠BOB′=∠COC′
△ABC≌△A′B′C′
在一个图形和它经过旋转所得到的图形中,对应点到旋转中心的距离相等;两组对应点分别与旋转中心的连线所成的角相等,都等于旋转角;旋转中心是唯一不动的点.
归纳小结
◆旋转前、后的图形全等.
◆对应点到旋转中心的距离相等.
◆每一对对应点与旋转中心的连线所成的角彼此相等.
◆图形的旋转是由旋转中心和旋转的角度决定.
旋转的基本性质
思 考:
这些图形有什么共同特征?
在平面内,一个图形绕着一个定点旋转一定的角度θ(0°<θ<360°)后,能够与原图形重合,这样的图形叫做旋转对称图形.
B
A
C
O
一个图形绕着一个定点,按照一定的角度,从一个位置旋转到另一个位置,叫做旋转.
A
B
C
O
·
一个图形绕着一个定点,旋转一定的角度后能与自身重合,这样的图形称为旋转对称图形.
图形的一种变换
图形的一种特性
思考:香港特别行政区区徽可以看作是什么“基本图案”通过怎样的旋转而得到的?
可以看作是一个花瓣连续4次旋转所形成的,每次旋转分别等于72°
随堂练习
1. 下列现象中属于旋转的有( )
①火车行驶;②荡秋千运动;③方向盘的转动;④钟摆的运动;⑤圆规画圆.
A.1个 B.2个 C.3个 D.4个
D
2. 把图中的五角星图案,绕着它的中心点O旋转,旋转角为多少度时,旋转后的五角星能与自身重合?
解:旋转角为72°或144°或216°或288°时,
旋转后的五角星能与自身重合.
3. 如图,△ABD、△AEC都是等边三角形,BE与DC有什么关系?你能用旋转的性质说明上述关系成立的理由吗?
解:BE=DC.
理由:将△ABE顺时针绕点A顺时针旋转60°就能和△ACD重合. 即△ADC≌△ABE,所以BE=DC.
旋转前后两个图形的形状、大小不变,因此我们在用旋转解决与其相关的问题时要注意:
①明确旋转中的“变”与“不变”;
②明确旋转前后的对应关系;
③明确旋转过程中线段或角之间的关系.
课堂小结
24.1 旋转
第2课时 中心对称与中心对称图形
沪科版数学九年级下册
第24章 圆
新课导入
问题1:把图中三角形绕定点O旋转180°,你有什么发现?
A
B
C
O
180°
问题2:如图,线段AC、BD相交于点O,OA=OC,OB=OD.把△OCD绕点O旋转180°,你又有什么发现?
推进新课
你发现了什么?
把一个图形 ,如果它 ,那么就说这两个图形关于这个点 或 ,这个点叫做 . 这两个图形在旋转后能重合的对应点叫做关于对称中心的对称点.
绕着某一点旋转180°
能够与另一个图形重合
对称
中心对称
对称中心(简称中心)
A
B
C
O
180°
A′
B′
C′
找一找:下图中△A′B′C′与△ABC关于点O是成中心对称的,你能从图中找到哪些等量关系
思考:观察上图,两个图形形成中心对称,说一说中心对称有什么特性?
1.关于中心对称的两个图形,对称点所连线段都经过对称中心,并且被对称中心所平分.
2.关于中心对称的两个图形是全等形.
归纳:中心对称的性质
想一想:中心对称与轴对称有什么区别 又有什么联系
轴对称 中心对称
有一条对称轴---直线 有一个对称中心—点
图形沿对称轴对折(翻折180°)后重合 图形绕对称中心旋转180°后重合
对称点的连线被对称轴垂直平分 对称点连线经过对称中心,且被对称中心平分
思考1:已知A点和O点,你能画出点A关于点O的对称点A'吗?
A
O
A'
连结OA,
并延长到A',使OA'=OA,
则A'是所求的点
思考2:已知线段AB和O点,画出线段AB关于点O的对称线段A' B' .
O
A
B
连结AO并延长到A',使OA'=OA,则得A的对称点A'
A'
连结BO并延长到B' ,使OB' =OB,则得B的对称点B'
B'
连结 A'B' ,则线段A'B'是所画线段
例 如图,已知四边形ABCD和点O,试画出四边形ABCD关于点O成中心对称的图形A'B'C'D'.
A
B
C
D
O
怎么办?
A
B
C
D
O
分析:要画出四边形ABCD关于点O成中心对称的图形,只要画出A,B,C,D四点关于点O的对应点,再顺次连接各对应点即可.
A
B
C
D
O
1.连结AO并延长到A',使OA'=OA,得到点A的对应点A'
A′
2.同理,可作出点B,C,D的对应点B',C',D'.
B′
C′
D′
3.顺次连接点A',B',C',D'.则四边形A'B'C'D'即为所作.
想一想:如图,已知△ABC与△A′B′C′中心对称,怎样求出它们的对称中心O?
A
B
C
A’
B’
C’
观察:将下面的图形绕O点旋转180°,你有什么发现?
A
B
O
O
O
O
O
B
A
C
D
如果一个图形绕一个点旋转180°后,能和原来的图形互相重合,那么这个图形叫做中心对称图形;这个点叫做它的对称中心;互相重合的点叫做对称点.
下面哪些图形是中心对称图形
问题:我们平时见过的几何图形中,有哪些是中心对称图形?并指出对称中心.
比较中心对称和中心对称图形的概念,试说明它们有何区别与联系.
区别:中心对称是针对两个图形而言的,而中心对称图形是针对单个图形而言的.
联系:如果把成中心对称的两个图形看成一个整体,则该图形为中心对称图形;如果把一个中心对称图形相互对称的两部分看成两个图形,则它们成中心对称.
中心对称图形
随堂练习
1.下列图形中既是轴对称图形又是中心对称图形的是( )
A.角 B.等边三角形 C.线段 D.平行四边形
2.下列多边形中,是中心对称图形而不是轴对称图形的是( )
A.平行四边形 B.矩形 C.菱形 D.正方形
C
A
3.下列标志中,可以看做是中心对称图形的是( )
D
4. 如图,△ABC与△A1B1C1关于点O成中心对称,下列说法:①∠BAC=∠B1A1C1;②AC=A1C1; ③OA=OA1;④△ABC与△A1B1C1的面积相等.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
D
o
5. 如图,在△ABC中,AB=AC,若将△ABC绕点C顺时针旋转180°得到△FEC.
(1)试猜想AE与BF有何关系?说明理由;
(2)若△ABC的面积为3cm2,求四边形ABFE的面积.
解:(1)AE∥BF,AE=BF;
理由:∵△ABC绕点C顺时针旋转180°得到△FEC,
∴△ABC≌△FEC,
∴AB=FE,∠ABC=∠FEC,
∴AB∥FE,
∴四边形ABFE为平行四边形,AE∥BF,AE=BF .
(2)S四边形ABFE=4S△ABC=12 cm2.
课堂小结
中心对称是针对两个图形而言的,中心对称图形是针对一个图形而言的.
把一个图形绕着某一个点旋转180°后,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形.
24.1 旋转
第3课时 在平面直角坐标系中对图形进行旋转变换
沪科版数学九年级下册
第24章 圆
复习导入
旋转的定义:
在平面内,将一个图形绕着一个定点沿某个方向转动一个角度,得到另一个图形的变换,这样的图形变换称为旋转。
中心对称的定义:
在平面内,将一个图形绕着某一定点旋转180度,得到另一个图形,那么,我们就说这两个图形关于这个点成中心对称。
旋转的性质:
1. 旋转不改变图形的大小和形状.
2. 任意一对对应点与旋转中心的连线所成的角相等,都等于旋转角.
3. 对应点到旋转中心的距离相等.
4. 旋转中心是唯一不动的点.
中心对称的性质:
关于中心对称的两个图形,对应点所连线段都经过对称中心,并且被对称中心所平分,具有旋转的所有性质.
旋转对称图形:
在平面内,一个图形绕着一个定点旋转一定的角度后,能够与原图_______,这样的图形叫做旋转对称图形,这个定点就是_________.
重合
旋转中心
中心对称图形定义:
如果一个图形绕一个点旋转180°后,能和原来的图形互相重合,那么这个图形叫做中心对称图形;这个点叫做它的对称中心.
推进新课
如图,△ABC的顶点坐标分别是A(2,1),B(0,0),C(2,0).
x
y
O
1
2
-2
-1
1
2
-2
-1
A
B
C
(1)分别画出△ABC以点O(0,0)为旋转中心,在图(1)中旋转90°、在图(2)中旋转180°、在图(3)中旋转270°、在图(4)中旋转360°而得到的△A′B′C′;
x
y
O
1
2
-2
-1
1
2
-2
-1
A
B
C
A′
C′
B′
x
y
O
1
2
-2
-1
1
2
-2
-1
A
B
C
A′
C′
B′
(1)
(2)
x
y
O
1
2
-2
-1
1
2
-2
-1
A
B
C
A′
C′
B′
(3)
x
y
O
1
2
-2
-1
1
2
-2
-1
A
B
C
A′
C′
B′
(4)
(2)给出点A′,B′,C′的坐标(填在下表中):
原图形上点的坐标 A(2,1) B(0,0) C(2,0)
按逆时针方向旋转后对应点坐标 以点O为旋转中心旋转90°
以点O为旋转中心旋转180°
以点O为旋转中心旋转270°
以点O为旋转中心旋转360°
A′(-1,2)
B′(0,0)
C′(0,2)
A′(-2,-1)
B′(0,0)
C′(-2,0)
A′(1,-2)
B′(0,0)
C′(0,-2)
A′(2,1)
B′(0,0)
C′(2,0)
思考:分别比较点A′与点A、点B′与点B、点C′与点C的坐标,能得到怎样的结论?
通过作图、分析能看到,把一个图形以点O为旋转中心作几个特殊角度的旋转,可得如下结果:
原图形上任意一点坐标 以点O为旋转中心按逆时针方向旋转后对应点坐标 旋转90° 旋转180° 旋转270° 旋转360°
(x,y)
(-y,x)
(-x,-y)
(y,-x)
(x,y)
这里,把(x,y)变换成(x,y)的变换叫做恒等变换,即在平面直角坐标系中,一个图形绕点O作360°旋转是一个恒等变换.
x
y
O
1
2
-2
-1
1
2
-2
-1
A
B
C
A′
C′
B′
应用巩固
已知点A的坐标为(-2,1),将点A绕着原点逆时针旋转90°,则点A的对应点A1的坐标是(___________);绕着原点逆时针旋转180°,则点A的对应点A2的坐标是(___________);绕着原点逆时针旋转270°,则点A的对应点A3的坐标是(__________);绕着原点逆时针旋转360°,则点A的对应点A4的坐标是(__________).
-1,-2
2,-1
1,2
-2,1
已知如图,△ABC与△DEF关于原点O成中心对称,A(-1,2),C(-1,1),E(4,-3),则B、D、F的坐标分别为B(_____),D(_____),F(_____).
-4,3
1,-2
1,-1
随堂练习
1.如图,将线段AB绕点O顺时针旋转90°得到线段A′B′,那么A(-2,5)的对应点A′的坐标是( )
A.(2,5)
B.(5,2)
C.(2,-5)
D.(5,-2)
B
2.已知:如图,E(-4,2),F(-1,-1),以O为中心,把△EFO旋转180°,则点E的对应点E′的坐标为(_____________).
4,-2
3.如图是某设计师在方格纸中设计图案的一部分,请你帮他完成余下的工作:
(1)作出关于AB所在直线的轴对称图形;
(2)将你画出的部分连同原图形绕点O逆时针旋转90°;
(3)发挥你的想象,给得到的图案适当涂上阴影,让它变得更加美丽.
[解析] (1)根据轴对称的概念先找到图形上的关键点关于AB所在直线的对称点,然后顺次连接起来即可;(2)将图形的各个顶点绕旋转中心O逆时针旋转90°后的对应点描出来,然后顺次连接起来即可;(3)根据自己的想象恰当地涂色.
解:如图:
[归纳] 利用平移、轴对称、旋转等变换设计图案,一般都是先找“关键点”,再作关键点的对应点,然后顺次连接起来即可.
平移
轴对称
旋转
图形变换的基本方式有哪些?
思考:我们可以将这些图形变换的方式组合起来吗?
知识拓展
你能利用上述方式设计出美丽的图案吗?
课堂小结
1.在平面直角坐标系中,以原点为旋转中心把一个图形按逆时针方向旋转,原图上任意一点坐标(x,y)旋转特定角度后对应点的坐标如下表:
旋转角度 90° 180° 270° 360°
对应点坐标(x,y) ________ ________ ________ ________
(-y,x)
(-x,-y)
(y,-x)
(x,y)
2.把(x,y)变换成__________的变换叫做恒等变换.
(x,y)
谢谢观看
24.1 旋转
第1课时 旋转、旋转对称图形
沪科版数学九年级下册
第24章 圆
新课导入
思 考:
这些运动有什么共同的特征?
图形的旋转
B
O
A
45
0
点A绕__点,往___方向,转动了__度到点B.
O
顺时针
45
O
B
A
B
′
A
′
60
0
35
0
B
A
B′
A′
O
C
100
0
C′
推进新课
在平面内,一个图形绕着一个定点,旋转一定的角度,得到另一个图形的变换,叫做旋转.
你能给旋转下个定义吗
θ
原图形上一点A旋转后成为点A′,这样的两个点叫做对应点.
定点O叫做旋转中心
θ叫做旋转角
从课本中的思考实例可以看出:图形的旋转三要素是 , , .
旋转中心
旋转方向
旋转角
试一试
如图,△ABO绕点O旋转得到△CDO,则:
点B的对应点是_____________.
线段OB的对应线段是_____________.
线段CD的对应线段是_____________.
∠AOB的对应角是_____________.
∠B的对应角是_____________.
旋转中心是_____________.
点D
线段OD
线段AB
∠COD
∠D
点O
旋转中心就是在旋转过程中始终保持固定不变的那个点,它可以在图形的外部或内部,还可以在图形上,即它可以是平面内的任意一点.
旋转角:任意一对对应点与旋转中心的连线所成的角.
①时钟的时针在不停地旋转,从上午6时到上午9时,时针旋转的角度是多少?从上午9时到上午10时呢?
解:从上午6时到上午9时,时针旋转的角度为90°,从上午9时到上午10时,时针旋转的角度是30°.
练习
②如图,杠杆绕支点转动撬起重物,杠杆的旋转中心是点 ,旋转角是 ,点A的对应点是点 .
O
∠AOA′
A′
观察
如图,△ABC绕着旋转中心O按逆时针方向旋转θ后,得到△A′B′C′.
①OA与OA′、OB与OB′、OC与OC′分别有何关系? .
②∠AOA′、∠BOB′、∠COC′之间有何关系? .
③△ABC与△A′B′C′有何关系?
.
分别相等
∠AOA′=∠BOB′=∠COC′
△ABC≌△A′B′C′
在一个图形和它经过旋转所得到的图形中,对应点到旋转中心的距离相等;两组对应点分别与旋转中心的连线所成的角相等,都等于旋转角;旋转中心是唯一不动的点.
归纳小结
◆旋转前、后的图形全等.
◆对应点到旋转中心的距离相等.
◆每一对对应点与旋转中心的连线所成的角彼此相等.
◆图形的旋转是由旋转中心和旋转的角度决定.
旋转的基本性质
思 考:
这些图形有什么共同特征?
在平面内,一个图形绕着一个定点旋转一定的角度θ(0°<θ<360°)后,能够与原图形重合,这样的图形叫做旋转对称图形.
B
A
C
O
一个图形绕着一个定点,按照一定的角度,从一个位置旋转到另一个位置,叫做旋转.
A
B
C
O
·
一个图形绕着一个定点,旋转一定的角度后能与自身重合,这样的图形称为旋转对称图形.
图形的一种变换
图形的一种特性
思考:香港特别行政区区徽可以看作是什么“基本图案”通过怎样的旋转而得到的?
可以看作是一个花瓣连续4次旋转所形成的,每次旋转分别等于72°
随堂练习
1. 下列现象中属于旋转的有( )
①火车行驶;②荡秋千运动;③方向盘的转动;④钟摆的运动;⑤圆规画圆.
A.1个 B.2个 C.3个 D.4个
D
2. 把图中的五角星图案,绕着它的中心点O旋转,旋转角为多少度时,旋转后的五角星能与自身重合?
解:旋转角为72°或144°或216°或288°时,
旋转后的五角星能与自身重合.
3. 如图,△ABD、△AEC都是等边三角形,BE与DC有什么关系?你能用旋转的性质说明上述关系成立的理由吗?
解:BE=DC.
理由:将△ABE顺时针绕点A顺时针旋转60°就能和△ACD重合. 即△ADC≌△ABE,所以BE=DC.
旋转前后两个图形的形状、大小不变,因此我们在用旋转解决与其相关的问题时要注意:
①明确旋转中的“变”与“不变”;
②明确旋转前后的对应关系;
③明确旋转过程中线段或角之间的关系.
课堂小结
24.1 旋转
第2课时 中心对称与中心对称图形
沪科版数学九年级下册
第24章 圆
新课导入
问题1:把图中三角形绕定点O旋转180°,你有什么发现?
A
B
C
O
180°
问题2:如图,线段AC、BD相交于点O,OA=OC,OB=OD.把△OCD绕点O旋转180°,你又有什么发现?
推进新课
你发现了什么?
把一个图形 ,如果它 ,那么就说这两个图形关于这个点 或 ,这个点叫做 . 这两个图形在旋转后能重合的对应点叫做关于对称中心的对称点.
绕着某一点旋转180°
能够与另一个图形重合
对称
中心对称
对称中心(简称中心)
A
B
C
O
180°
A′
B′
C′
找一找:下图中△A′B′C′与△ABC关于点O是成中心对称的,你能从图中找到哪些等量关系
思考:观察上图,两个图形形成中心对称,说一说中心对称有什么特性?
1.关于中心对称的两个图形,对称点所连线段都经过对称中心,并且被对称中心所平分.
2.关于中心对称的两个图形是全等形.
归纳:中心对称的性质
想一想:中心对称与轴对称有什么区别 又有什么联系
轴对称 中心对称
有一条对称轴---直线 有一个对称中心—点
图形沿对称轴对折(翻折180°)后重合 图形绕对称中心旋转180°后重合
对称点的连线被对称轴垂直平分 对称点连线经过对称中心,且被对称中心平分
思考1:已知A点和O点,你能画出点A关于点O的对称点A'吗?
A
O
A'
连结OA,
并延长到A',使OA'=OA,
则A'是所求的点
思考2:已知线段AB和O点,画出线段AB关于点O的对称线段A' B' .
O
A
B
连结AO并延长到A',使OA'=OA,则得A的对称点A'
A'
连结BO并延长到B' ,使OB' =OB,则得B的对称点B'
B'
连结 A'B' ,则线段A'B'是所画线段
例 如图,已知四边形ABCD和点O,试画出四边形ABCD关于点O成中心对称的图形A'B'C'D'.
A
B
C
D
O
怎么办?
A
B
C
D
O
分析:要画出四边形ABCD关于点O成中心对称的图形,只要画出A,B,C,D四点关于点O的对应点,再顺次连接各对应点即可.
A
B
C
D
O
1.连结AO并延长到A',使OA'=OA,得到点A的对应点A'
A′
2.同理,可作出点B,C,D的对应点B',C',D'.
B′
C′
D′
3.顺次连接点A',B',C',D'.则四边形A'B'C'D'即为所作.
想一想:如图,已知△ABC与△A′B′C′中心对称,怎样求出它们的对称中心O?
A
B
C
A’
B’
C’
观察:将下面的图形绕O点旋转180°,你有什么发现?
A
B
O
O
O
O
O
B
A
C
D
如果一个图形绕一个点旋转180°后,能和原来的图形互相重合,那么这个图形叫做中心对称图形;这个点叫做它的对称中心;互相重合的点叫做对称点.
下面哪些图形是中心对称图形
问题:我们平时见过的几何图形中,有哪些是中心对称图形?并指出对称中心.
比较中心对称和中心对称图形的概念,试说明它们有何区别与联系.
区别:中心对称是针对两个图形而言的,而中心对称图形是针对单个图形而言的.
联系:如果把成中心对称的两个图形看成一个整体,则该图形为中心对称图形;如果把一个中心对称图形相互对称的两部分看成两个图形,则它们成中心对称.
中心对称图形
随堂练习
1.下列图形中既是轴对称图形又是中心对称图形的是( )
A.角 B.等边三角形 C.线段 D.平行四边形
2.下列多边形中,是中心对称图形而不是轴对称图形的是( )
A.平行四边形 B.矩形 C.菱形 D.正方形
C
A
3.下列标志中,可以看做是中心对称图形的是( )
D
4. 如图,△ABC与△A1B1C1关于点O成中心对称,下列说法:①∠BAC=∠B1A1C1;②AC=A1C1; ③OA=OA1;④△ABC与△A1B1C1的面积相等.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
D
o
5. 如图,在△ABC中,AB=AC,若将△ABC绕点C顺时针旋转180°得到△FEC.
(1)试猜想AE与BF有何关系?说明理由;
(2)若△ABC的面积为3cm2,求四边形ABFE的面积.
解:(1)AE∥BF,AE=BF;
理由:∵△ABC绕点C顺时针旋转180°得到△FEC,
∴△ABC≌△FEC,
∴AB=FE,∠ABC=∠FEC,
∴AB∥FE,
∴四边形ABFE为平行四边形,AE∥BF,AE=BF .
(2)S四边形ABFE=4S△ABC=12 cm2.
课堂小结
中心对称是针对两个图形而言的,中心对称图形是针对一个图形而言的.
把一个图形绕着某一个点旋转180°后,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形.
24.1 旋转
第3课时 在平面直角坐标系中对图形进行旋转变换
沪科版数学九年级下册
第24章 圆
复习导入
旋转的定义:
在平面内,将一个图形绕着一个定点沿某个方向转动一个角度,得到另一个图形的变换,这样的图形变换称为旋转。
中心对称的定义:
在平面内,将一个图形绕着某一定点旋转180度,得到另一个图形,那么,我们就说这两个图形关于这个点成中心对称。
旋转的性质:
1. 旋转不改变图形的大小和形状.
2. 任意一对对应点与旋转中心的连线所成的角相等,都等于旋转角.
3. 对应点到旋转中心的距离相等.
4. 旋转中心是唯一不动的点.
中心对称的性质:
关于中心对称的两个图形,对应点所连线段都经过对称中心,并且被对称中心所平分,具有旋转的所有性质.
旋转对称图形:
在平面内,一个图形绕着一个定点旋转一定的角度后,能够与原图_______,这样的图形叫做旋转对称图形,这个定点就是_________.
重合
旋转中心
中心对称图形定义:
如果一个图形绕一个点旋转180°后,能和原来的图形互相重合,那么这个图形叫做中心对称图形;这个点叫做它的对称中心.
推进新课
如图,△ABC的顶点坐标分别是A(2,1),B(0,0),C(2,0).
x
y
O
1
2
-2
-1
1
2
-2
-1
A
B
C
(1)分别画出△ABC以点O(0,0)为旋转中心,在图(1)中旋转90°、在图(2)中旋转180°、在图(3)中旋转270°、在图(4)中旋转360°而得到的△A′B′C′;
x
y
O
1
2
-2
-1
1
2
-2
-1
A
B
C
A′
C′
B′
x
y
O
1
2
-2
-1
1
2
-2
-1
A
B
C
A′
C′
B′
(1)
(2)
x
y
O
1
2
-2
-1
1
2
-2
-1
A
B
C
A′
C′
B′
(3)
x
y
O
1
2
-2
-1
1
2
-2
-1
A
B
C
A′
C′
B′
(4)
(2)给出点A′,B′,C′的坐标(填在下表中):
原图形上点的坐标 A(2,1) B(0,0) C(2,0)
按逆时针方向旋转后对应点坐标 以点O为旋转中心旋转90°
以点O为旋转中心旋转180°
以点O为旋转中心旋转270°
以点O为旋转中心旋转360°
A′(-1,2)
B′(0,0)
C′(0,2)
A′(-2,-1)
B′(0,0)
C′(-2,0)
A′(1,-2)
B′(0,0)
C′(0,-2)
A′(2,1)
B′(0,0)
C′(2,0)
思考:分别比较点A′与点A、点B′与点B、点C′与点C的坐标,能得到怎样的结论?
通过作图、分析能看到,把一个图形以点O为旋转中心作几个特殊角度的旋转,可得如下结果:
原图形上任意一点坐标 以点O为旋转中心按逆时针方向旋转后对应点坐标 旋转90° 旋转180° 旋转270° 旋转360°
(x,y)
(-y,x)
(-x,-y)
(y,-x)
(x,y)
这里,把(x,y)变换成(x,y)的变换叫做恒等变换,即在平面直角坐标系中,一个图形绕点O作360°旋转是一个恒等变换.
x
y
O
1
2
-2
-1
1
2
-2
-1
A
B
C
A′
C′
B′
应用巩固
已知点A的坐标为(-2,1),将点A绕着原点逆时针旋转90°,则点A的对应点A1的坐标是(___________);绕着原点逆时针旋转180°,则点A的对应点A2的坐标是(___________);绕着原点逆时针旋转270°,则点A的对应点A3的坐标是(__________);绕着原点逆时针旋转360°,则点A的对应点A4的坐标是(__________).
-1,-2
2,-1
1,2
-2,1
已知如图,△ABC与△DEF关于原点O成中心对称,A(-1,2),C(-1,1),E(4,-3),则B、D、F的坐标分别为B(_____),D(_____),F(_____).
-4,3
1,-2
1,-1
随堂练习
1.如图,将线段AB绕点O顺时针旋转90°得到线段A′B′,那么A(-2,5)的对应点A′的坐标是( )
A.(2,5)
B.(5,2)
C.(2,-5)
D.(5,-2)
B
2.已知:如图,E(-4,2),F(-1,-1),以O为中心,把△EFO旋转180°,则点E的对应点E′的坐标为(_____________).
4,-2
3.如图是某设计师在方格纸中设计图案的一部分,请你帮他完成余下的工作:
(1)作出关于AB所在直线的轴对称图形;
(2)将你画出的部分连同原图形绕点O逆时针旋转90°;
(3)发挥你的想象,给得到的图案适当涂上阴影,让它变得更加美丽.
[解析] (1)根据轴对称的概念先找到图形上的关键点关于AB所在直线的对称点,然后顺次连接起来即可;(2)将图形的各个顶点绕旋转中心O逆时针旋转90°后的对应点描出来,然后顺次连接起来即可;(3)根据自己的想象恰当地涂色.
解:如图:
[归纳] 利用平移、轴对称、旋转等变换设计图案,一般都是先找“关键点”,再作关键点的对应点,然后顺次连接起来即可.
平移
轴对称
旋转
图形变换的基本方式有哪些?
思考:我们可以将这些图形变换的方式组合起来吗?
知识拓展
你能利用上述方式设计出美丽的图案吗?
课堂小结
1.在平面直角坐标系中,以原点为旋转中心把一个图形按逆时针方向旋转,原图上任意一点坐标(x,y)旋转特定角度后对应点的坐标如下表:
旋转角度 90° 180° 270° 360°
对应点坐标(x,y) ________ ________ ________ ________
(-y,x)
(-x,-y)
(y,-x)
(x,y)
2.把(x,y)变换成__________的变换叫做恒等变换.
(x,y)
谢谢观看
