期末计算题专项:分数四则混合运算(拓展卷)数学六年级上册苏教版(含解析)
文档属性
| 名称 | 期末计算题专项:分数四则混合运算(拓展卷)数学六年级上册苏教版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-27 11:18:03 | ||
图片预览
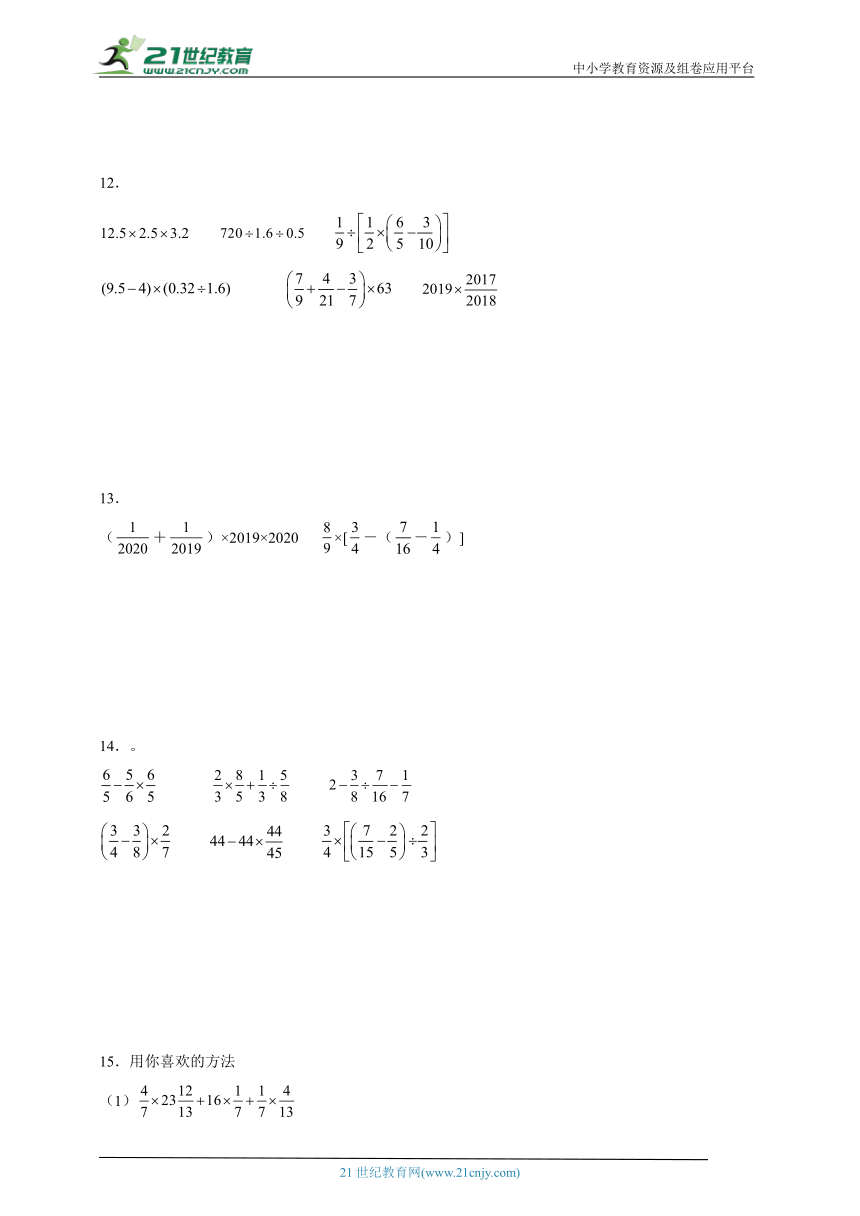

文档简介
中小学教育资源及组卷应用平台
期末计算题专项:分数四则混合运算(拓展卷)数学六年级上册苏教版
1.
2.
3.
+++
4.
1-+-+-+-
5.
(1+)×(1+)×(1+)×…×(1+)×(1+)
6.
(1) (2)
(3) (4)
7.
8.
(1)
(2)
9
3-×-
+×÷2
10.
-× ÷8
÷3+ ÷
11.
12.
13.
(+)×2019×2020 ×[-(-)]
14.。
15.用你喜欢的方法
(1)
(2)
16.
(1)
(2)
17.
18.
;
19.
20.
21.
参考答案:
1.20.20;2013
;123
【分析】第一小题,把原式变为:,再利用乘法分配律即可简算。
第二小题,把2015看作2014与1的和,再利用乘法分配律即可简算。
第三小题,观察发现原式等于:,变为:×,即可简算。
第四小题,观察发现原式等于:,化简算式,即可简算。
【详解】
=
=
=20.20×1
=20.20
=
=
=2013+
=2013
=
=×
=×
=×
=×
=
=
=31+41+51
=123
2.7.5;64;75
【分析】将化成0.75,再利用乘法分配律简算;
利用乘法分配律简算;
按照分数混合运算的顺序,先算小括号里的加法,再算中括号里的乘法,最后算中括号外的除法。
【详解】
=
=
=7.5
=
=34+30
=64
=
=
=75
3.;;
0;;16
【分析】根据裂项法,即原式变为:1-+-+-+-+-+-,由此即可简便运算;
先把带分数化成假分数的形式,即原式变为:2007÷,之后假分数的分母用乘法分配律,即原式变为:2007÷,之后再按照分数除法的计算方法,除以一个数相当于乘一个数的倒数,由此即可简便运算;
+++由于分子都是3,可以运用乘法分配律,即原式变为:3×(+++)之后括号里的式子根据裂项法,即原式变为3×[×(1-+-+-+-)]之后根据运算顺序即可简便运算;
根据分数除法的计算方法,除以一个数相当于乘这个数的倒数,即原式变为:之后运用乘法分配律即可简便运算;
按照运算顺序,先算小括号里的,再算中括号里的,之后算除法,最后算加法即可;
运用乘法交换律和乘法结合律,即原式变为:(68×90)×(),把68×90看作一个整体,之后运用乘法分配律即可简便运算。
【详解】
=1-+-+-+-+-+-
=1-
=
=2007÷
=2007÷
=2007÷
=2007×
=
+++
=3×(+++)
=3×[×(1-+-+-+-)]
=3×[×]
=3××
=
=
=2-(×+×)
=2-(+)
=2-2
=0
=
=
=33+
=
=(68×90)×()
=68×90×+68×90×
=+
=16
4.16;
12;2
【分析】把16拆成4×4,再运用乘法交换律,即原式变为:,之后运用乘法分配律即可简便运算;
1-+-+-+-运用裂项法,即原式变为:(1+)-(+)+(+)-(+)+(+)-(+)+(+)-(+)之后运用减法的性质去括号即可简便运算;
运用乘法交换律和乘法结合律,即原式变为:(75×54)×(),把75×54看作一个整体,之后运用乘法分配律即可简便运算。
把第一个括号里的分数都换成2乘一个数的形式,即原式变为:之后第一个括号里的数运用乘法分配律即可简便运算;
【详解】
=
=×(+4+)
=×28
=16
1-+-+-+-
=(1+)-(+)+(+)-(+)+(+)-(+)+(+)-(+)
=1+--++--++--++--
=1-
=
=(75×54)×()
=75×54×+75×54×
=
=12
=
=2×()÷()
=2
5.
【分析】观察可知,前一个括号里的数加起来的分子,是后一个括号里的数加起来的分母,所以约分抵消后,只剩下第一个括号里算出来的分母,以及最后一个括号里算出来的分子,据此分析。
【详解】(1+)×(1+)×(1+)×…×(1+)×(1+)
=×××…××
=×××…×
=
6.(1);(2)1.25
(3);(4)
【分析】(1)将算式中的除法转化为乘法,再利用乘法分配律简算;
(2)将原算式改写成,再利用乘法分配律简算;
(3)先算乘法,再从左到右,依次计算;
(4)先算括号里的加法,再将算式中的除法转化为乘法,最后从左到右,依次
【详解】(1)
=
=
=
(2)
=
=
=0.125×10
=1.25
(3)
=
=
(4)
=
=
=
7.133;100
【分析】首先把、、分别写成40+、50+、70+,然后根据乘法分配律进行简算;
把除以化成乘,把2.64×12.5写成26.4×1.25的形式,再运用乘法的分配律进行简算。
【详解】
=
=
=30+1+40+1+60+1
=133
=
=
=
=100
8.(1);(2)
【分析】(1)2020÷,把带分数化成假分数,==,原式化为:2020÷,把除法换成乘法,原式化为:2020×,约分,即可解答;
(2)(+++)×(+++)-(++++)×(++),把(+++)化为[(++)+],(++++)化为[(+++)+];原式化为:(+++)×[(++)+]-[(+++)+]×(++),再根据乘法分配律,原式化为:(+++)×(++)+(+++)×-(+++)×(++)-×(++),原式化为:(+++)×-×(++),再根据乘法分配律,原式化为:×(+++---),再进行
【详解】(1)2020÷
=2020÷
=2020÷
=2020×
=
(2)(+++)×(+++)-(++++)×(++)
=(+++)×[(++)+]-[(+++)+]×(++)
=(+++)×(++)+(+++)×-(+++)×(++)-×(++)
=(+++)×-×(++)
=×(+++---)
=×
=
9.;2;
;
【分析】先算小括号里面的减法,再利用乘法分配律进行简算即可;
先算乘法,再利用减法的性质进行简算即可;
先将除法变为乘法,再利用乘法分配律进行简算即可;
先将除法变为乘法,能约分的约分,再进行计算即可。
【详解】
=
=
=
=
3-×-
=
=
=3-1
=2
=
=
=
=
+×÷2
=
=
=
10.;;;
;53;
【分析】将写成11+的形式,然后利用乘法分配律进行简算;
按照分数混合运算的顺序,先算乘除法,再算减法;
运用乘法分配律进行简算;
将原式中的除法写成乘法的形式,然后运用乘法分配律进行简算;
将原式中的除法写成乘法的形式,然后运用乘法分配律进行简算;
运用乘法分配律进行简算。
【详解】-×
=11+×1-×
=11+×(1-)
=11+×
=
÷8
=-2÷8
=-
=
=40×-×
=30-
=
÷3+
=×+
=×(+)
=
÷
=×72
=
=63-16+6
=53
=×(-)
=
11.6;;1;
;;17
【分析】第一小题中除以一个分数相当于乘它的倒数,再运用分数乘法的提取相同因数计算;第二小题中可先将分数除法化为乘法,再进行计算;第三小题中按照分数的四则混合运算法则进行计算;第四小题中可将96化为97-1,再进行计算;第五小题按照分数的四则混合运算法则计算;第六小题化为乘法后,运用分配律进行
【详解】
;
;
;
;
;
。
12.100,900,
1.1,34,
【分析】将3.2写成0.4×8的形式,再利用乘法结合律进行简算;
根据除法的性质,先算1.6和0.5的积,再用720除以这个积;
根据运算顺序,先算小括号里,再算中括号里,最后算中括号外面;
先算小括号里,最后算乘法;
根据乘法分配律进行简算;
将2019写成(2018+1)的形式,再根据乘法分配律进行简算
【详解】12.5×2.5×3.2
=12.5×2.5×0.4×8
=12.5×8×(2.5×0.4)
=100×1
=100
720÷1.6÷0.5
=720÷(1.6×0.5)
=720÷0.8
=900
÷[×(-)]
=÷[×]
=÷
=
=5.5×0.2
=1.1
=
=49+12-27
=34
2019×
=(2018+1)×
=2018×+1×
=2017+
=
【点睛】本题综合考查了运算定律与简便运算,四则混合运算。注意运算顺序和运算法则,灵活运用所学的运算定律
13.4039;
【分析】运用了乘法分配律来简便计算;
括号中运用了减法性质来
【详解】(+)×2019×2020
=×2019×2020+×2019×2020
=2019+2020
=4039
×[-(-)]
=×[+-]
=×[1-]
=×
=
14.;;1
;;
【分析】第1题,先算乘法,再算减法;第2题,除法变乘法,提取公因数简便计算;第3题,先算除法,再算减法;第4题,先算括号里面的,再算括号外面的;第5题,把44作为公因数,提取公因数简便计算;第6题,先算小括号里面的,再算中括号里面的,最后算括号外面的。
【详解】
15.(1)16;(2)3
【分析】(1)把拆成(),变成, 变成,然后利用乘法分配律计算即可;
(2)把写成,然后把整体写成分数的形式,分子分母约分即可。
【详解】(1)
(2)
【点睛】本题重点考查分数的四则混合运算计算法则及简便方法的使用。
16.(1) ;(2)
【分析】(1)把每一项都写成两个分数相减的形式,最后把中间的相互抵消,计算即可。
(2)把每一项都写成 与两个分数的差相乘的形式,利用乘法分配律,把提取出来,剩下的一个因数相加,中间的可以相互抵消,据此
【详解】(1)
= …+
=1-
= ;
(2)
=×( … )
=×( )
=
【点睛】认真观察算式,找出其中的规律,通过裂项抵消的方法计算即可。
17.41;1;14;3
【分析】根据符号特点和数据特点选择合适的运算定律进行
【详解】
18.;;
;;
【分析】根据数据特点和符号特点选择合适的运算定律进行简便计算;把分数除法转化成分数乘法
【详解】
。
。
。
19.0;180
10;
【分析】-(+)-,根据减法性质,原式化为:---,再根据加法交换律,原式化为:---,再根据加法结合律和减法性质,原式化为:(-)-(+),再进行计算;
36×2.54+1.8×49.2,把36化为1.8×20;原式化为:1.8×20×2.54+1.8×49.2,再根据乘法分配律,原式化为:1.8×(20×2.54+49.2),再进行计算;
÷+5.46÷×(4.875-),把小数化成分数,5.46=;4.875=;原式化为:÷+÷×(-),再根据分数四则混合运算的计算法则,进行计算即可。
1+++++,把化为3+;=5+;=7+;=9+;化为11+;原式化为:1+3++5++7++9++11+;再根据加法交换律,原式化为:1+3+5+7+9+11+++++,再根据加法结合律,原式化为:(1+3+5+7+9+11)+(++++),把化为-;化为-;化为-;=-;=-;原式化为:(1+3+5+7+9+11)+(-+-+-+-+-),再进行
【详解】-(+)-
=---
=---
=(-)-(+)
=7-7
=0
36×2.54+1.8×49.2
=1.8×20×2.54+1.8×49.2
=1.8×(20×2.54+49.2)
=1.8×(50.8+49.2)
=1.8×100
=180
÷+5.46÷×(4.875-)
=÷+÷×(-)
=÷+÷×2
=×+××2
=+×2
=+
=10
1+++++
=1+3++5++7++9++11+
=1+3+5+7+9+11+++++
=(1+3+5+7+9+11)+(++++)
=(4+5+7+9+11)+(-+-+-+-+-)
=(9+7+9+11)+(-)
=(16+9+11)+(-)
=(25+11)+
=36+
=
20.1;
【分析】,先把分母的375拆分为374+1,然后根据乘法分配律,将算式变为,然后计算543×1,再加上括号,将算式变为,然后计算出括号里面的减法,最后约分即可。
,先根据带分数化假分数的方法,将算式变为,然后将除法化为乘法,算式变为,也就是,根据乘法分配律,将算式变为,再计算出括号里面的加法;然后根据整数乘分数的方法进行计算即可。
【详解】
21.;1
【分析】(1)先把带分数换成假分数,再根据乘法分配律计算,最后把除法换成乘法计算即可。
(2)先把1987看成(1988-1),再根据乘法分配律计算即可。
【详解】(1)
=
=
=
=
=
(2)
=
=
=
=1
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末计算题专项:分数四则混合运算(拓展卷)数学六年级上册苏教版
1.
2.
3.
+++
4.
1-+-+-+-
5.
(1+)×(1+)×(1+)×…×(1+)×(1+)
6.
(1) (2)
(3) (4)
7.
8.
(1)
(2)
9
3-×-
+×÷2
10.
-× ÷8
÷3+ ÷
11.
12.
13.
(+)×2019×2020 ×[-(-)]
14.。
15.用你喜欢的方法
(1)
(2)
16.
(1)
(2)
17.
18.
;
19.
20.
21.
参考答案:
1.20.20;2013
;123
【分析】第一小题,把原式变为:,再利用乘法分配律即可简算。
第二小题,把2015看作2014与1的和,再利用乘法分配律即可简算。
第三小题,观察发现原式等于:,变为:×,即可简算。
第四小题,观察发现原式等于:,化简算式,即可简算。
【详解】
=
=
=20.20×1
=20.20
=
=
=2013+
=2013
=
=×
=×
=×
=×
=
=
=31+41+51
=123
2.7.5;64;75
【分析】将化成0.75,再利用乘法分配律简算;
利用乘法分配律简算;
按照分数混合运算的顺序,先算小括号里的加法,再算中括号里的乘法,最后算中括号外的除法。
【详解】
=
=
=7.5
=
=34+30
=64
=
=
=75
3.;;
0;;16
【分析】根据裂项法,即原式变为:1-+-+-+-+-+-,由此即可简便运算;
先把带分数化成假分数的形式,即原式变为:2007÷,之后假分数的分母用乘法分配律,即原式变为:2007÷,之后再按照分数除法的计算方法,除以一个数相当于乘一个数的倒数,由此即可简便运算;
+++由于分子都是3,可以运用乘法分配律,即原式变为:3×(+++)之后括号里的式子根据裂项法,即原式变为3×[×(1-+-+-+-)]之后根据运算顺序即可简便运算;
根据分数除法的计算方法,除以一个数相当于乘这个数的倒数,即原式变为:之后运用乘法分配律即可简便运算;
按照运算顺序,先算小括号里的,再算中括号里的,之后算除法,最后算加法即可;
运用乘法交换律和乘法结合律,即原式变为:(68×90)×(),把68×90看作一个整体,之后运用乘法分配律即可简便运算。
【详解】
=1-+-+-+-+-+-
=1-
=
=2007÷
=2007÷
=2007÷
=2007×
=
+++
=3×(+++)
=3×[×(1-+-+-+-)]
=3×[×]
=3××
=
=
=2-(×+×)
=2-(+)
=2-2
=0
=
=
=33+
=
=(68×90)×()
=68×90×+68×90×
=+
=16
4.16;
12;2
【分析】把16拆成4×4,再运用乘法交换律,即原式变为:,之后运用乘法分配律即可简便运算;
1-+-+-+-运用裂项法,即原式变为:(1+)-(+)+(+)-(+)+(+)-(+)+(+)-(+)之后运用减法的性质去括号即可简便运算;
运用乘法交换律和乘法结合律,即原式变为:(75×54)×(),把75×54看作一个整体,之后运用乘法分配律即可简便运算。
把第一个括号里的分数都换成2乘一个数的形式,即原式变为:之后第一个括号里的数运用乘法分配律即可简便运算;
【详解】
=
=×(+4+)
=×28
=16
1-+-+-+-
=(1+)-(+)+(+)-(+)+(+)-(+)+(+)-(+)
=1+--++--++--++--
=1-
=
=(75×54)×()
=75×54×+75×54×
=
=12
=
=2×()÷()
=2
5.
【分析】观察可知,前一个括号里的数加起来的分子,是后一个括号里的数加起来的分母,所以约分抵消后,只剩下第一个括号里算出来的分母,以及最后一个括号里算出来的分子,据此分析。
【详解】(1+)×(1+)×(1+)×…×(1+)×(1+)
=×××…××
=×××…×
=
6.(1);(2)1.25
(3);(4)
【分析】(1)将算式中的除法转化为乘法,再利用乘法分配律简算;
(2)将原算式改写成,再利用乘法分配律简算;
(3)先算乘法,再从左到右,依次计算;
(4)先算括号里的加法,再将算式中的除法转化为乘法,最后从左到右,依次
【详解】(1)
=
=
=
(2)
=
=
=0.125×10
=1.25
(3)
=
=
(4)
=
=
=
7.133;100
【分析】首先把、、分别写成40+、50+、70+,然后根据乘法分配律进行简算;
把除以化成乘,把2.64×12.5写成26.4×1.25的形式,再运用乘法的分配律进行简算。
【详解】
=
=
=30+1+40+1+60+1
=133
=
=
=
=100
8.(1);(2)
【分析】(1)2020÷,把带分数化成假分数,==,原式化为:2020÷,把除法换成乘法,原式化为:2020×,约分,即可解答;
(2)(+++)×(+++)-(++++)×(++),把(+++)化为[(++)+],(++++)化为[(+++)+];原式化为:(+++)×[(++)+]-[(+++)+]×(++),再根据乘法分配律,原式化为:(+++)×(++)+(+++)×-(+++)×(++)-×(++),原式化为:(+++)×-×(++),再根据乘法分配律,原式化为:×(+++---),再进行
【详解】(1)2020÷
=2020÷
=2020÷
=2020×
=
(2)(+++)×(+++)-(++++)×(++)
=(+++)×[(++)+]-[(+++)+]×(++)
=(+++)×(++)+(+++)×-(+++)×(++)-×(++)
=(+++)×-×(++)
=×(+++---)
=×
=
9.;2;
;
【分析】先算小括号里面的减法,再利用乘法分配律进行简算即可;
先算乘法,再利用减法的性质进行简算即可;
先将除法变为乘法,再利用乘法分配律进行简算即可;
先将除法变为乘法,能约分的约分,再进行计算即可。
【详解】
=
=
=
=
3-×-
=
=
=3-1
=2
=
=
=
=
+×÷2
=
=
=
10.;;;
;53;
【分析】将写成11+的形式,然后利用乘法分配律进行简算;
按照分数混合运算的顺序,先算乘除法,再算减法;
运用乘法分配律进行简算;
将原式中的除法写成乘法的形式,然后运用乘法分配律进行简算;
将原式中的除法写成乘法的形式,然后运用乘法分配律进行简算;
运用乘法分配律进行简算。
【详解】-×
=11+×1-×
=11+×(1-)
=11+×
=
÷8
=-2÷8
=-
=
=40×-×
=30-
=
÷3+
=×+
=×(+)
=
÷
=×72
=
=63-16+6
=53
=×(-)
=
11.6;;1;
;;17
【分析】第一小题中除以一个分数相当于乘它的倒数,再运用分数乘法的提取相同因数计算;第二小题中可先将分数除法化为乘法,再进行计算;第三小题中按照分数的四则混合运算法则进行计算;第四小题中可将96化为97-1,再进行计算;第五小题按照分数的四则混合运算法则计算;第六小题化为乘法后,运用分配律进行
【详解】
;
;
;
;
;
。
12.100,900,
1.1,34,
【分析】将3.2写成0.4×8的形式,再利用乘法结合律进行简算;
根据除法的性质,先算1.6和0.5的积,再用720除以这个积;
根据运算顺序,先算小括号里,再算中括号里,最后算中括号外面;
先算小括号里,最后算乘法;
根据乘法分配律进行简算;
将2019写成(2018+1)的形式,再根据乘法分配律进行简算
【详解】12.5×2.5×3.2
=12.5×2.5×0.4×8
=12.5×8×(2.5×0.4)
=100×1
=100
720÷1.6÷0.5
=720÷(1.6×0.5)
=720÷0.8
=900
÷[×(-)]
=÷[×]
=÷
=
=5.5×0.2
=1.1
=
=49+12-27
=34
2019×
=(2018+1)×
=2018×+1×
=2017+
=
【点睛】本题综合考查了运算定律与简便运算,四则混合运算。注意运算顺序和运算法则,灵活运用所学的运算定律
13.4039;
【分析】运用了乘法分配律来简便计算;
括号中运用了减法性质来
【详解】(+)×2019×2020
=×2019×2020+×2019×2020
=2019+2020
=4039
×[-(-)]
=×[+-]
=×[1-]
=×
=
14.;;1
;;
【分析】第1题,先算乘法,再算减法;第2题,除法变乘法,提取公因数简便计算;第3题,先算除法,再算减法;第4题,先算括号里面的,再算括号外面的;第5题,把44作为公因数,提取公因数简便计算;第6题,先算小括号里面的,再算中括号里面的,最后算括号外面的。
【详解】
15.(1)16;(2)3
【分析】(1)把拆成(),变成, 变成,然后利用乘法分配律计算即可;
(2)把写成,然后把整体写成分数的形式,分子分母约分即可。
【详解】(1)
(2)
【点睛】本题重点考查分数的四则混合运算计算法则及简便方法的使用。
16.(1) ;(2)
【分析】(1)把每一项都写成两个分数相减的形式,最后把中间的相互抵消,计算即可。
(2)把每一项都写成 与两个分数的差相乘的形式,利用乘法分配律,把提取出来,剩下的一个因数相加,中间的可以相互抵消,据此
【详解】(1)
= …+
=1-
= ;
(2)
=×( … )
=×( )
=
【点睛】认真观察算式,找出其中的规律,通过裂项抵消的方法计算即可。
17.41;1;14;3
【分析】根据符号特点和数据特点选择合适的运算定律进行
【详解】
18.;;
;;
【分析】根据数据特点和符号特点选择合适的运算定律进行简便计算;把分数除法转化成分数乘法
【详解】
。
。
。
19.0;180
10;
【分析】-(+)-,根据减法性质,原式化为:---,再根据加法交换律,原式化为:---,再根据加法结合律和减法性质,原式化为:(-)-(+),再进行计算;
36×2.54+1.8×49.2,把36化为1.8×20;原式化为:1.8×20×2.54+1.8×49.2,再根据乘法分配律,原式化为:1.8×(20×2.54+49.2),再进行计算;
÷+5.46÷×(4.875-),把小数化成分数,5.46=;4.875=;原式化为:÷+÷×(-),再根据分数四则混合运算的计算法则,进行计算即可。
1+++++,把化为3+;=5+;=7+;=9+;化为11+;原式化为:1+3++5++7++9++11+;再根据加法交换律,原式化为:1+3+5+7+9+11+++++,再根据加法结合律,原式化为:(1+3+5+7+9+11)+(++++),把化为-;化为-;化为-;=-;=-;原式化为:(1+3+5+7+9+11)+(-+-+-+-+-),再进行
【详解】-(+)-
=---
=---
=(-)-(+)
=7-7
=0
36×2.54+1.8×49.2
=1.8×20×2.54+1.8×49.2
=1.8×(20×2.54+49.2)
=1.8×(50.8+49.2)
=1.8×100
=180
÷+5.46÷×(4.875-)
=÷+÷×(-)
=÷+÷×2
=×+××2
=+×2
=+
=10
1+++++
=1+3++5++7++9++11+
=1+3+5+7+9+11+++++
=(1+3+5+7+9+11)+(++++)
=(4+5+7+9+11)+(-+-+-+-+-)
=(9+7+9+11)+(-)
=(16+9+11)+(-)
=(25+11)+
=36+
=
20.1;
【分析】,先把分母的375拆分为374+1,然后根据乘法分配律,将算式变为,然后计算543×1,再加上括号,将算式变为,然后计算出括号里面的减法,最后约分即可。
,先根据带分数化假分数的方法,将算式变为,然后将除法化为乘法,算式变为,也就是,根据乘法分配律,将算式变为,再计算出括号里面的加法;然后根据整数乘分数的方法进行计算即可。
【详解】
21.;1
【分析】(1)先把带分数换成假分数,再根据乘法分配律计算,最后把除法换成乘法计算即可。
(2)先把1987看成(1988-1),再根据乘法分配律计算即可。
【详解】(1)
=
=
=
=
=
(2)
=
=
=
=1
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
