29.2 直线与圆的位置关系 课件(共15张PPT) 冀教版数学九年级下册
文档属性
| 名称 | 29.2 直线与圆的位置关系 课件(共15张PPT) 冀教版数学九年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-27 00:00:00 | ||
图片预览




文档简介
(共15张PPT)
第二十九章 直线与圆的位置关系
29.2 直线与圆的位置关系
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1.理解掌握直线与圆的三种位置关系
2.理解直线与圆三种位置关系的性质,并解决简单问题(重点)
典型例题
当堂检测
学习目标
课堂总结
概念剖析
看一看:观察下图中图形,试着发现它们的规律。
太阳即将升起,在地平线以下
太阳升起后,与水平线相离
情景引入
典型例题
当堂检测
学习目标
课堂总结
概念剖析
太阳刚升起,与水平线逐渐远离
看一看:观察下图中图形,试着发现它们的规律。
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1
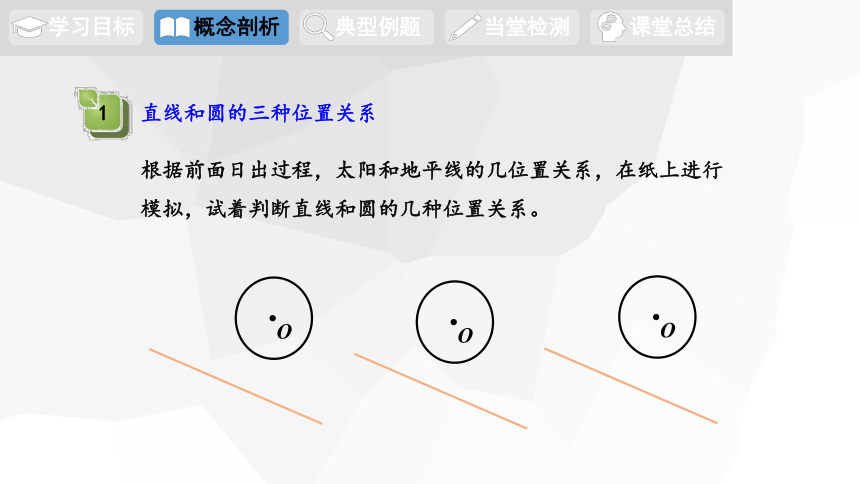
直线和圆的三种位置关系
根据前面日出过程,太阳和地平线的几位置关系,在纸上进行模拟,试着判断直线和圆的几种位置关系。
O
O
O
典型例题
当堂检测
学习目标
课堂总结
概念剖析
O
O
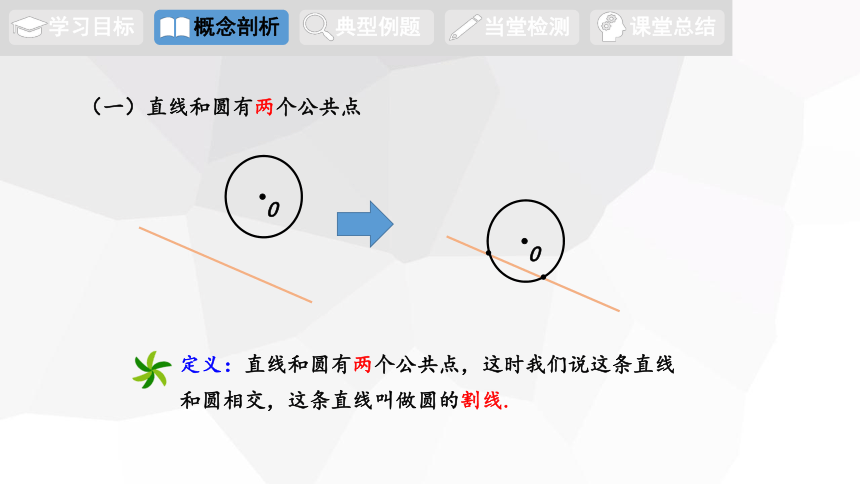
(一)直线和圆有两个公共点
定义:直线和圆有两个公共点,这时我们说这条直线和圆相交,这条直线叫做圆的割线.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
O
O
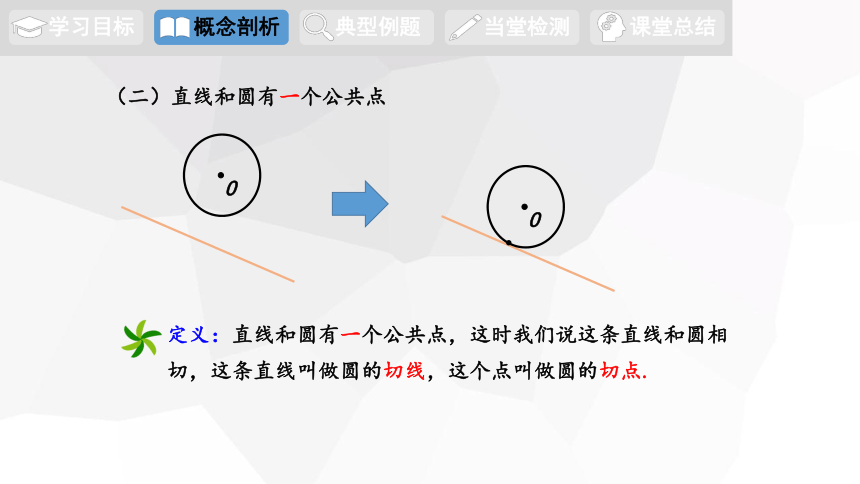
(二)直线和圆有一个公共点
定义:直线和圆有一个公共点,这时我们说这条直线和圆相切,这条直线叫做圆的切线,这个点叫做圆的切点.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
O
O
(三)直线和圆没有公共点
定义:直线和圆没有公共点,这时我们说这条直线和圆相离.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
(1)直线与圆最多有两个公共点.
(2)若直线与圆相交,则直线上的点都在圆上.
(3)若A是⊙O上一点,则直线AB与⊙O相切.
(4)若C为⊙O外一点,则过点C的直线与⊙O相交或相离.
(5)直线a 和⊙O有公共点,则直线a与⊙O相交.
例1.判断正误:
√
×
×
×
×
小提示:初步判断直线与圆的位置关系可将“公共点的个数”作为依据!
典型例题
当堂检测
学习目标
课堂总结
概念剖析
.O
.O
.O
.O
.O
1.看图判断直线l与☉O的位置关系:
(1)
(2)
(3)
(4)
(5)
相离
相交
相切
相交
注意:直线是可以无限延伸的.
相交
典型例题
当堂检测
学习目标
课堂总结
概念剖析
2
直线和圆的位置关系的性质
根据直线和圆相交、相切、相离的定义,容易得到:
直线和圆相交 ___________
直线和圆相切 ___________
直线和圆相离 ___________
d>r
d=r
dO
d
r
O
r
d
O
d
r
典型例题
当堂检测
学习目标
课堂总结
概念剖析
例2.如图,Rt△ABC的斜边AB=10cm,∠A=30°.
(1) 以点C为圆心,当半径为多少时,AB与☉C相切?
(2) 以点C为圆心,半径r分别为4cm,5cm作两个圆,这两个圆与斜边AB分别有怎样的位置关系?
A
C
B
解:(1) 过点C作边AB上的高CD.
D
∵∠A=30°,AB=10cm,
在Rt△BCD中,有
当半径为 时,AB与☉C相切.
(2)r=4<CD,此时圆与斜边AB相离
r=5>CD,此时圆与斜边AB相交
典型例题
当堂检测
学习目标
课堂总结
概念剖析
2.在平面直角坐标系中,以点(3,2)为圆心,3为半径的圆,一定( )
A.与x轴相切,与y轴相切
B.与x轴相切,与y轴相交
C.与x轴相交,与y轴相切
D.与x轴相交,与y轴相交
C
典型例题
当堂检测
学习目标
课堂总结
概念剖析
3.△ABC中,∠C=90°,AC=4,BC=3,以点C为圆心,以R长为半径画圆,若☉C与AB相交,求R的范围.
解:过点C作CD垂直于AB,
∵∠ACB=90°,AC=4,BC=3,
由勾股定理得:AB= =5
由面积公式得: AC·BC= AB·CD,
∴当2.4D
典型例题
当堂检测
学习目标
课堂总结
概念剖析
直线与圆的位置关系
定义
性质
判定
相离
相切
相交
公共点的个数
d与r的数量关系
定义法
性质法
相离:0个
相切:1个
相交:2个
相离:d>r
相切:d=r
相交:d0个:相离;1个:相切;2个:相交
d>r:相离
d=r:相切
d
第二十九章 直线与圆的位置关系
29.2 直线与圆的位置关系
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1.理解掌握直线与圆的三种位置关系
2.理解直线与圆三种位置关系的性质,并解决简单问题(重点)
典型例题
当堂检测
学习目标
课堂总结
概念剖析
看一看:观察下图中图形,试着发现它们的规律。
太阳即将升起,在地平线以下
太阳升起后,与水平线相离
情景引入
典型例题
当堂检测
学习目标
课堂总结
概念剖析
太阳刚升起,与水平线逐渐远离
看一看:观察下图中图形,试着发现它们的规律。
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1
直线和圆的三种位置关系
根据前面日出过程,太阳和地平线的几位置关系,在纸上进行模拟,试着判断直线和圆的几种位置关系。
O
O
O
典型例题
当堂检测
学习目标
课堂总结
概念剖析
O
O
(一)直线和圆有两个公共点
定义:直线和圆有两个公共点,这时我们说这条直线和圆相交,这条直线叫做圆的割线.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
O
O
(二)直线和圆有一个公共点
定义:直线和圆有一个公共点,这时我们说这条直线和圆相切,这条直线叫做圆的切线,这个点叫做圆的切点.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
O
O
(三)直线和圆没有公共点
定义:直线和圆没有公共点,这时我们说这条直线和圆相离.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
(1)直线与圆最多有两个公共点.
(2)若直线与圆相交,则直线上的点都在圆上.
(3)若A是⊙O上一点,则直线AB与⊙O相切.
(4)若C为⊙O外一点,则过点C的直线与⊙O相交或相离.
(5)直线a 和⊙O有公共点,则直线a与⊙O相交.
例1.判断正误:
√
×
×
×
×
小提示:初步判断直线与圆的位置关系可将“公共点的个数”作为依据!
典型例题
当堂检测
学习目标
课堂总结
概念剖析
.O
.O
.O
.O
.O
1.看图判断直线l与☉O的位置关系:
(1)
(2)
(3)
(4)
(5)
相离
相交
相切
相交
注意:直线是可以无限延伸的.
相交
典型例题
当堂检测
学习目标
课堂总结
概念剖析
2
直线和圆的位置关系的性质
根据直线和圆相交、相切、相离的定义,容易得到:
直线和圆相交 ___________
直线和圆相切 ___________
直线和圆相离 ___________
d>r
d=r
d
d
r
O
r
d
O
d
r
典型例题
当堂检测
学习目标
课堂总结
概念剖析
例2.如图,Rt△ABC的斜边AB=10cm,∠A=30°.
(1) 以点C为圆心,当半径为多少时,AB与☉C相切?
(2) 以点C为圆心,半径r分别为4cm,5cm作两个圆,这两个圆与斜边AB分别有怎样的位置关系?
A
C
B
解:(1) 过点C作边AB上的高CD.
D
∵∠A=30°,AB=10cm,
在Rt△BCD中,有
当半径为 时,AB与☉C相切.
(2)r=4<CD,此时圆与斜边AB相离
r=5>CD,此时圆与斜边AB相交
典型例题
当堂检测
学习目标
课堂总结
概念剖析
2.在平面直角坐标系中,以点(3,2)为圆心,3为半径的圆,一定( )
A.与x轴相切,与y轴相切
B.与x轴相切,与y轴相交
C.与x轴相交,与y轴相切
D.与x轴相交,与y轴相交
C
典型例题
当堂检测
学习目标
课堂总结
概念剖析
3.△ABC中,∠C=90°,AC=4,BC=3,以点C为圆心,以R长为半径画圆,若☉C与AB相交,求R的范围.
解:过点C作CD垂直于AB,
∵∠ACB=90°,AC=4,BC=3,
由勾股定理得:AB= =5
由面积公式得: AC·BC= AB·CD,
∴当2.4
典型例题
当堂检测
学习目标
课堂总结
概念剖析
直线与圆的位置关系
定义
性质
判定
相离
相切
相交
公共点的个数
d与r的数量关系
定义法
性质法
相离:0个
相切:1个
相交:2个
相离:d>r
相切:d=r
相交:d
d>r:相离
d=r:相切
d
