冀教版九年级数学下册 32.2 视图 第3课时课件(共15张PPT)
文档属性
| 名称 | 冀教版九年级数学下册 32.2 视图 第3课时课件(共15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-27 18:26:59 | ||
图片预览



文档简介
(共15张PPT)
第三十二章 投影与视图
32.2 视图
第3课时
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1.进一步明确三视图的意义,由三视图想象出原型(重点)
2.由三视图得出实物原型并进行简单计算
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1
由三视图还原几何体
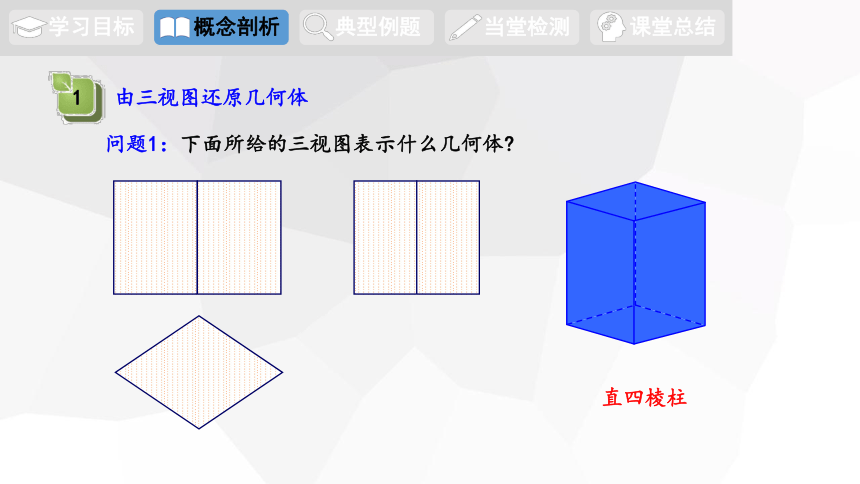
问题1:下面所给的三视图表示什么几何体
直四棱柱
典型例题
当堂检测
学习目标
课堂总结
概念剖析
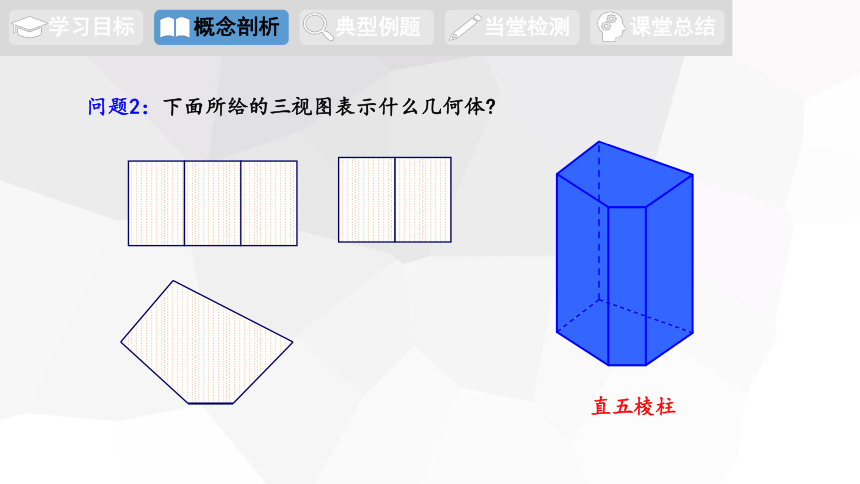
问题2:下面所给的三视图表示什么几何体
直五棱柱
典型例题
当堂检测
学习目标
课堂总结
概念剖析
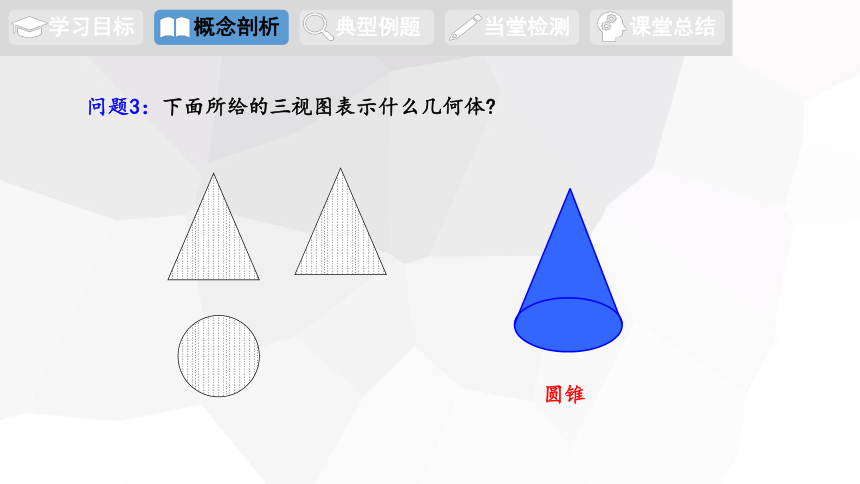
问题3:下面所给的三视图表示什么几何体
圆锥
典型例题
当堂检测
学习目标
课堂总结
概念剖析
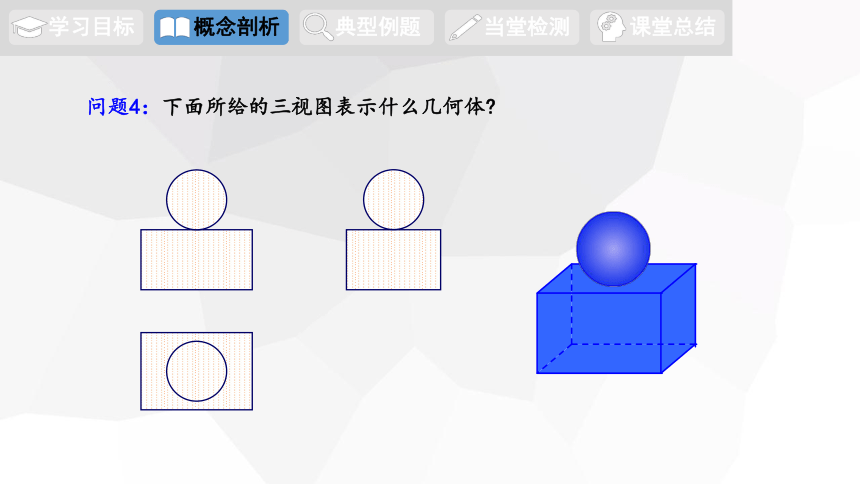
问题4:下面所给的三视图表示什么几何体
典型例题
当堂检测
学习目标
课堂总结
概念剖析
归纳总结:
由三视图描述几何体的一般步骤:
① 想象:根据各视图想象从各个方向看到的几何体形状;
② 定形:综合确定几何体(或实物原型)的形状;
③ 定大小位置:根据三个视图“长对正,高平齐,宽相等”的关系,确定轮廓线的位置,以及各个方向的尺寸.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
例1:根据下列图中所给出的一个物体的三视图,试画出它的形状.
解:图(1)所对应的几何体为一个三棱柱如图①,
典型例题
当堂检测
学习目标
课堂总结
概念剖析
解:图(2)所对应的几何体如图②.
根据下列图中所给出的一个物体的三视图,试画出它的形状.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1.一个几何体的三视图如图所示,则该几何体是( )
D
典型例题
当堂检测
学习目标
课堂总结
概念剖析
2
与三视图有关的计算
例2:某几何体的主视图、左视图和俯视图分别如图,求该几何体的体积?
解:根据三视图可以判断该几何体为圆柱,
圆柱的底面半径为1,高为3,
故体积为:
典型例题
当堂检测
学习目标
课堂总结
概念剖析
归纳总结:
由三视图求立体图形的面积的方法:
(1)先根据给出的三视图确定立体图形,并确定立体图形的长、宽、高.
(2)将立体图形展开成一个平面图形 (展开图),观察它的组成部分.
(3)最后根据已知数据,求出展开图的面积.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
2.长方体的主视图与左视图如图所示(单位:cm),则其俯视图的面积是( )
A.12 cm2 B.8 cm2 C.6 cm2 D.4 cm2
A
典型例题
当堂检测
学习目标
课堂总结
概念剖析
3.如图所示是一个几何体的两种视图,求该几何体的体积(π取3.14).
解:从主、俯视图,我们可想象这是一个长方体上面正中间放一个圆柱
∴该几何体的体积约是40048cm3.
∴V=V圆柱+V长方体
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1.由三视图还原简单几何体
(1)根据主视图、俯视图和左视图想象几何体的正面、上面和左面的形状以及几何体的长、宽、高;
(2)从实线和虚线想象几何体看得见的部分和看不见的部分的轮廓线;
(3)还需要注意几何体的摆放位置.
2.与三视图有关的计算
第三十二章 投影与视图
32.2 视图
第3课时
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1.进一步明确三视图的意义,由三视图想象出原型(重点)
2.由三视图得出实物原型并进行简单计算
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1
由三视图还原几何体
问题1:下面所给的三视图表示什么几何体
直四棱柱
典型例题
当堂检测
学习目标
课堂总结
概念剖析
问题2:下面所给的三视图表示什么几何体
直五棱柱
典型例题
当堂检测
学习目标
课堂总结
概念剖析
问题3:下面所给的三视图表示什么几何体
圆锥
典型例题
当堂检测
学习目标
课堂总结
概念剖析
问题4:下面所给的三视图表示什么几何体
典型例题
当堂检测
学习目标
课堂总结
概念剖析
归纳总结:
由三视图描述几何体的一般步骤:
① 想象:根据各视图想象从各个方向看到的几何体形状;
② 定形:综合确定几何体(或实物原型)的形状;
③ 定大小位置:根据三个视图“长对正,高平齐,宽相等”的关系,确定轮廓线的位置,以及各个方向的尺寸.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
例1:根据下列图中所给出的一个物体的三视图,试画出它的形状.
解:图(1)所对应的几何体为一个三棱柱如图①,
典型例题
当堂检测
学习目标
课堂总结
概念剖析
解:图(2)所对应的几何体如图②.
根据下列图中所给出的一个物体的三视图,试画出它的形状.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1.一个几何体的三视图如图所示,则该几何体是( )
D
典型例题
当堂检测
学习目标
课堂总结
概念剖析
2
与三视图有关的计算
例2:某几何体的主视图、左视图和俯视图分别如图,求该几何体的体积?
解:根据三视图可以判断该几何体为圆柱,
圆柱的底面半径为1,高为3,
故体积为:
典型例题
当堂检测
学习目标
课堂总结
概念剖析
归纳总结:
由三视图求立体图形的面积的方法:
(1)先根据给出的三视图确定立体图形,并确定立体图形的长、宽、高.
(2)将立体图形展开成一个平面图形 (展开图),观察它的组成部分.
(3)最后根据已知数据,求出展开图的面积.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
2.长方体的主视图与左视图如图所示(单位:cm),则其俯视图的面积是( )
A.12 cm2 B.8 cm2 C.6 cm2 D.4 cm2
A
典型例题
当堂检测
学习目标
课堂总结
概念剖析
3.如图所示是一个几何体的两种视图,求该几何体的体积(π取3.14).
解:从主、俯视图,我们可想象这是一个长方体上面正中间放一个圆柱
∴该几何体的体积约是40048cm3.
∴V=V圆柱+V长方体
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1.由三视图还原简单几何体
(1)根据主视图、俯视图和左视图想象几何体的正面、上面和左面的形状以及几何体的长、宽、高;
(2)从实线和虚线想象几何体看得见的部分和看不见的部分的轮廓线;
(3)还需要注意几何体的摆放位置.
2.与三视图有关的计算
