第二章 几何图形的初步认识 复习课课件(共36张PPT) 冀教版七年级数学上册
文档属性
| 名称 | 第二章 几何图形的初步认识 复习课课件(共36张PPT) 冀教版七年级数学上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-27 18:29:54 | ||
图片预览










文档简介
(共36张PPT)
第二章 几何图形的初步认识
第二章 复习课
1.能说出常见的几何体和平面图形的名称,知道点、线、面是构成几何图形的基本元素.
2.能区别线段、射线和直线,明白两点间距离的概念;知道线段、角的表示方法,并会进行度、分、秒的换算;会作一个角等于已知角、作一条线段等于已知线段;知道点与直线的位置关系.
3.知道线段中点及角平分线的含义,并会进行相关的计算.
4.熟记两个基本事实,并能应用它们解决实际问题.
5.知道旋转的概念,熟记旋转的性质.
◎重点:两点间的距离、线段中点、角平分线的概念,线段和角的有关计算.
◎难点:能熟练地进行线段和角的计算,并在实际问题中灵活应用.
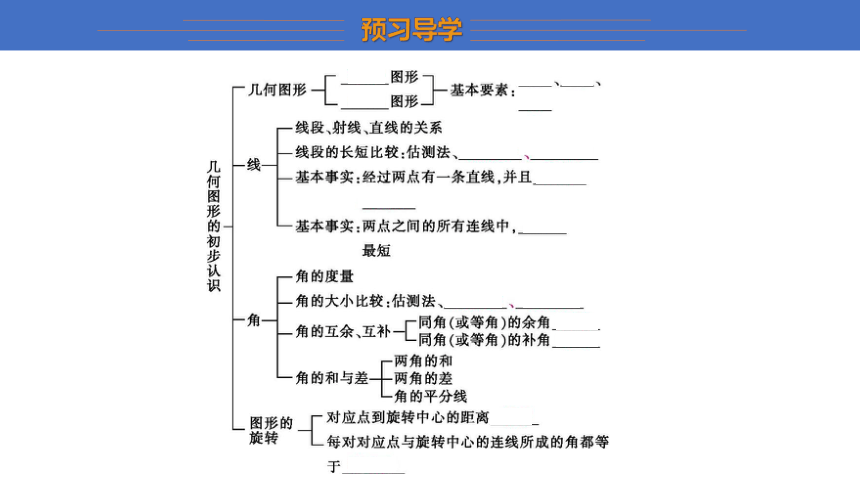
请回顾一下,这一章我们都学习了哪些知识?
请你完成本章的知识网络图.
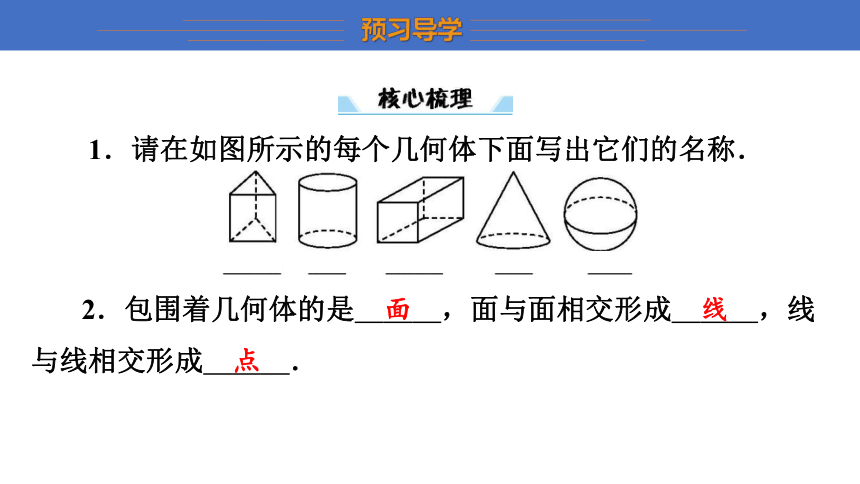
1.请在如图所示的每个几何体下面写出它们的名称.
2.包围着几何体的是 面 ,面与面相交形成 线 ,线与线相交形成 点 .
面
线
点
3.点与直线的位置关系有: 点在直线上(直线经过点) 、 点在直线外(直线不经过点) .
4.两点之间 线段的长度 ,叫做两点之间的距离.
5.有公共 端点 的两条 射线 组成的图形叫做角.
6.如果从一个角的顶点引出的一条 射线 把这个角分成的两个角 相等 ,那么这条 射线 叫做这个角的平分线.
点在直线上(直线经过
点)
点在直线外(直线不经过点)
线段的长度
端点
射线
射线
相等
射线
7.角的度量单位: 度 、 分 、 秒 ,它们之间的关系是:1°= 60 '= 3600 ″;1'= 60 ″;1'= () °;1″= ( '.
度
分
秒
60
3600
60
()
()
8.在平面内,一个图形绕一个 定点 沿某个 方向 转过一个 角度 ,这样的图形运动叫做旋转.这个 定点 叫做旋转中心, 转过的这个角 叫做旋转角.
·导学建议·
预习导学部分可以教师提问学生回答的形式完成,建议学生在课前对不熟悉的知识自己复习,预习导学部分建议教师用10分钟左右的时间完成.
定点
方向
角度
定点
转过的这个角
立体图形与平面图形
1.在圆柱、圆锥、正方体、长方体、棱柱、棱锥、球中,表面有曲面的有 圆柱、圆锥、球 ,只有两个面的有 圆锥 .
圆柱、圆锥、球
圆锥
2.观察下图,回答下列问题.
(1)这个几何体的名称是 六棱柱 .
(2)这个几何体由 6 个侧面, 2 个底面围成,它们分别是 长方 形和 六边 形,这些面都是 平 的.
(3)这个几何体有 18 条棱, 12 个顶点.
六棱柱
6
2
长方
六边
平
18
12
(4)侧面的个数与底面多边形边数的关系是 相等 .
相等
3.在圆、正方形、圆锥、长方体、线段、球、三棱柱、直角三角形中,是立体图形的有 圆锥、长方体、球、三棱柱 ;是平面图形的有 圆、正方形、线段、直角三角形 .
【方法归纳交流】立体图形的各个部分 不在 同一个平面内;平面图形的各个部分 都在 同一个平面内.
圆锥、长方体、球、三棱柱
圆、正方形、线段、直角三角形
不在
都在
直线、射线、线段
4.下列说法正确的是( B )
A.延长射线AD
B.线段AB和线段BA是一条线段
C.连接两点间的线段叫做两点之间的距离
D.若AP=BP,则P是线段AB的中点
B
5.下列各直线的表示方法中,正确的是( D )
A.直线ab B.直线Ab
C.直线A D.直线AB
【方法归纳交流】说说线段、射线、直线的表示方法.
D
线段用表示端点的两个大写字母表示;射线用表示端点和表示射线上另一点的两个大写字母表示(表示端点的字母必须写在前面);直线用表示直线上两个点的两个大写字母表示,也可以用一个小写字母表示.
6.“把弯曲的公路改直,就能缩短路程”,其中蕴含的数学道理是( D )
A.两点确定一条直线 B.直线比曲线短
C.两点之间直线最短 D.两点之间线段最短
7.我们在调整课桌的时候,先确定前后两张课桌,就可以将课桌调齐.其原因是 经过两点有一条直线,并且只有一条直线 .
D
经过两点有一条直线,并且只有一条
直线
8.如图,可以用字母表示出来的不同线段有 10 条.
【变式演练】(1)往返于A、B两个城市的客车,中途有三个停靠点,该客车有 10 种不同的票价,该客车上要准备 20 种车票.
(2)有5个人,每两个人握一次手一共要握 10 次手.
10
10
20
10
对于(2),如果将每个人都看成一点,每两人握一次手可看成连接这两点间的一条线段,则一共可以连接多少条线段?10条.
【方法归纳交流】线段的总条数N与线段上的已知点数n的关系是 N= .
10条.
N=
9.如图,有四点A、B、C、D,按照下列语句画出图形:
(1)画直线AB.
(2)画射线BD.
(3)作线段BC,并以厘米为单位,度量其长度.
(4)线段AC和线段BD相交于点O.
(5)反向延长线段BC至E,使BE=BC.
解:如图,BC=0.7 cm.
尺规作图
10.已知三角形ABC,用直尺和圆规画出一条线段a,使a=AC+BC,然后比较a与AB的长短.(要求:保留作图痕迹,不写作法)
解:如图,a=AC+BC,a>AB.
【方法归纳交流】求作几条线段的和时,先作一条射线,再 顺次 截取即可,线段之和与所画线段的顺序无关.
顺次
11.已知∠1,求作∠AOB,使∠AOB=2∠1.(要求:保留作图痕迹,不写作法)
解:如图,∠AOB即为所求.
线段的有关计算
12.如图,延长线段AB到C,使BC=2AB,取AC的中点D,已知BD=2,求线段AC的长.
解:因为BC=2AB,所以AC=3AB.因为D是AC的中点,所以AD=AC=AB.因为BD=AD-AB,所以2=AB-AB,解得AB=4,所以AC=3×4=12.
13.已知线段AB=24 cm,C是线段AB的中点,D是CB的中点,点E在线段AC上,且CE=AC.画图并计算ED的长.
ED等于哪两条线段的和?这两条线段与已知线段AB有什么数量关系?
ED=EC+CD,EC=AC=AB,CD=AB.
解:如图,因为C是AB的中点,AB=24 cm,所以AC=CB=AB=12 cm.
因为D是CB的中点,所以CD=CB=6 cm.又因为CE=AC=4 cm,所以ED=EC+CD=4+6=10 cm.
因为D是CB的中点,所以CD=CB=6 cm.又因为CE=
AC=4 cm,所以ED=EC+CD=4+6=10 cm.
【方法归纳交流】计算线段的和差时,要结合图形寻找已知线段和所求线段的位置、数量关系,因此 观察图形 是关键.
观察图形
角的计数及计算
14.如图,小于平角的角有( D )
A.5个
B.6个
C.7个
D.8个
D
15.如果∠AOB+∠BOC=90°,且∠BOC与∠COD互余,那么∠AOB与∠COD的关系是( C )
A.互余 B.互补
C.相等 D.不能确定
16.计算:180°-35°43'= 144°17' ;2700″= 45 '= 0.75 °.
C
144°17'
45
0.75
17.(1)从3:15到3:40,时针转过了 12.5 °,分针转过了 150 °.
(2)4:30,时针与分针的夹角为 45 °.
【方法归纳交流】(1)钟表的时针转速为 0.5 °/min,分针转速为 6 °/min.时针(或分针)从某一时刻到另一时刻转过的角度=时针(或分针)转过的 时间 ×时针(或分针)的转速.
12.5
150
45
0.5
6
时间
18.如图,AOB是一条直线,OC是∠AOD的平分线,OE是∠BOD的平分线.
(1)若∠AOE=140°,求∠AOC及∠DOE的度数.
(2)若∠EOD∶∠COD=2∶3,求∠COD及∠BOC的度数.
解:(1)∠DOE=∠BOE=180°-140°=40°;∠AOC=∠AOD=(140°-40°)=50°.
(2)因为OC是∠AOD的平分线,OE是∠BOD的平分线,所以∠COE=∠EOD+∠COD =∠AOB=90°,
所以∠COD=∠AOC=×90°=54°,即∠BOC=180°-∠AOC=126°.
旋转的性质及作图
19.如图,E是正方形ABCD的边CB延长线上一点,把三角形AEB绕着点A逆时针旋转后与三角形AFD重合,则旋转的角度可能是( A )
A
A.90° B.60° C.45° D.30°
20.在下面的网格图中作出三角形ABC以点A为旋转中心按顺时针方向旋转90°后的三角形A1B1C1.
解:如图,三角形A1B1C1即为所求.
角的有关计算
如图,BD平分∠ABC,BE分∠ABC为 2∶5两部分,∠DBE=21°,求∠ABC的度数.
解:设∠ABE=2x,∠CBE=5x,则∠ABC=7x,因为BD平分∠ABC,所以∠ABD=x,又因为∠DBE=∠ABD-∠ABE=x,所以x=21°,解得x=14°,所以∠ABC=98°.
第二章 几何图形的初步认识
第二章 复习课
1.能说出常见的几何体和平面图形的名称,知道点、线、面是构成几何图形的基本元素.
2.能区别线段、射线和直线,明白两点间距离的概念;知道线段、角的表示方法,并会进行度、分、秒的换算;会作一个角等于已知角、作一条线段等于已知线段;知道点与直线的位置关系.
3.知道线段中点及角平分线的含义,并会进行相关的计算.
4.熟记两个基本事实,并能应用它们解决实际问题.
5.知道旋转的概念,熟记旋转的性质.
◎重点:两点间的距离、线段中点、角平分线的概念,线段和角的有关计算.
◎难点:能熟练地进行线段和角的计算,并在实际问题中灵活应用.
请回顾一下,这一章我们都学习了哪些知识?
请你完成本章的知识网络图.
1.请在如图所示的每个几何体下面写出它们的名称.
2.包围着几何体的是 面 ,面与面相交形成 线 ,线与线相交形成 点 .
面
线
点
3.点与直线的位置关系有: 点在直线上(直线经过点) 、 点在直线外(直线不经过点) .
4.两点之间 线段的长度 ,叫做两点之间的距离.
5.有公共 端点 的两条 射线 组成的图形叫做角.
6.如果从一个角的顶点引出的一条 射线 把这个角分成的两个角 相等 ,那么这条 射线 叫做这个角的平分线.
点在直线上(直线经过
点)
点在直线外(直线不经过点)
线段的长度
端点
射线
射线
相等
射线
7.角的度量单位: 度 、 分 、 秒 ,它们之间的关系是:1°= 60 '= 3600 ″;1'= 60 ″;1'= () °;1″= ( '.
度
分
秒
60
3600
60
()
()
8.在平面内,一个图形绕一个 定点 沿某个 方向 转过一个 角度 ,这样的图形运动叫做旋转.这个 定点 叫做旋转中心, 转过的这个角 叫做旋转角.
·导学建议·
预习导学部分可以教师提问学生回答的形式完成,建议学生在课前对不熟悉的知识自己复习,预习导学部分建议教师用10分钟左右的时间完成.
定点
方向
角度
定点
转过的这个角
立体图形与平面图形
1.在圆柱、圆锥、正方体、长方体、棱柱、棱锥、球中,表面有曲面的有 圆柱、圆锥、球 ,只有两个面的有 圆锥 .
圆柱、圆锥、球
圆锥
2.观察下图,回答下列问题.
(1)这个几何体的名称是 六棱柱 .
(2)这个几何体由 6 个侧面, 2 个底面围成,它们分别是 长方 形和 六边 形,这些面都是 平 的.
(3)这个几何体有 18 条棱, 12 个顶点.
六棱柱
6
2
长方
六边
平
18
12
(4)侧面的个数与底面多边形边数的关系是 相等 .
相等
3.在圆、正方形、圆锥、长方体、线段、球、三棱柱、直角三角形中,是立体图形的有 圆锥、长方体、球、三棱柱 ;是平面图形的有 圆、正方形、线段、直角三角形 .
【方法归纳交流】立体图形的各个部分 不在 同一个平面内;平面图形的各个部分 都在 同一个平面内.
圆锥、长方体、球、三棱柱
圆、正方形、线段、直角三角形
不在
都在
直线、射线、线段
4.下列说法正确的是( B )
A.延长射线AD
B.线段AB和线段BA是一条线段
C.连接两点间的线段叫做两点之间的距离
D.若AP=BP,则P是线段AB的中点
B
5.下列各直线的表示方法中,正确的是( D )
A.直线ab B.直线Ab
C.直线A D.直线AB
【方法归纳交流】说说线段、射线、直线的表示方法.
D
线段用表示端点的两个大写字母表示;射线用表示端点和表示射线上另一点的两个大写字母表示(表示端点的字母必须写在前面);直线用表示直线上两个点的两个大写字母表示,也可以用一个小写字母表示.
6.“把弯曲的公路改直,就能缩短路程”,其中蕴含的数学道理是( D )
A.两点确定一条直线 B.直线比曲线短
C.两点之间直线最短 D.两点之间线段最短
7.我们在调整课桌的时候,先确定前后两张课桌,就可以将课桌调齐.其原因是 经过两点有一条直线,并且只有一条直线 .
D
经过两点有一条直线,并且只有一条
直线
8.如图,可以用字母表示出来的不同线段有 10 条.
【变式演练】(1)往返于A、B两个城市的客车,中途有三个停靠点,该客车有 10 种不同的票价,该客车上要准备 20 种车票.
(2)有5个人,每两个人握一次手一共要握 10 次手.
10
10
20
10
对于(2),如果将每个人都看成一点,每两人握一次手可看成连接这两点间的一条线段,则一共可以连接多少条线段?10条.
【方法归纳交流】线段的总条数N与线段上的已知点数n的关系是 N= .
10条.
N=
9.如图,有四点A、B、C、D,按照下列语句画出图形:
(1)画直线AB.
(2)画射线BD.
(3)作线段BC,并以厘米为单位,度量其长度.
(4)线段AC和线段BD相交于点O.
(5)反向延长线段BC至E,使BE=BC.
解:如图,BC=0.7 cm.
尺规作图
10.已知三角形ABC,用直尺和圆规画出一条线段a,使a=AC+BC,然后比较a与AB的长短.(要求:保留作图痕迹,不写作法)
解:如图,a=AC+BC,a>AB.
【方法归纳交流】求作几条线段的和时,先作一条射线,再 顺次 截取即可,线段之和与所画线段的顺序无关.
顺次
11.已知∠1,求作∠AOB,使∠AOB=2∠1.(要求:保留作图痕迹,不写作法)
解:如图,∠AOB即为所求.
线段的有关计算
12.如图,延长线段AB到C,使BC=2AB,取AC的中点D,已知BD=2,求线段AC的长.
解:因为BC=2AB,所以AC=3AB.因为D是AC的中点,所以AD=AC=AB.因为BD=AD-AB,所以2=AB-AB,解得AB=4,所以AC=3×4=12.
13.已知线段AB=24 cm,C是线段AB的中点,D是CB的中点,点E在线段AC上,且CE=AC.画图并计算ED的长.
ED等于哪两条线段的和?这两条线段与已知线段AB有什么数量关系?
ED=EC+CD,EC=AC=AB,CD=AB.
解:如图,因为C是AB的中点,AB=24 cm,所以AC=CB=AB=12 cm.
因为D是CB的中点,所以CD=CB=6 cm.又因为CE=AC=4 cm,所以ED=EC+CD=4+6=10 cm.
因为D是CB的中点,所以CD=CB=6 cm.又因为CE=
AC=4 cm,所以ED=EC+CD=4+6=10 cm.
【方法归纳交流】计算线段的和差时,要结合图形寻找已知线段和所求线段的位置、数量关系,因此 观察图形 是关键.
观察图形
角的计数及计算
14.如图,小于平角的角有( D )
A.5个
B.6个
C.7个
D.8个
D
15.如果∠AOB+∠BOC=90°,且∠BOC与∠COD互余,那么∠AOB与∠COD的关系是( C )
A.互余 B.互补
C.相等 D.不能确定
16.计算:180°-35°43'= 144°17' ;2700″= 45 '= 0.75 °.
C
144°17'
45
0.75
17.(1)从3:15到3:40,时针转过了 12.5 °,分针转过了 150 °.
(2)4:30,时针与分针的夹角为 45 °.
【方法归纳交流】(1)钟表的时针转速为 0.5 °/min,分针转速为 6 °/min.时针(或分针)从某一时刻到另一时刻转过的角度=时针(或分针)转过的 时间 ×时针(或分针)的转速.
12.5
150
45
0.5
6
时间
18.如图,AOB是一条直线,OC是∠AOD的平分线,OE是∠BOD的平分线.
(1)若∠AOE=140°,求∠AOC及∠DOE的度数.
(2)若∠EOD∶∠COD=2∶3,求∠COD及∠BOC的度数.
解:(1)∠DOE=∠BOE=180°-140°=40°;∠AOC=∠AOD=(140°-40°)=50°.
(2)因为OC是∠AOD的平分线,OE是∠BOD的平分线,所以∠COE=∠EOD+∠COD =∠AOB=90°,
所以∠COD=∠AOC=×90°=54°,即∠BOC=180°-∠AOC=126°.
旋转的性质及作图
19.如图,E是正方形ABCD的边CB延长线上一点,把三角形AEB绕着点A逆时针旋转后与三角形AFD重合,则旋转的角度可能是( A )
A
A.90° B.60° C.45° D.30°
20.在下面的网格图中作出三角形ABC以点A为旋转中心按顺时针方向旋转90°后的三角形A1B1C1.
解:如图,三角形A1B1C1即为所求.
角的有关计算
如图,BD平分∠ABC,BE分∠ABC为 2∶5两部分,∠DBE=21°,求∠ABC的度数.
解:设∠ABE=2x,∠CBE=5x,则∠ABC=7x,因为BD平分∠ABC,所以∠ABD=x,又因为∠DBE=∠ABD-∠ABE=x,所以x=21°,解得x=14°,所以∠ABC=98°.
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
