冀教版九年级数学下册 第三十二章投影与视图 复习课课件 (共20张PPT)
文档属性
| 名称 | 冀教版九年级数学下册 第三十二章投影与视图 复习课课件 (共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-27 00:00:00 | ||
图片预览







文档简介
(共20张PPT)
第三十二章 投影与视图
复习课
1.掌握中心投影与平行投影的区别与联系,理解正投影的概念
2.明确三视图的意义,会画简单物体的三视图
3.能够根据三视图还原简单几何体
4.了解直棱柱和圆锥的侧面展开图,并进行简单计算
考点探究
学习目标
课堂总结
知识梳理
考点探究
学习目标
课堂总结
知识梳理
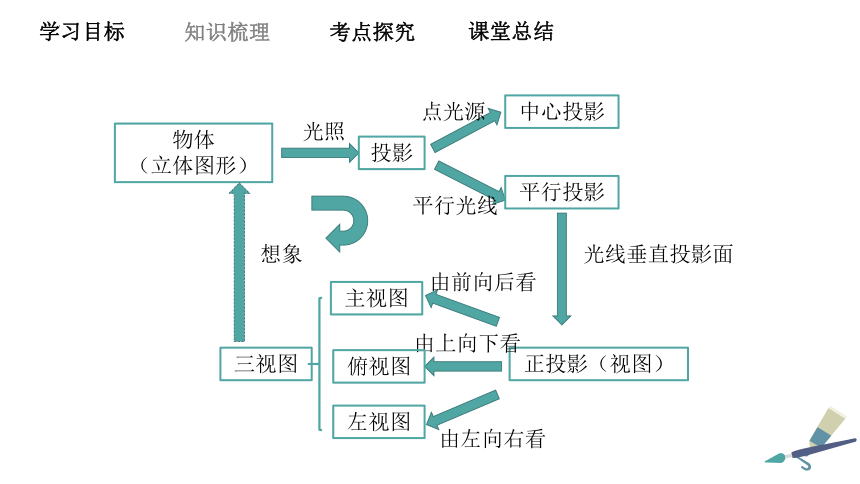
物体
(立体图形)
光照
投影
点光源
平行光线
中心投影
平行投影
光线垂直投影面
正投影(视图)
由前向后看
主视图
由上向下看
俯视图
由左向右看
左视图
三视图
想象
一、平行投影和中心投影
由 形成的投影是平行投影.
由 形成的投影叫做中心投影.
投影线 投影面产生的投影叫做正投影.
平行光线
同一点发出的光线
垂直于
【注意】 (1)在实际制图中,经常采用正投影.
(2)当物体的某个面平行于投影面时,这个面的正投影与这个面的形状、大小完全相同.
(3)阳光下同一时刻不同物体及影长与光线构成的三角形相似.
考点探究
学习目标
课堂总结
知识梳理
二、视图
三视图是 、 、 的统称.
三视图位置有规定:
主视图要在 ,它的下方应是 , 坐落在右边.
三视图的对应规律:主视图和俯视图 ;
主视图和左视图 ;左视图和俯视图 .
【注意】(1)在画图时,看得见部分的轮廓线通常画成实线,看不见部分的轮廓线通常画成虚线.(2)画三视图要认真准确,特别是宽相等.
主视图
俯视图
左视图
左上方
俯视图
左视图
长对正
高平齐
宽相等
考点探究
学习目标
课堂总结
知识梳理
三、直棱柱和圆锥的侧面展开图
考点探究
学习目标
课堂总结
知识梳理
1.直棱柱的侧面展开图是矩形,其面积=直棱柱的底面周长×直棱柱的高.
2.圆锥侧面积公式:S侧=πrl(r为底面圆半径,l为母线长)
3.圆锥全面积公式:S全= (r为底面圆半径,l为母线长)
考点探究
学习目标
课堂总结
知识梳理
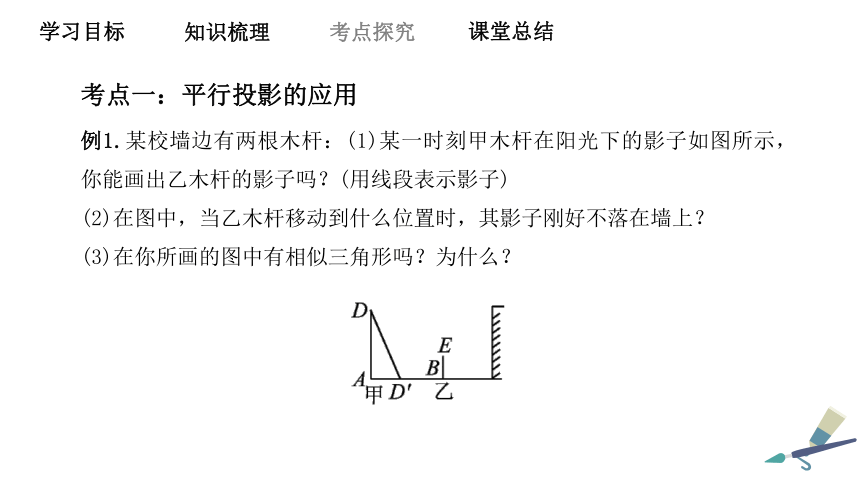
考点一:平行投影的应用
例1.某校墙边有两根木杆:(1)某一时刻甲木杆在阳光下的影子如图所示,你能画出乙木杆的影子吗?(用线段表示影子)
(2)在图中,当乙木杆移动到什么位置时,其影子刚好不落在墙上?
(3)在你所画的图中有相似三角形吗?为什么?
考点探究
学习目标
课堂总结
知识梳理
【解析】所要画出的乙木杆的影子与甲木杆形成的影子是同一时刻,根据同一时刻两物体的高度比等于其影长的比,同时,在同一时刻太阳光线是互相平行的,平行移动乙杆,使乙杆顶端的影长恰好抵达墙角.
解:(1)如图①,过E点作直线DD′的平行线,交AD′所在直线于E′,则BE′为乙木杆的影子.
(2)平移由乙杆、乙杆的影子和太阳光线所构成的图形(即△BEE′),直到其影子的顶端E′抵达墙角(如图②).
(3)△ADD′与△BEE′相似.理由略.
考点探究
学习目标
课堂总结
知识梳理
归纳总结:
由一物体及其影长,画出同一时刻另一物体的影子,其作法是:
(1)过已知物体的顶端及其影长的端点作一直线,再过另一物体的顶端作之前所作的直线的平行线,交已知物体的影子所在直线于一点,则该点到该物体的底部的线段即为影长.但应注意以下两点:①两物体必须在同一平面内;②所求物体的影子必须在已知的影子所在的直线上.
(2)在同一时刻,不同物体的底部中点、顶端的中心及影子的端点所构成的三角形是相似三角形.
考点探究
学习目标
课堂总结
知识梳理
1.如图,下面是北半球一天中四个不同时刻两个建筑物的影子,将它们按时间先后顺序进行排列,正确的是( )
A.③④②① B.②④③① C.③④①② D.③①②④
针对训练
C
考点探究
学习目标
课堂总结
知识梳理
考点二:中心投影的应用
例2.如图,圆桌面(桌面中间有一个直径为0.4m的圆洞)正上方的灯泡(看作一个点)发出的光线照射平行于地面的桌面后,在地面上形成如图所示的圆环形阴影.已知桌面直径为1.2m,桌面离地面1m,若灯泡离地面3m,则地面圆环形阴影的面积是 .
【解析】先根据AC⊥OB,BD⊥OB可得出△AOC∽△BOD,由相似三角形的对应边成比例可求出BD的长,进而得出BD′=0.3m,再由圆环的面积公式即可得出结论.
考点探究
学习目标
课堂总结
知识梳理
解:如图所示:∵AC⊥OB,BD⊥OB,
∴△AOC∽△BOD,
∴ ,即 ,
解得:BD=0.9m,
同理可得:AC′=0.2m,则BD′=0.3m,
∴S圆环形阴影=0.9 π﹣0.3 π=0.72π(m2).
考点探究
学习目标
课堂总结
知识梳理
针对训练
2.如图,王华晚上由路灯A下的B处走到C处时,测得影子CD的长为1 m,继续往前走3 m到达E处时,测得影子EF的长为2 m.已知王华的身高是1.5 m,那么路灯A的高度AB等于( )
A.4.5 m B.6 m C.7.2 m D.8 m
B
考点探究
学习目标
课堂总结
知识梳理
考点三:几何体的三视图
例3.由几何体判断三视图:
如图所示的正六棱柱的主视图是( )
A
考点探究
学习目标
课堂总结
知识梳理
3.如图所示的立体图形的俯视图是( )
针对训练
B
考点探究
学习目标
课堂总结
知识梳理
例4.由三视图还原几何体:
如图所示的三视图所对应的几何体是( )
D
考点探究
学习目标
课堂总结
知识梳理
针对训练
我国古代数学著作《九章算术》中,将底面是直角三角形,且侧棱与底面垂直的三棱柱称为“堑堵”.某“堑堵”的三视图如图所示(网格图中每个小正方形的边长均为1),则该“堑堵”的侧面积为( )
A.
B.
C.
D.
A
考点探究
学习目标
课堂总结
知识梳理
例5.某工厂要加工一批密封罐,设计者给出了密封罐的三视图,请你按照三视图确定制作每个密封罐所需钢板的面积.
分析:对于某些立体图形,沿着其中一些线(例如棱柱的棱)剪开,可以把立体图形的表面展开成一个平面图形——展开图.在实际的生产中,三视图和展开图往往结合在一起使用.解决本题的思路是,由三视图想象出密封罐的立体形状,再进一步画出展开图,从而计算面积.
100
50
50
100
考点四:展开图应用
考点探究
学习目标
课堂总结
知识梳理
解:由三视图可知,密封罐的现状是正六棱柱.
密封罐的高为50mm,底面正六边形的直径为100mm,边长为50mm,图是它的展开图.
由展开图可知,制作一个密封罐所需钢板的面积为
(mm2)
考点探究
学习目标
课堂总结
知识梳理
物体
(立体图形)
光照
投影
点光源
平行光线
中心投影
平行投影
光线垂直投影面
正投影(视图)
由前向后看
主视图
由上向下看
俯视图
由左向右看
左视图
三视图
想象
第三十二章 投影与视图
复习课
1.掌握中心投影与平行投影的区别与联系,理解正投影的概念
2.明确三视图的意义,会画简单物体的三视图
3.能够根据三视图还原简单几何体
4.了解直棱柱和圆锥的侧面展开图,并进行简单计算
考点探究
学习目标
课堂总结
知识梳理
考点探究
学习目标
课堂总结
知识梳理
物体
(立体图形)
光照
投影
点光源
平行光线
中心投影
平行投影
光线垂直投影面
正投影(视图)
由前向后看
主视图
由上向下看
俯视图
由左向右看
左视图
三视图
想象
一、平行投影和中心投影
由 形成的投影是平行投影.
由 形成的投影叫做中心投影.
投影线 投影面产生的投影叫做正投影.
平行光线
同一点发出的光线
垂直于
【注意】 (1)在实际制图中,经常采用正投影.
(2)当物体的某个面平行于投影面时,这个面的正投影与这个面的形状、大小完全相同.
(3)阳光下同一时刻不同物体及影长与光线构成的三角形相似.
考点探究
学习目标
课堂总结
知识梳理
二、视图
三视图是 、 、 的统称.
三视图位置有规定:
主视图要在 ,它的下方应是 , 坐落在右边.
三视图的对应规律:主视图和俯视图 ;
主视图和左视图 ;左视图和俯视图 .
【注意】(1)在画图时,看得见部分的轮廓线通常画成实线,看不见部分的轮廓线通常画成虚线.(2)画三视图要认真准确,特别是宽相等.
主视图
俯视图
左视图
左上方
俯视图
左视图
长对正
高平齐
宽相等
考点探究
学习目标
课堂总结
知识梳理
三、直棱柱和圆锥的侧面展开图
考点探究
学习目标
课堂总结
知识梳理
1.直棱柱的侧面展开图是矩形,其面积=直棱柱的底面周长×直棱柱的高.
2.圆锥侧面积公式:S侧=πrl(r为底面圆半径,l为母线长)
3.圆锥全面积公式:S全= (r为底面圆半径,l为母线长)
考点探究
学习目标
课堂总结
知识梳理
考点一:平行投影的应用
例1.某校墙边有两根木杆:(1)某一时刻甲木杆在阳光下的影子如图所示,你能画出乙木杆的影子吗?(用线段表示影子)
(2)在图中,当乙木杆移动到什么位置时,其影子刚好不落在墙上?
(3)在你所画的图中有相似三角形吗?为什么?
考点探究
学习目标
课堂总结
知识梳理
【解析】所要画出的乙木杆的影子与甲木杆形成的影子是同一时刻,根据同一时刻两物体的高度比等于其影长的比,同时,在同一时刻太阳光线是互相平行的,平行移动乙杆,使乙杆顶端的影长恰好抵达墙角.
解:(1)如图①,过E点作直线DD′的平行线,交AD′所在直线于E′,则BE′为乙木杆的影子.
(2)平移由乙杆、乙杆的影子和太阳光线所构成的图形(即△BEE′),直到其影子的顶端E′抵达墙角(如图②).
(3)△ADD′与△BEE′相似.理由略.
考点探究
学习目标
课堂总结
知识梳理
归纳总结:
由一物体及其影长,画出同一时刻另一物体的影子,其作法是:
(1)过已知物体的顶端及其影长的端点作一直线,再过另一物体的顶端作之前所作的直线的平行线,交已知物体的影子所在直线于一点,则该点到该物体的底部的线段即为影长.但应注意以下两点:①两物体必须在同一平面内;②所求物体的影子必须在已知的影子所在的直线上.
(2)在同一时刻,不同物体的底部中点、顶端的中心及影子的端点所构成的三角形是相似三角形.
考点探究
学习目标
课堂总结
知识梳理
1.如图,下面是北半球一天中四个不同时刻两个建筑物的影子,将它们按时间先后顺序进行排列,正确的是( )
A.③④②① B.②④③① C.③④①② D.③①②④
针对训练
C
考点探究
学习目标
课堂总结
知识梳理
考点二:中心投影的应用
例2.如图,圆桌面(桌面中间有一个直径为0.4m的圆洞)正上方的灯泡(看作一个点)发出的光线照射平行于地面的桌面后,在地面上形成如图所示的圆环形阴影.已知桌面直径为1.2m,桌面离地面1m,若灯泡离地面3m,则地面圆环形阴影的面积是 .
【解析】先根据AC⊥OB,BD⊥OB可得出△AOC∽△BOD,由相似三角形的对应边成比例可求出BD的长,进而得出BD′=0.3m,再由圆环的面积公式即可得出结论.
考点探究
学习目标
课堂总结
知识梳理
解:如图所示:∵AC⊥OB,BD⊥OB,
∴△AOC∽△BOD,
∴ ,即 ,
解得:BD=0.9m,
同理可得:AC′=0.2m,则BD′=0.3m,
∴S圆环形阴影=0.9 π﹣0.3 π=0.72π(m2).
考点探究
学习目标
课堂总结
知识梳理
针对训练
2.如图,王华晚上由路灯A下的B处走到C处时,测得影子CD的长为1 m,继续往前走3 m到达E处时,测得影子EF的长为2 m.已知王华的身高是1.5 m,那么路灯A的高度AB等于( )
A.4.5 m B.6 m C.7.2 m D.8 m
B
考点探究
学习目标
课堂总结
知识梳理
考点三:几何体的三视图
例3.由几何体判断三视图:
如图所示的正六棱柱的主视图是( )
A
考点探究
学习目标
课堂总结
知识梳理
3.如图所示的立体图形的俯视图是( )
针对训练
B
考点探究
学习目标
课堂总结
知识梳理
例4.由三视图还原几何体:
如图所示的三视图所对应的几何体是( )
D
考点探究
学习目标
课堂总结
知识梳理
针对训练
我国古代数学著作《九章算术》中,将底面是直角三角形,且侧棱与底面垂直的三棱柱称为“堑堵”.某“堑堵”的三视图如图所示(网格图中每个小正方形的边长均为1),则该“堑堵”的侧面积为( )
A.
B.
C.
D.
A
考点探究
学习目标
课堂总结
知识梳理
例5.某工厂要加工一批密封罐,设计者给出了密封罐的三视图,请你按照三视图确定制作每个密封罐所需钢板的面积.
分析:对于某些立体图形,沿着其中一些线(例如棱柱的棱)剪开,可以把立体图形的表面展开成一个平面图形——展开图.在实际的生产中,三视图和展开图往往结合在一起使用.解决本题的思路是,由三视图想象出密封罐的立体形状,再进一步画出展开图,从而计算面积.
100
50
50
100
考点四:展开图应用
考点探究
学习目标
课堂总结
知识梳理
解:由三视图可知,密封罐的现状是正六棱柱.
密封罐的高为50mm,底面正六边形的直径为100mm,边长为50mm,图是它的展开图.
由展开图可知,制作一个密封罐所需钢板的面积为
(mm2)
考点探究
学习目标
课堂总结
知识梳理
物体
(立体图形)
光照
投影
点光源
平行光线
中心投影
平行投影
光线垂直投影面
正投影(视图)
由前向后看
主视图
由上向下看
俯视图
由左向右看
左视图
三视图
想象
