冀教版七年级上册数学 第四章 整式的加减 复习课 课件(共25张PPT)
文档属性
| 名称 | 冀教版七年级上册数学 第四章 整式的加减 复习课 课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 965.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-27 18:30:01 | ||
图片预览








文档简介
(共25张PPT)
第四章 整式的加减
第四章 复习课
1.能根据概念正确辨析单项式、多项式、整式,能正确指出单项式的系数、次数,多项式的次数、项等.
2.知道合并同类项的法则和去括号的法则,并能熟练运用这些法则进行整式加减的计算,并能求代数式的值.
3.能用整式加减解决一些简单的实际问题.
◎重点:单项式、多项式、整式、同类项等概念.
◎难点:去括号法则、合并同类项的方法.
老师宣布游戏规则:请你任选一个数,先乘3再减6,结果乘以2,最后加上12.只要你说出最后的结果,老师就能马上说出当初你所选择的数.请学生计算后说出自己的结果,老师迅速说出学生所选的数,激发学生的兴趣.
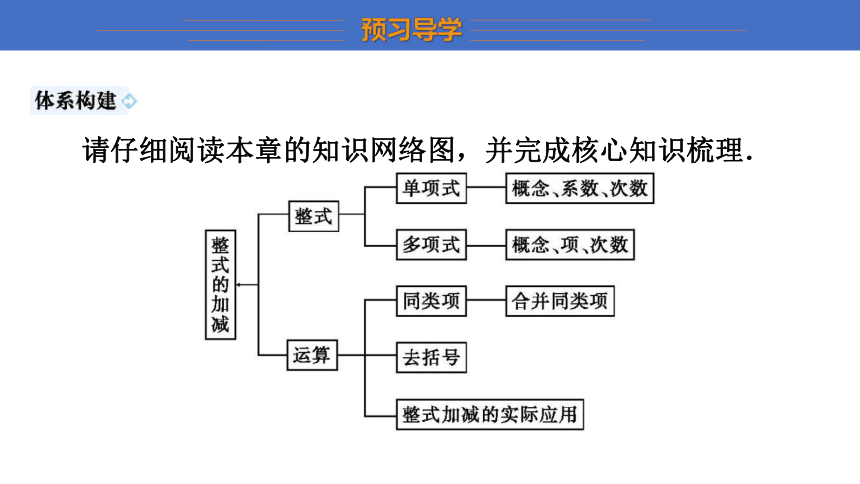
请仔细阅读本章的知识网络图,并完成核心知识梳理.
1.整式包括 单项式 和 多项式 .
2.单项式中数字和字母(或字母和字母)是 相乘 关系,多项式是单项式的 和 .
3.单项式中的 数字因数 叫做单项式的系数, 所有字母 的指数的和叫做单项式的次数.
单项式
多项式
相乘
和
数字因数
所有字
母
4.多项式中每一个 单项式 叫做多项式的项, 不含字母 的项叫做常数项; 最高次项 的次数叫做多项式的次数.
5.在多项式中, 所含字母 相同,相同字母的指数也相同的项叫做同类项;在合并同类项时,把同类项的系数 相加 ,字母和字母的指数 不变 .
单项式
不含字
母
最高次项
所含字母
相
加
不变
6.去括号法则:①括号前是“+”时,把括号和它前面的“+”去掉,原括号里的各项都 不改变 符号;②括号前是“-”时,把括号和它前面的“-”去掉,原括号里的各项都 改变 符号.
·导学建议·
预习导学部分可以让学生独立完成,并请中等水平的学生到黑板上板演.
不改变
改变
单项式、多项式、整式等概念
1.下列说法正确的是( C )
A.的系数是 B.x2y没有系数
C.x+2不是单项式 D.0不是单项式
C
2.将代数式-mn,x,,-a4b,,8,-y,,1+a,mn-8ab,4x2-4x+1,进行分类,其中单项式有 -mn,x,-a4b,8,-y, ,多项式有 ,1+a,mn-8ab,4x2-4x+1 ,整式有 -mn,x,-a4b,8,-y,, ,1+a,mn-8ab,4x2-4x+1 .
-
mn,x,-a4b,8,-y,
,1+a,mn-
8ab,4x2-4x+1
-mn,x,-a4b,8,-y,
, ,1+a,mn-8ab,4x2-4x+1
3.含有字母x、y且系数为2的四次单项式总共有 3 个.
3
4.已知多项式3xn+1-(m-2)x2+2是关于x的三次二项式,求mn-4的值.
解:因为3xn+1-(m-2)x2+2是关于x的三次二项式,
所以n+1=3,m-2=0,解得n=2,m=2,
所以mn-4=22-4=0.
【方法归纳交流】在对代数式进行分类时,要注意分母中含有 字母 的既不是单项式,也不是多项式.
字母
·导学建议·
概念是数学学习的重要组成部分,这部分的题目不但要求学生会做,还要让学生能够运用“概念”说清理由,从而夯实基础.
同类项
5.若M=2a2b,N=3ab2,P=-4a2b,则下列各式中正确的是( C )
A.M+N=5a3b3 B.N+P=-ab
C.M+P=-2a2b D.M-P=2a2b
C
6.下列各式中,是同类项的是 ③⑤ .(填序号)
①2x2y3与x3y2,②ab2c和ab2,③-xy和yx,④(-a)3和(-3)3,⑤0和π.
③⑤
7.若2a3+mb5-pa4bn+1=-7a4b5,则m+n-p= -4 .
-4
·导学建议·
关于式的运算归根结底就是合并同类项,而合并同类项的前提是能够正确识别同类项,所以对于同类项的识别要让学生抓好“两个相同”和“两个无关”.
【方法归纳交流】(1)几个单项式能够合并成一项,说明它们是 同类项 ;(2)特殊地,几个常数项 是 (填“是”或“不是”)同类项,其中π是 数字 不是 字母 .
同类项
是
数字
字母
去括号的法则
8.下列选项中,去括号所得结果正确的是( B )
A.x2-2(x-y+2z)=x2-2x+2y+2z
B.x-(-2x+3y-1)=x+2x-3y+1
C.3x-=3x-5x-x+1
D.(x-1)-3(x2-2)=x-1-3x2-6
B
9.如图,已知有理数a,b在数轴上的位置,化简代数式:++.
解:原式=-(a-b)+(b-a)-(a+b)=-3a+b.
【方法归纳交流】化简带绝对值符号的代数式时,关键是去掉 绝对值符号 .去掉绝对值符号的方法是:若a>0,则= a ;若a=0,则= 0 ;若a<0,则= -a .要注意给去掉绝对值符号的代数式加 括号 .
绝对值符号
a
0
-
a
括号
第9题与数轴、绝对值的知识相结合,体现了数学知识的综合运用.对于部分学生会有一定的难度,教学过程中要注重观察学生,并适时地进行引导.
·导学建议·
整式的加减及其应用
10.使(ax2-2xy+y2)-(-ax2+bxy+2y2)=6x2-9xy+cy2成立的a,b,c依次是( C )
A.3,-7,-1 B.-3,7,-1
C.3,7,-1 D.-3,7,1
C
11.若A=3x2-2x-5,B=2x2-2x-7,则A与B的大小关系是( A )
A.A>B B.A<B
C.A=B D.无法确定
A
12.已知第一个多项式A=x2-xy+y2,第二个多项式是第一个多项式的3倍减2,第三个多项式是第一个多项式与第二个多项式的差,求这三个多项式的和.
解:三个多项式的和为A+(3A-2)+=A+3A-2+A-3A+2=2A,
因为A=x2-xy+y2,
所以这三个多项式的和为2A=2(x2-xy+y2)=2x2-2xy+2y2.
【方法归纳交流】多项式参加运算时,我们把多项式看成一个 整体 ,所以要注意给多项式加上 括号 后再进行运算.
整体
括号
代数式求值中的整体思想
已知x-y=2,y+z=3,求多项式(x-y)2+(x+z)2-(y+z)2的值.
解:因为(x-y)+(y+z)=2+3=5,所以(x-y)+(y+z)=x+z=5,
把x-y=2,y+z=3,x+z=5代入多项式,得原式=22+52-32=20.
【方法归纳交流】当不能求出代数式中所含字母的具体值时,一般采用整体代入法求值.
·导学建议·
利用整式加减化简求值是一项重要的应用,而学生刚刚接触,先化简再求值的意识可能会比较薄弱,所以要加强这方面的培养.例如,在第12题中,会有相当一部分学生会列出很复杂的式子,增加了计算难度,要利用学生的错误,通过两种解题方法的比较,让学生树立化简意识.
第四章 整式的加减
第四章 复习课
1.能根据概念正确辨析单项式、多项式、整式,能正确指出单项式的系数、次数,多项式的次数、项等.
2.知道合并同类项的法则和去括号的法则,并能熟练运用这些法则进行整式加减的计算,并能求代数式的值.
3.能用整式加减解决一些简单的实际问题.
◎重点:单项式、多项式、整式、同类项等概念.
◎难点:去括号法则、合并同类项的方法.
老师宣布游戏规则:请你任选一个数,先乘3再减6,结果乘以2,最后加上12.只要你说出最后的结果,老师就能马上说出当初你所选择的数.请学生计算后说出自己的结果,老师迅速说出学生所选的数,激发学生的兴趣.
请仔细阅读本章的知识网络图,并完成核心知识梳理.
1.整式包括 单项式 和 多项式 .
2.单项式中数字和字母(或字母和字母)是 相乘 关系,多项式是单项式的 和 .
3.单项式中的 数字因数 叫做单项式的系数, 所有字母 的指数的和叫做单项式的次数.
单项式
多项式
相乘
和
数字因数
所有字
母
4.多项式中每一个 单项式 叫做多项式的项, 不含字母 的项叫做常数项; 最高次项 的次数叫做多项式的次数.
5.在多项式中, 所含字母 相同,相同字母的指数也相同的项叫做同类项;在合并同类项时,把同类项的系数 相加 ,字母和字母的指数 不变 .
单项式
不含字
母
最高次项
所含字母
相
加
不变
6.去括号法则:①括号前是“+”时,把括号和它前面的“+”去掉,原括号里的各项都 不改变 符号;②括号前是“-”时,把括号和它前面的“-”去掉,原括号里的各项都 改变 符号.
·导学建议·
预习导学部分可以让学生独立完成,并请中等水平的学生到黑板上板演.
不改变
改变
单项式、多项式、整式等概念
1.下列说法正确的是( C )
A.的系数是 B.x2y没有系数
C.x+2不是单项式 D.0不是单项式
C
2.将代数式-mn,x,,-a4b,,8,-y,,1+a,mn-8ab,4x2-4x+1,进行分类,其中单项式有 -mn,x,-a4b,8,-y, ,多项式有 ,1+a,mn-8ab,4x2-4x+1 ,整式有 -mn,x,-a4b,8,-y,, ,1+a,mn-8ab,4x2-4x+1 .
-
mn,x,-a4b,8,-y,
,1+a,mn-
8ab,4x2-4x+1
-mn,x,-a4b,8,-y,
, ,1+a,mn-8ab,4x2-4x+1
3.含有字母x、y且系数为2的四次单项式总共有 3 个.
3
4.已知多项式3xn+1-(m-2)x2+2是关于x的三次二项式,求mn-4的值.
解:因为3xn+1-(m-2)x2+2是关于x的三次二项式,
所以n+1=3,m-2=0,解得n=2,m=2,
所以mn-4=22-4=0.
【方法归纳交流】在对代数式进行分类时,要注意分母中含有 字母 的既不是单项式,也不是多项式.
字母
·导学建议·
概念是数学学习的重要组成部分,这部分的题目不但要求学生会做,还要让学生能够运用“概念”说清理由,从而夯实基础.
同类项
5.若M=2a2b,N=3ab2,P=-4a2b,则下列各式中正确的是( C )
A.M+N=5a3b3 B.N+P=-ab
C.M+P=-2a2b D.M-P=2a2b
C
6.下列各式中,是同类项的是 ③⑤ .(填序号)
①2x2y3与x3y2,②ab2c和ab2,③-xy和yx,④(-a)3和(-3)3,⑤0和π.
③⑤
7.若2a3+mb5-pa4bn+1=-7a4b5,则m+n-p= -4 .
-4
·导学建议·
关于式的运算归根结底就是合并同类项,而合并同类项的前提是能够正确识别同类项,所以对于同类项的识别要让学生抓好“两个相同”和“两个无关”.
【方法归纳交流】(1)几个单项式能够合并成一项,说明它们是 同类项 ;(2)特殊地,几个常数项 是 (填“是”或“不是”)同类项,其中π是 数字 不是 字母 .
同类项
是
数字
字母
去括号的法则
8.下列选项中,去括号所得结果正确的是( B )
A.x2-2(x-y+2z)=x2-2x+2y+2z
B.x-(-2x+3y-1)=x+2x-3y+1
C.3x-=3x-5x-x+1
D.(x-1)-3(x2-2)=x-1-3x2-6
B
9.如图,已知有理数a,b在数轴上的位置,化简代数式:++.
解:原式=-(a-b)+(b-a)-(a+b)=-3a+b.
【方法归纳交流】化简带绝对值符号的代数式时,关键是去掉 绝对值符号 .去掉绝对值符号的方法是:若a>0,则= a ;若a=0,则= 0 ;若a<0,则= -a .要注意给去掉绝对值符号的代数式加 括号 .
绝对值符号
a
0
-
a
括号
第9题与数轴、绝对值的知识相结合,体现了数学知识的综合运用.对于部分学生会有一定的难度,教学过程中要注重观察学生,并适时地进行引导.
·导学建议·
整式的加减及其应用
10.使(ax2-2xy+y2)-(-ax2+bxy+2y2)=6x2-9xy+cy2成立的a,b,c依次是( C )
A.3,-7,-1 B.-3,7,-1
C.3,7,-1 D.-3,7,1
C
11.若A=3x2-2x-5,B=2x2-2x-7,则A与B的大小关系是( A )
A.A>B B.A<B
C.A=B D.无法确定
A
12.已知第一个多项式A=x2-xy+y2,第二个多项式是第一个多项式的3倍减2,第三个多项式是第一个多项式与第二个多项式的差,求这三个多项式的和.
解:三个多项式的和为A+(3A-2)+=A+3A-2+A-3A+2=2A,
因为A=x2-xy+y2,
所以这三个多项式的和为2A=2(x2-xy+y2)=2x2-2xy+2y2.
【方法归纳交流】多项式参加运算时,我们把多项式看成一个 整体 ,所以要注意给多项式加上 括号 后再进行运算.
整体
括号
代数式求值中的整体思想
已知x-y=2,y+z=3,求多项式(x-y)2+(x+z)2-(y+z)2的值.
解:因为(x-y)+(y+z)=2+3=5,所以(x-y)+(y+z)=x+z=5,
把x-y=2,y+z=3,x+z=5代入多项式,得原式=22+52-32=20.
【方法归纳交流】当不能求出代数式中所含字母的具体值时,一般采用整体代入法求值.
·导学建议·
利用整式加减化简求值是一项重要的应用,而学生刚刚接触,先化简再求值的意识可能会比较薄弱,所以要加强这方面的培养.例如,在第12题中,会有相当一部分学生会列出很复杂的式子,增加了计算难度,要利用学生的错误,通过两种解题方法的比较,让学生树立化简意识.
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
