华东师大版八年级数学上册14.2 勾股定理的应用 第1课时最短路径问题 课件 (共23张PPT)
文档属性
| 名称 | 华东师大版八年级数学上册14.2 勾股定理的应用 第1课时最短路径问题 课件 (共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 36.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-27 18:31:02 | ||
图片预览


文档简介
(共23张PPT)
华东师大版八年级(上)
一1从2勾服定壁的应用
第1课时最短路径问题
复习回顾
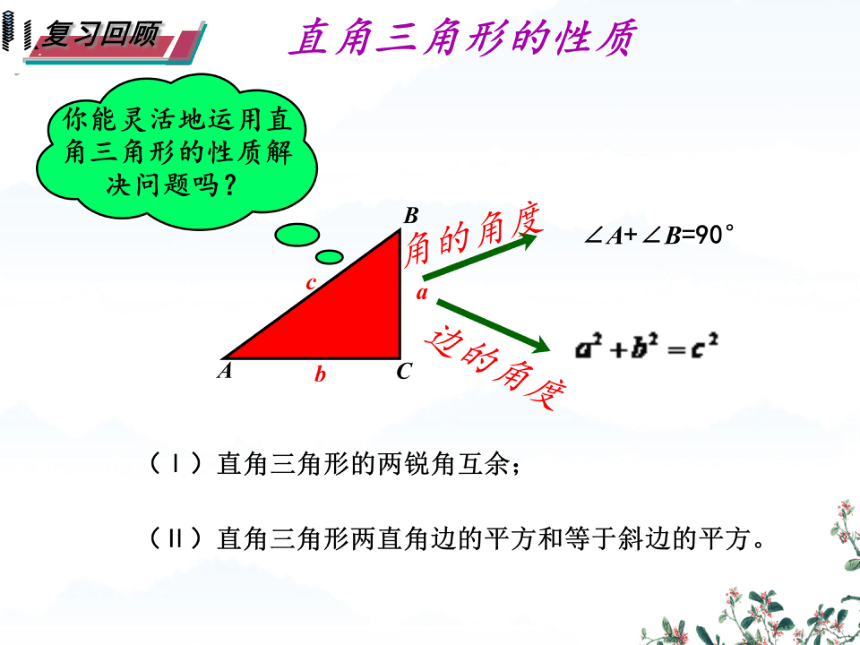
直角三角形的性质
你能灵活地运用直
角三角形的性质解
决问题吗?
角的角度
∠A+∠B=90°
A
b
边的角度
2+b2=c2
(丨)直角三角形的两锐角互余;
(川)直角三角形两直角边的平方和等于斜边的平方。
复习回顾
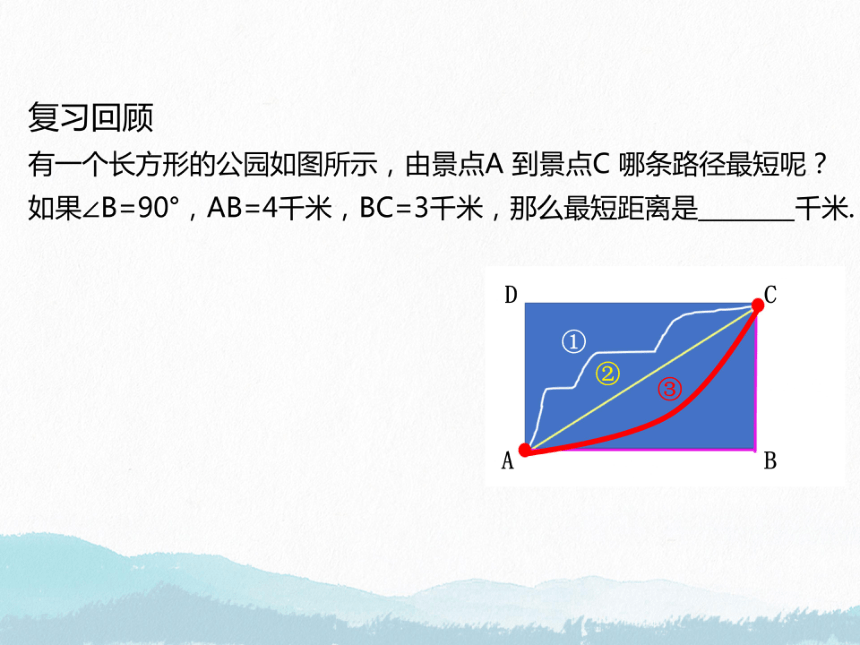
有一个长方形的公园如图所示,由景点A到景点C哪条路径最短呢?
如果∠B=90°,AB=4干米,BC=3干米,那么最短距离是
干米
D
①
②
⑧
A
B
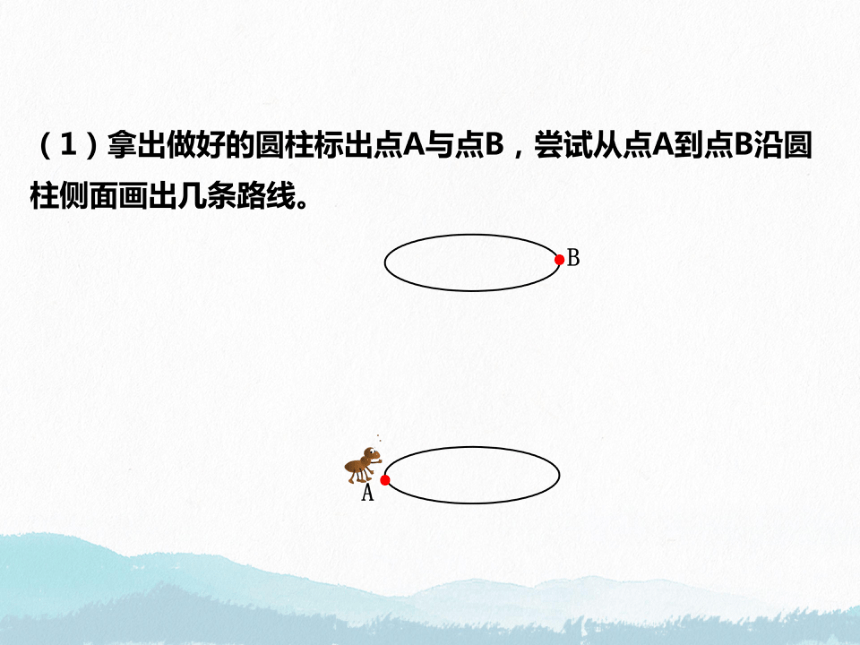
(1)拿出做好的圆柱标出点A与点B,尝试从点A到点B沿圆
柱侧面画出几条路线。
B
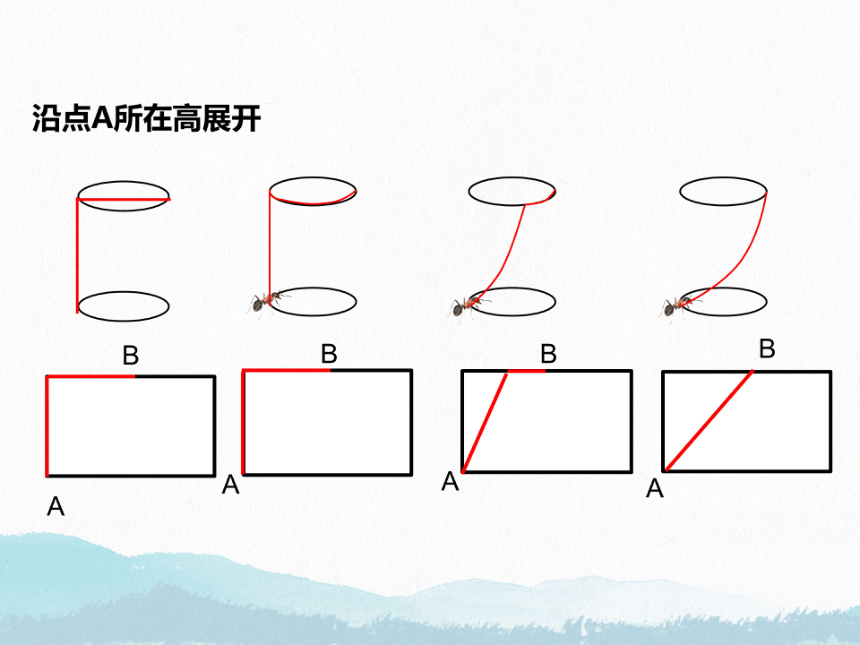
沿点A所在高展开
B
B
B
B
A
A
A
A
情境导入
最短路径问题
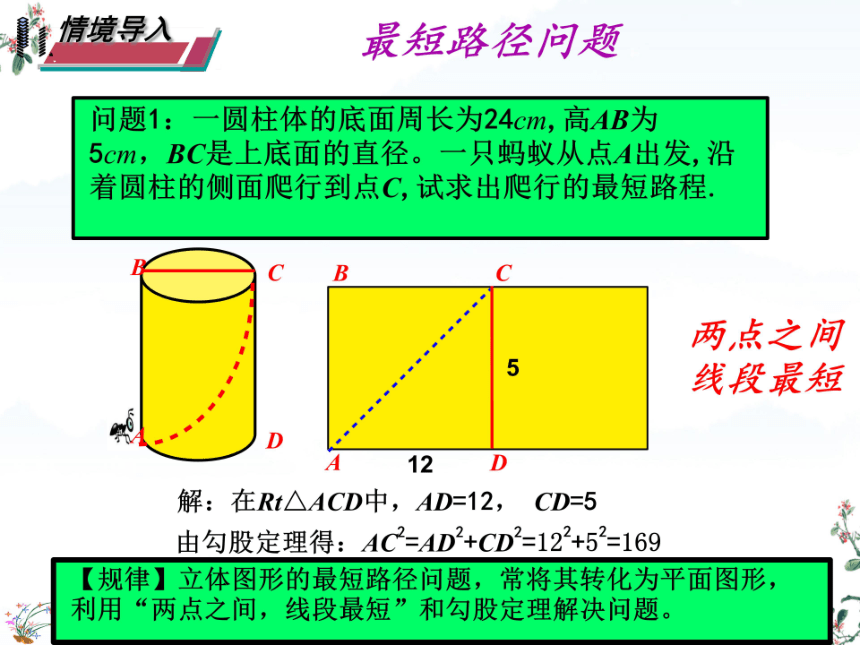
问题1:一圆柱体的底面周长为24cm,高AB为
5cm,BC是上底面的直径。一只蚂蚁从点A出发,沿
着圆柱的侧面爬行到点C,试求出爬行的最短路程,
B
两点之间
线段最短
12
解:在Rt△ACD中,AD=12,
CD-5
由勾股定理得:AC2=AD2+CD2=122+52=169
【规律】立体图形的最短路径问题,常将其转化为平面图形,
利用“两点之间,线段最短”和勾股定理解决问题
探究发现
最短路径问题
变式1:
一
圆柱体的底面周长为24cm,高AB为5cm,
BC
是上底面的直径。一只蚂蚁从点A出发,沿着圆柱的
侧面爬行到蜘蛛相对的圆柱体的上口外侧距开口1cm
的点E,试求出爬行的最短路程。
B
12
AD2+DE=AE
探究发现
最短路径问题
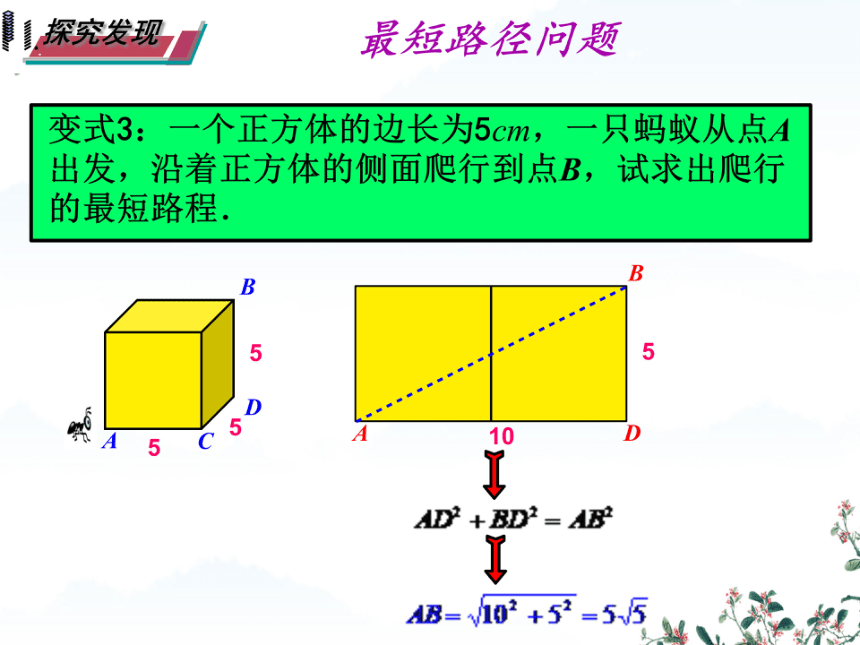
变式3:一个正方体的边长为5cm,一只蚂蚁从点A
出发,沿着正方体的侧面爬行到点B,试求出爬行
的最短路程.
B
B
5
5
D
5
5
10
D2+8D产=B
Y
dB=V102+52=55
探究发现
最短路径问题
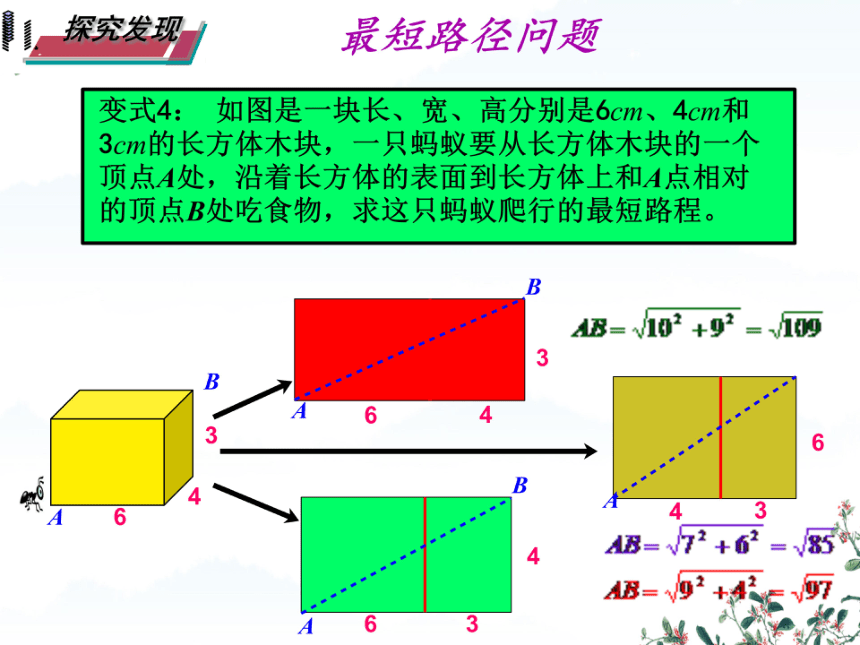
变式4:如图是一块长、宽、高分别是6cm、4cm和
3cm的长方体木块,一只蚂蚁要从长方体木块的一个
顶点A处,沿着长方体的表面到长方体上和A点相对
的顶点B处吃食物,求这只蚂蚁爬行的最短路程。
B
B=102+g2=1则
3
4
6
B
3
0
AB=72+62=85
4
AB-
6
3
探究发现
最短路径问题
结论
解决立体图形的最短路径问题,常常将其转化为平面图
形,利用“两点之间,线段最短”和勾股定理解决问题。
简记
展→连,一算
探究新知2
一辆装满货物的卡车,其外形高2.5米,宽1.6
米,要开进厂门形状如图14.2.3所示的某工
B
厂,问这辆卡车能否通过该工厂的厂门(厂门
上方为半圆形拱门)?
解
在Rt△OCD中,由勾股定理,可得
米
CD=√0C2-0D=√2-0.82=0.6,
CH=CD+DH=0.6+2.3=2.9>2.5.
0.8米
2米
可见高度上有0.4米的余量,因此卡车能通过厂门
华东师大版八年级(上)
一1从2勾服定壁的应用
第1课时最短路径问题
复习回顾
直角三角形的性质
你能灵活地运用直
角三角形的性质解
决问题吗?
角的角度
∠A+∠B=90°
A
b
边的角度
2+b2=c2
(丨)直角三角形的两锐角互余;
(川)直角三角形两直角边的平方和等于斜边的平方。
复习回顾
有一个长方形的公园如图所示,由景点A到景点C哪条路径最短呢?
如果∠B=90°,AB=4干米,BC=3干米,那么最短距离是
干米
D
①
②
⑧
A
B
(1)拿出做好的圆柱标出点A与点B,尝试从点A到点B沿圆
柱侧面画出几条路线。
B
沿点A所在高展开
B
B
B
B
A
A
A
A
情境导入
最短路径问题
问题1:一圆柱体的底面周长为24cm,高AB为
5cm,BC是上底面的直径。一只蚂蚁从点A出发,沿
着圆柱的侧面爬行到点C,试求出爬行的最短路程,
B
两点之间
线段最短
12
解:在Rt△ACD中,AD=12,
CD-5
由勾股定理得:AC2=AD2+CD2=122+52=169
【规律】立体图形的最短路径问题,常将其转化为平面图形,
利用“两点之间,线段最短”和勾股定理解决问题
探究发现
最短路径问题
变式1:
一
圆柱体的底面周长为24cm,高AB为5cm,
BC
是上底面的直径。一只蚂蚁从点A出发,沿着圆柱的
侧面爬行到蜘蛛相对的圆柱体的上口外侧距开口1cm
的点E,试求出爬行的最短路程。
B
12
AD2+DE=AE
探究发现
最短路径问题
变式3:一个正方体的边长为5cm,一只蚂蚁从点A
出发,沿着正方体的侧面爬行到点B,试求出爬行
的最短路程.
B
B
5
5
D
5
5
10
D2+8D产=B
Y
dB=V102+52=55
探究发现
最短路径问题
变式4:如图是一块长、宽、高分别是6cm、4cm和
3cm的长方体木块,一只蚂蚁要从长方体木块的一个
顶点A处,沿着长方体的表面到长方体上和A点相对
的顶点B处吃食物,求这只蚂蚁爬行的最短路程。
B
B=102+g2=1则
3
4
6
B
3
0
AB=72+62=85
4
AB-
6
3
探究发现
最短路径问题
结论
解决立体图形的最短路径问题,常常将其转化为平面图
形,利用“两点之间,线段最短”和勾股定理解决问题。
简记
展→连,一算
探究新知2
一辆装满货物的卡车,其外形高2.5米,宽1.6
米,要开进厂门形状如图14.2.3所示的某工
B
厂,问这辆卡车能否通过该工厂的厂门(厂门
上方为半圆形拱门)?
解
在Rt△OCD中,由勾股定理,可得
米
CD=√0C2-0D=√2-0.82=0.6,
CH=CD+DH=0.6+2.3=2.9>2.5.
0.8米
2米
可见高度上有0.4米的余量,因此卡车能通过厂门
