4.5一次函数的应用 课件(共63张PPT) 2023-2024学年湘教版数学八年级下册
文档属性
| 名称 | 4.5一次函数的应用 课件(共63张PPT) 2023-2024学年湘教版数学八年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-27 00:00:00 | ||
图片预览










文档简介
(共63张PPT)
4.5 一次函数的应用
第1课时 利用一次函数解决实际问题
湘教版数学八年级下册
第4章 一次函数
复习回顾
1.一次函数的表达式为:
y=kx+b(k≠0)
2.待定系数法求一次函数表达式的步骤:
(1)设出一次函数表达式:
y=kx+b(k≠0)
(2)利用给定两点建立二元一次方程组:
(3)解二元一次方程组,得k和b的值,代入表达式即可.
某地为保护环境,鼓励节约用电,实行阶梯电价制度. 规定每户居民每月用电量不超过160kW·h,则按0.6元/(kW·h)收费;若超过160kW·h,则超出部分每1kW·h加收0.1元.
(1)写出某户居民某月应缴纳的电费y(元)与用电量x(kW·h)之间的函数表达式;
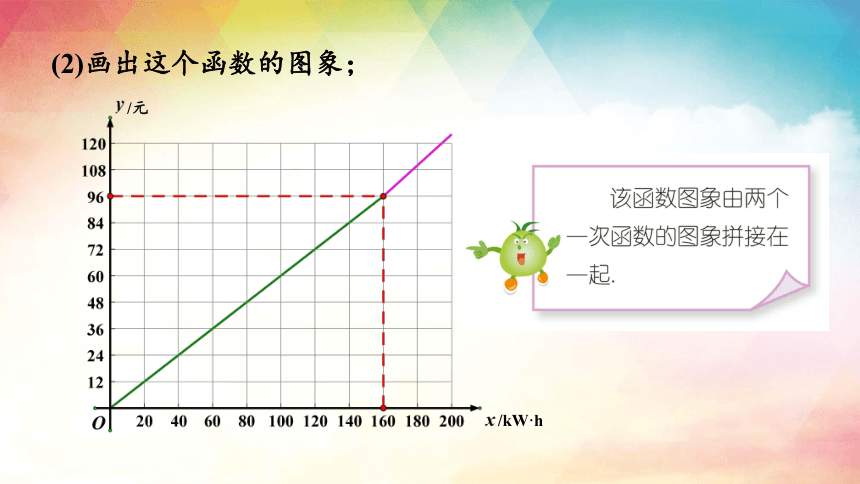
(2)画出这个函数的图象;
(3)小王家3月份,4月份分别用电150kW·h和200kW·h,应缴纳电费各多少元?
探索新知
(1)写出某户居民某月应缴纳的电费y(元)与用电量x(kW·h)之间的函数表达式;
解:电费与用电量相关.
当0≤x≤160时,y=0.6x;
当x>160时, y=160×0.6+(x-160)×(0.6+0.1)=0.7x-16.
y与x的函数表达式也可以合起来表示为
(2)画出这个函数的图象;
/元
/kW·h
(3)小王家3月份,4月份分别用电150kW·h和200kW·h,应缴纳电费各多少元?
当x=150时,y=0.6×150=90,即3月份的电费为90元.
当x=200时,y=0.7×200-16=124,即4月份的电费为124元.
甲、乙两地相距40km,小明8:00点骑自行车由甲地去乙地,平均车速为8km/h;小红10:00坐公共汽车也由甲地去乙地,平均车速为40km/h.设小明所用的时间为x(h),小明与甲地的距离为y1(km),小红离甲地的距离为y2(km).
(1)分别写出y1,y2与x之间的函数表达式;
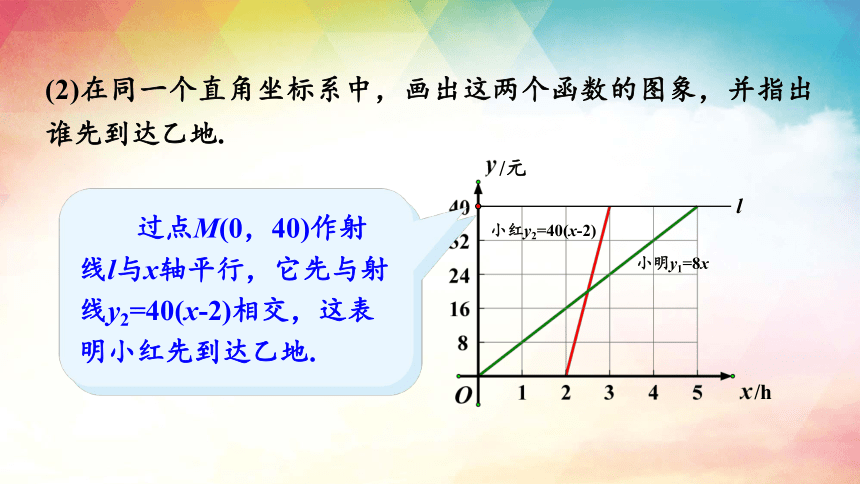
(2)在同一个直角坐标系中,画出这两个函数的图象,并指出谁先到达乙地.
【教材P134页】
(1)分别写出y1,y2与x之间的函数表达式;
解:小明所用时间为xh,由“路程=速度×时间”可知y1= 8x,自变量x的取值范围是0≤x≤5.
由于小红比小明晚出发2h,因此小红所用时间为(x-2)h.
从而 y2=40(x-2),
自变量x的取值范围是2≤x≤3.
(2)在同一个直角坐标系中,画出这两个函数的图象,并指出谁先到达乙地.
/元
/h
l
小明y1=8x
小红y2=40(x-2)
过点M(0,40)作射线l与x轴平行,它先与射线y2=40(x-2)相交,这表明小红先到达乙地.
练习
为全面推进乡村振兴,拓宽农民增收致富渠道,某村通过种植优质荔枝新品种,实现荔枝品牌化发展,助推村民增收致富.该村张师傅驾车运送荔枝到某地出售,汽车出发前油箱有油 50 L,行驶若干小时后,途中在加油站加油若干升,油箱中剩余油量y(L)与行驶时间 t(h) 之间的关系如图所示.
【教材P134页】
(1)汽车行驶_____h后加油,中途加油_____L.
(2)求加油前油箱剩余油量 y 与行驶时间 t 的函数关系式.
为全面推进乡村振兴,拓宽农民增收致富渠道,某村通过种植优质荔枝新品种,实现荔枝品牌化发展,助推村民增收致富.该村张师傅驾车运送荔枝到某地出售,汽车出发前油箱有油 50 L,行驶若干小时后,途中在加油站加油若干升,油箱中剩余油量y(L)与行驶时间 t(h) 之间的关系如图所示.
为全面推进乡村振兴,拓宽农民增收致富渠道,某村通过种植优质荔枝新品种,实现荔枝品牌化发展,助推村民增收致富.该村张师傅驾车运送荔枝到某地出售,汽车出发前油箱有油 50 L,行驶若干小时后,途中在加油站加油若干升,油箱中剩余油量y(L)与行驶时间 t(h) 之间的关系如图所示.
(3)已知加油前、后汽车都以70 km/h 匀速行驶,如果加油站距目的地210 km,要到达目的地,问油箱中的油是否够用 请说明理由.
随堂练习
1.如图,l1反映某公司产品的销售收入与销售量的关系,l2反映该公司产品的销售成本与销售量的关系,根据图象判断该公司盈利时的销售量( )
A.小于4件 B.大于4件
C.等于4件 D.大于或等于4件
B
2.甲、乙两名运动员进行长跑训练,两人距终点的路程y(米)与长跑时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答问题:
(1)他们在进行______米的长跑训练,在0(2)求甲距终点的路程y(米)和跑步时间t(分)之间的函数关系式;
(3)当x=15时,两人相距多少米?在155000
甲
(2)解:设一次函数的表达式为y=kx+b,
由于点A(0, 5000),B(20, 0)都在一次函数图像上,将这两点坐标带入表达式,得
k·0 + b = 5000,
k·20 + b = 0.
解得k=-250,b=5000.
因此所求一次函数的解析式为y=-250x+5000
(3)解:当x=15时,由图象可知乙距离终点2000m,
甲距离终点-250×15+5000=1250m.
两人相距2000-1250=750(m).
在15一次函数的应用
对分段函数图像的理解及运用
建立一次函数模型解决实际问题
课堂小结
课堂小结
1. 说一说本节课的收获。
2. 你还存在哪些疑惑?
4.5 一次函数的应用
第2课时 建立一次函数模型解决预测类型的实际问题
湘教版数学八年级下册
第4章 一次函数
情境导入
王大强和张小勇两人比赛跑步,路程和时间的关系如图:根据图象回答下列问题:
(1)王大强和张小勇谁跑的快?
王大强:100÷18≈5.56(m/s).
张小勇:80÷18≈4.44(m/s).
5.56>4.44,故王大强跑得快.
王大强和张小勇两人比赛跑步,路程和时间的关系如图:根据图象回答下列问题:
(2)出发几秒后两人相遇?
(3)相遇前谁在前面?相遇后谁在前面?
由图可知,出发18s后两人相遇.
情境导入
由图可知,相遇前张小勇在前面,相遇后王大强在前面.
情境导入
王大强和张小勇两人比赛跑步,路程和时间的关系如图:根据图象回答下列问题:
(4)你还能读出什么信息?
对于利用一次函数的图象解决问题,我们比较熟练,如果给出表格的形式来解决一次函数的问题,你会做吗?
探索新知
奥运会早期,男子撑杆跳高的纪录如下表所示:
观察这个表中第二行的数据,你能为奥运会的撑杆跳高纪录与奥运年份的关系建立函数模型吗?
上表中每一届比上一届的纪录提高了0.2m,可以试着建立一次函数的模型.
用t表示从1900年起增加的年份,则在奥运会早期,男子撑杆跳高的纪录y(m)与t的函数关系式可以设为
y=kx+b
由于t=0(即1900年)时,撑杆跳高的纪录为3.33m;t=4(即1904年)时,纪录为3.53m,因此
解得b=3.33,k=0.05. 于是y=0.05t+3.33.
当t=8时,y=3.73,这说明1908年的撑杆跳高纪录也符合公式①.
公式①就是奥运会早期男子撑杆跳高纪录y与时间t之间的函数表达式.
能利用公式预测1912年奥运会的男子撑杆跳高纪录吗?
y=0.05×12+3.33=3.93
实际上,1912年奥运会男子撑杆跳高纪录约为3.93m.这表明用所建立的函数模型,在已知数据邻近做预测,结果与实际情况比较吻合.
能够利用公式预测20 世纪80年代,譬如1988年奥运会男子撑杆跳高纪录吗?
y=0.05×88+3.33=7.73
然而,1988年奥运会的男子撑杆跳高纪录是5.90m, 远低于7.73m. 这表明用所建立的函数模型远离已知数据做预测是不可靠的.
总结归纳
通过建立函数模型,对变量的变化情况进行预测问题的解题步骤:
1.分析数据,找出自变量和因变量,发现对应关系;
2.抽象出函数表达式;
3.将验证并化简函数表达式,得出问题的变化规律.
请每位同学伸出一只手掌,把大拇指与小拇指尽量张开, 两指间的距离称为指距. 已知指距与身高具有如下关系:
(1)求身高y与指距x之间的函数表达式;
(2)当李华的指距为22cm时,你能预测他的身高吗?
【教材P136页】
(1)解:上表3组数据反映了身高y与指距x之间的对应关系,观察这两个变量之间的变化规律,当指距增加1cm,身高就增加9cm,可以建立一次函数模型.
设身高y与指距x之间的函数表达式为y=kx+b.将x=19, y=151与x=20,y=160代入上式,得
19k + b = 151,
20k + b = 160.
解得k=9,b=-20.
于是y=9x-20. ①
将x=21,y=169代入①式也符合.
公式①就是身高y与指距x之间的函数表达式.
(2)解:当x=22时,y=9×22-20=178.
因此,李华的身高大约是178cm.
练习
1. 在某地,人们发现某种蟋蟀1min所叫次数与当地气温之间近似为一次函数关系. 下面是蟋蟀所叫次数与气温变化情况对照表:
(1)根据表中数据确定该一次函数的表达式;
【教材P137页】
解:设蟋蟀1min所叫次数与气温之间的函数表达式为y=kx+b.
将x=15,y=84与x=20,y=119代入上式,得
15k + b = 84,
20k + b = 119.
解得k=7,b=-21. 于是y=7x-21.
当x=17时,y=17×7-21=98,这说明温度在17℃时,叫声次数符合公式y=7x-21.
(2) 如果蟋蟀1min叫了63次,那么该地当时的气温大约为多少摄氏度?
解:当y=63时,有y=7x-21=63,解得x=12.
(3) 能用所求出的函数模型来预测蟋蟀在0 ℃时所鸣叫的次数吗?
解:不能,因为此函数关系是近似的,与实际生活中的情况有所不符,蟋蟀在0℃时可能不会鸣叫.而且根据公式,x=0时,y=-21,这是不可能的,故不能模拟.
2.某商店今年7月初销售纯净水的数量如下表所示:
(1)你能为销售纯净水的数量与时间之间的关系建立函数模型吗?
(2)用所求出的函数解析式预测今年7月5日该商店销售纯净水的数量.
【教材P137页】
(1)你能为销售纯净水的数量与时间之间的关系建立函数模型吗?
解:设销售纯净水的数量与时间之间的函数表达式为y=kx+b.
将x=1,y=160与x=2,y=165代入上式,得
k + b = 160,
2k + b = 165.
解得k=5,b=155. 于是y=5x+155.
当x=3时,y=3×5+155=170,符合公式y=5x+155.
(2)用所求出的函数解析式预测今年7月5日该商店销售纯净水的数量.
解:当x=5时,y=5×5+155=180.因此,今年7月5日该商店销售纯净水的数量为180瓶.
随堂练习
1. 如图所示,某公司市场营销部的营销人员的个人收入与其每月的销售量成一次函数关系,由图中给出的信息,营销人员没有销售量时的收入是( )
A.310元 B.300元
C.290元 D.280元
B
2.出版社出版适合中学生阅读的科普读物,该读物首次出版印刷的印数不少于5000册时,投入的成本与印数间的相应数据如下:
印数x(册) 5000 8000 10000 15000
成本y(元) 28500 36000 41000 53500
(1)通过对上表的数据的探究,发现该种读数的投入成本y与印数x之间是一次函数,则此函数的解析式为___________(不写自变量的取值范围);
y=2.5x+16000
2.出版社出版适合中学生阅读的科普读物,该读物首次出版印刷的印数不少于5000册时,投入的成本与印数间的相应数据如下:
印数x(册) 5000 8000 10000 15000
成本y(元) 28500 36000 41000 53500
(2)如果出片社投入成本48000元,那么能印该读物______
________册.
128000
2.鞋的“鞋码”和鞋长(cm)存在一种换算关系,下表是几组“鞋码”与鞋长换算的对应数值:
鞋长(cm) 16 19 21 24
鞋码(号) 22 28 32 38
(1)设鞋长为x,“鞋码”为y,试判断点(x,y)在你学过的哪种函数的图象上?
(2)求x、y之间的函数关系式;
(3)如果某人穿44号“鞋码”的鞋,那么他的鞋长是多少?
[注:“鞋码”是表示鞋子大小的一种号码]
一次函数
y=2x-10
44=2x-10,x=27
课堂小结
一次函数模型的应用
①将实验得到的数据在直角坐标系中描出
②观察这些点的特征,确定选用的函数形式,并根据已知数据求出具体的函数表达式
③进行检验
④应用这个函数模型解决问题
4.5 一次函数的应用
第3课时 一次函数与一次方程的联系
湘教版数学八年级下册
第4章 一次函数
探索新知
一次函数y=5-x的图象如图所示.
(1)方程x+y=5的解有多少个?写出其中的几个.
(2)在直角坐标系中分别描出以这些解为坐标的点,它们在一次函数y=5-x的图象上吗?
(3)在一次函数y=5-x的图象上任取一点,它的坐标满足方程x+y=5吗?
(4)以方程x+y=5的解为坐标的所有点组成的图象与一次函数y=5-x的图象相同吗?
我们知道二元一次方程x+y=5的解有无数组,以这些解为坐标的点在一次函数y=5-x的图象上. 将方程x+y=5化成一次函数的形式:y=5-x,易知该一次函数的图象上任意一点的坐标也满足方程x+y=5.
事实上,以二元一次方程x+y=5的解为坐标的点所组成的图形与一次函数y=5-x的图象完全相同.
总结归纳
一般地,一次函数y=kx+b图象上任意一点的坐标都是二元一次方程kx-y+b=0的一个解,以二元一次方程kx-y+b=0的解为坐标的点都在一次函数y=kx+b的图象上.
你能找到下面两个问题之间的联系吗?
(1)解方程:3x-6=0.
(2)已知一次函数y=3x-6,问x取何值时,y=0?
(1)方程3x-6=0的解为x=2.
(2)画出函数y=3x-6的图象.
从图中可以看出,一次函数y=3x-6的图象与x轴交于点(2,0),这就是当y=0时,得x=2,而x=2正是方程3x-6=0的解.
总结归纳
一般地,一次函数y=kx+b(k≠0)的图象与x轴的交点的横坐标是一元一次方程kx+b=0的解.任何一个一元一次方程kx+b=0的解,就是一次函数y=kx+b的图象与x轴交点的横坐标.
已知一次函数y=2x+6,求这个函数的图象与x轴交点的横坐标.
解法一:
解:令y=0,解方程2x+6=0,得
x=-3.
所以一次函数y=2x+6的图象与x轴交点的横坐标为-3.
【教材P138页】
解法二:
解:画出函数y=2x+6的图象(如图所示),直线y=2x+6与x轴交于点(-3,0),所以该图象与x轴交点的横坐标为-3.
y=2x+6
已知一次函数y=2x+6,求这个函数的图象与x轴交点的横坐标.
【教材P138页】
这两种解法分别从“数”与“形”的角度出发来解决问题.
练习
1.把下列二元一次方程改写成y=kx+b的形式.
(1)3x+y=7; (2)3x+4y=13.
解:y=-3x+7
解:y=
【教材P139页】
2.已知函数y=3x+9,自变量满足什么条件时,y=0?
解:画出函数y=3x+9的图象(如图所示),直线y=3x+9与x轴交于点(-3,0),所以x=-3时y=0.
y=3x+9
【教材P139页】
3.利用函数图象,解方程3x-9=0.
解:画出函数y=3x+9的图象,如图所示,
y=3x-9
直线y=3x-9与x轴交于点(3,0),
所以方程3x-9=0 的解为x=3.
【教材P139页】
随堂练习
1.若直线y=kx+b的图象经过点(1,3),则方程kx+b=3的解是( )
A. x=1 B. x=2 C. x=3 D. x=4
A
2.下列图象中,以方程y-2x-2=0的解为坐标的点组成的图象是( )
C
3.直线y=3x+6与x轴交点的横坐标的值是方程2x+m=0的解,则m的值是________.
4.已知函数y=kx+b的图象如图所示:
(1)求k、b的值;
(2)在图中画出函数y=-2x+5的图象,并根据图象回答:当x取何值时,函数y=kx+b的函数值等于函数y=-2x+5的函数值.
4
(1)解:设一次函数的表达式为y=kx+b,
由于点(-2, 0),Q(0, 2)都在一次函数图像上,将这两点坐标带入表达式,得
-2k + b = 0,
b = 2.
解得k=1,b=2.
(2)解:画出函数y=x+2与y=-2x+5的图象,当x=1时,两函数值相等.
y=x+2
y=-2x+5
课堂小结
1.一般地,一次函数y=kx+b图象上任意一点的坐标都是二元一次方程kx-y+b=0的一个解,以二元一次方程kx-y+b=0的解为坐标的点都在一次函数y=kx+b的图象上.
2.一般地,一次函数y=kx+b(k≠0)的图象与x轴的交点的横坐标是一元一次方程kx+b=0的解.任何一个一元一次方程kx+b=0的解,就是一次函数y=kx+b的图象与x轴交点的横坐标.
3.从“数”与“形”的角度出发来解决问题.
谢谢观看
4.5 一次函数的应用
第1课时 利用一次函数解决实际问题
湘教版数学八年级下册
第4章 一次函数
复习回顾
1.一次函数的表达式为:
y=kx+b(k≠0)
2.待定系数法求一次函数表达式的步骤:
(1)设出一次函数表达式:
y=kx+b(k≠0)
(2)利用给定两点建立二元一次方程组:
(3)解二元一次方程组,得k和b的值,代入表达式即可.
某地为保护环境,鼓励节约用电,实行阶梯电价制度. 规定每户居民每月用电量不超过160kW·h,则按0.6元/(kW·h)收费;若超过160kW·h,则超出部分每1kW·h加收0.1元.
(1)写出某户居民某月应缴纳的电费y(元)与用电量x(kW·h)之间的函数表达式;
(2)画出这个函数的图象;
(3)小王家3月份,4月份分别用电150kW·h和200kW·h,应缴纳电费各多少元?
探索新知
(1)写出某户居民某月应缴纳的电费y(元)与用电量x(kW·h)之间的函数表达式;
解:电费与用电量相关.
当0≤x≤160时,y=0.6x;
当x>160时, y=160×0.6+(x-160)×(0.6+0.1)=0.7x-16.
y与x的函数表达式也可以合起来表示为
(2)画出这个函数的图象;
/元
/kW·h
(3)小王家3月份,4月份分别用电150kW·h和200kW·h,应缴纳电费各多少元?
当x=150时,y=0.6×150=90,即3月份的电费为90元.
当x=200时,y=0.7×200-16=124,即4月份的电费为124元.
甲、乙两地相距40km,小明8:00点骑自行车由甲地去乙地,平均车速为8km/h;小红10:00坐公共汽车也由甲地去乙地,平均车速为40km/h.设小明所用的时间为x(h),小明与甲地的距离为y1(km),小红离甲地的距离为y2(km).
(1)分别写出y1,y2与x之间的函数表达式;
(2)在同一个直角坐标系中,画出这两个函数的图象,并指出谁先到达乙地.
【教材P134页】
(1)分别写出y1,y2与x之间的函数表达式;
解:小明所用时间为xh,由“路程=速度×时间”可知y1= 8x,自变量x的取值范围是0≤x≤5.
由于小红比小明晚出发2h,因此小红所用时间为(x-2)h.
从而 y2=40(x-2),
自变量x的取值范围是2≤x≤3.
(2)在同一个直角坐标系中,画出这两个函数的图象,并指出谁先到达乙地.
/元
/h
l
小明y1=8x
小红y2=40(x-2)
过点M(0,40)作射线l与x轴平行,它先与射线y2=40(x-2)相交,这表明小红先到达乙地.
练习
为全面推进乡村振兴,拓宽农民增收致富渠道,某村通过种植优质荔枝新品种,实现荔枝品牌化发展,助推村民增收致富.该村张师傅驾车运送荔枝到某地出售,汽车出发前油箱有油 50 L,行驶若干小时后,途中在加油站加油若干升,油箱中剩余油量y(L)与行驶时间 t(h) 之间的关系如图所示.
【教材P134页】
(1)汽车行驶_____h后加油,中途加油_____L.
(2)求加油前油箱剩余油量 y 与行驶时间 t 的函数关系式.
为全面推进乡村振兴,拓宽农民增收致富渠道,某村通过种植优质荔枝新品种,实现荔枝品牌化发展,助推村民增收致富.该村张师傅驾车运送荔枝到某地出售,汽车出发前油箱有油 50 L,行驶若干小时后,途中在加油站加油若干升,油箱中剩余油量y(L)与行驶时间 t(h) 之间的关系如图所示.
为全面推进乡村振兴,拓宽农民增收致富渠道,某村通过种植优质荔枝新品种,实现荔枝品牌化发展,助推村民增收致富.该村张师傅驾车运送荔枝到某地出售,汽车出发前油箱有油 50 L,行驶若干小时后,途中在加油站加油若干升,油箱中剩余油量y(L)与行驶时间 t(h) 之间的关系如图所示.
(3)已知加油前、后汽车都以70 km/h 匀速行驶,如果加油站距目的地210 km,要到达目的地,问油箱中的油是否够用 请说明理由.
随堂练习
1.如图,l1反映某公司产品的销售收入与销售量的关系,l2反映该公司产品的销售成本与销售量的关系,根据图象判断该公司盈利时的销售量( )
A.小于4件 B.大于4件
C.等于4件 D.大于或等于4件
B
2.甲、乙两名运动员进行长跑训练,两人距终点的路程y(米)与长跑时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答问题:
(1)他们在进行______米的长跑训练,在0
(3)当x=15时,两人相距多少米?在15
甲
(2)解:设一次函数的表达式为y=kx+b,
由于点A(0, 5000),B(20, 0)都在一次函数图像上,将这两点坐标带入表达式,得
k·0 + b = 5000,
k·20 + b = 0.
解得k=-250,b=5000.
因此所求一次函数的解析式为y=-250x+5000
(3)解:当x=15时,由图象可知乙距离终点2000m,
甲距离终点-250×15+5000=1250m.
两人相距2000-1250=750(m).
在15
对分段函数图像的理解及运用
建立一次函数模型解决实际问题
课堂小结
课堂小结
1. 说一说本节课的收获。
2. 你还存在哪些疑惑?
4.5 一次函数的应用
第2课时 建立一次函数模型解决预测类型的实际问题
湘教版数学八年级下册
第4章 一次函数
情境导入
王大强和张小勇两人比赛跑步,路程和时间的关系如图:根据图象回答下列问题:
(1)王大强和张小勇谁跑的快?
王大强:100÷18≈5.56(m/s).
张小勇:80÷18≈4.44(m/s).
5.56>4.44,故王大强跑得快.
王大强和张小勇两人比赛跑步,路程和时间的关系如图:根据图象回答下列问题:
(2)出发几秒后两人相遇?
(3)相遇前谁在前面?相遇后谁在前面?
由图可知,出发18s后两人相遇.
情境导入
由图可知,相遇前张小勇在前面,相遇后王大强在前面.
情境导入
王大强和张小勇两人比赛跑步,路程和时间的关系如图:根据图象回答下列问题:
(4)你还能读出什么信息?
对于利用一次函数的图象解决问题,我们比较熟练,如果给出表格的形式来解决一次函数的问题,你会做吗?
探索新知
奥运会早期,男子撑杆跳高的纪录如下表所示:
观察这个表中第二行的数据,你能为奥运会的撑杆跳高纪录与奥运年份的关系建立函数模型吗?
上表中每一届比上一届的纪录提高了0.2m,可以试着建立一次函数的模型.
用t表示从1900年起增加的年份,则在奥运会早期,男子撑杆跳高的纪录y(m)与t的函数关系式可以设为
y=kx+b
由于t=0(即1900年)时,撑杆跳高的纪录为3.33m;t=4(即1904年)时,纪录为3.53m,因此
解得b=3.33,k=0.05. 于是y=0.05t+3.33.
当t=8时,y=3.73,这说明1908年的撑杆跳高纪录也符合公式①.
公式①就是奥运会早期男子撑杆跳高纪录y与时间t之间的函数表达式.
能利用公式预测1912年奥运会的男子撑杆跳高纪录吗?
y=0.05×12+3.33=3.93
实际上,1912年奥运会男子撑杆跳高纪录约为3.93m.这表明用所建立的函数模型,在已知数据邻近做预测,结果与实际情况比较吻合.
能够利用公式预测20 世纪80年代,譬如1988年奥运会男子撑杆跳高纪录吗?
y=0.05×88+3.33=7.73
然而,1988年奥运会的男子撑杆跳高纪录是5.90m, 远低于7.73m. 这表明用所建立的函数模型远离已知数据做预测是不可靠的.
总结归纳
通过建立函数模型,对变量的变化情况进行预测问题的解题步骤:
1.分析数据,找出自变量和因变量,发现对应关系;
2.抽象出函数表达式;
3.将验证并化简函数表达式,得出问题的变化规律.
请每位同学伸出一只手掌,把大拇指与小拇指尽量张开, 两指间的距离称为指距. 已知指距与身高具有如下关系:
(1)求身高y与指距x之间的函数表达式;
(2)当李华的指距为22cm时,你能预测他的身高吗?
【教材P136页】
(1)解:上表3组数据反映了身高y与指距x之间的对应关系,观察这两个变量之间的变化规律,当指距增加1cm,身高就增加9cm,可以建立一次函数模型.
设身高y与指距x之间的函数表达式为y=kx+b.将x=19, y=151与x=20,y=160代入上式,得
19k + b = 151,
20k + b = 160.
解得k=9,b=-20.
于是y=9x-20. ①
将x=21,y=169代入①式也符合.
公式①就是身高y与指距x之间的函数表达式.
(2)解:当x=22时,y=9×22-20=178.
因此,李华的身高大约是178cm.
练习
1. 在某地,人们发现某种蟋蟀1min所叫次数与当地气温之间近似为一次函数关系. 下面是蟋蟀所叫次数与气温变化情况对照表:
(1)根据表中数据确定该一次函数的表达式;
【教材P137页】
解:设蟋蟀1min所叫次数与气温之间的函数表达式为y=kx+b.
将x=15,y=84与x=20,y=119代入上式,得
15k + b = 84,
20k + b = 119.
解得k=7,b=-21. 于是y=7x-21.
当x=17时,y=17×7-21=98,这说明温度在17℃时,叫声次数符合公式y=7x-21.
(2) 如果蟋蟀1min叫了63次,那么该地当时的气温大约为多少摄氏度?
解:当y=63时,有y=7x-21=63,解得x=12.
(3) 能用所求出的函数模型来预测蟋蟀在0 ℃时所鸣叫的次数吗?
解:不能,因为此函数关系是近似的,与实际生活中的情况有所不符,蟋蟀在0℃时可能不会鸣叫.而且根据公式,x=0时,y=-21,这是不可能的,故不能模拟.
2.某商店今年7月初销售纯净水的数量如下表所示:
(1)你能为销售纯净水的数量与时间之间的关系建立函数模型吗?
(2)用所求出的函数解析式预测今年7月5日该商店销售纯净水的数量.
【教材P137页】
(1)你能为销售纯净水的数量与时间之间的关系建立函数模型吗?
解:设销售纯净水的数量与时间之间的函数表达式为y=kx+b.
将x=1,y=160与x=2,y=165代入上式,得
k + b = 160,
2k + b = 165.
解得k=5,b=155. 于是y=5x+155.
当x=3时,y=3×5+155=170,符合公式y=5x+155.
(2)用所求出的函数解析式预测今年7月5日该商店销售纯净水的数量.
解:当x=5时,y=5×5+155=180.因此,今年7月5日该商店销售纯净水的数量为180瓶.
随堂练习
1. 如图所示,某公司市场营销部的营销人员的个人收入与其每月的销售量成一次函数关系,由图中给出的信息,营销人员没有销售量时的收入是( )
A.310元 B.300元
C.290元 D.280元
B
2.出版社出版适合中学生阅读的科普读物,该读物首次出版印刷的印数不少于5000册时,投入的成本与印数间的相应数据如下:
印数x(册) 5000 8000 10000 15000
成本y(元) 28500 36000 41000 53500
(1)通过对上表的数据的探究,发现该种读数的投入成本y与印数x之间是一次函数,则此函数的解析式为___________(不写自变量的取值范围);
y=2.5x+16000
2.出版社出版适合中学生阅读的科普读物,该读物首次出版印刷的印数不少于5000册时,投入的成本与印数间的相应数据如下:
印数x(册) 5000 8000 10000 15000
成本y(元) 28500 36000 41000 53500
(2)如果出片社投入成本48000元,那么能印该读物______
________册.
128000
2.鞋的“鞋码”和鞋长(cm)存在一种换算关系,下表是几组“鞋码”与鞋长换算的对应数值:
鞋长(cm) 16 19 21 24
鞋码(号) 22 28 32 38
(1)设鞋长为x,“鞋码”为y,试判断点(x,y)在你学过的哪种函数的图象上?
(2)求x、y之间的函数关系式;
(3)如果某人穿44号“鞋码”的鞋,那么他的鞋长是多少?
[注:“鞋码”是表示鞋子大小的一种号码]
一次函数
y=2x-10
44=2x-10,x=27
课堂小结
一次函数模型的应用
①将实验得到的数据在直角坐标系中描出
②观察这些点的特征,确定选用的函数形式,并根据已知数据求出具体的函数表达式
③进行检验
④应用这个函数模型解决问题
4.5 一次函数的应用
第3课时 一次函数与一次方程的联系
湘教版数学八年级下册
第4章 一次函数
探索新知
一次函数y=5-x的图象如图所示.
(1)方程x+y=5的解有多少个?写出其中的几个.
(2)在直角坐标系中分别描出以这些解为坐标的点,它们在一次函数y=5-x的图象上吗?
(3)在一次函数y=5-x的图象上任取一点,它的坐标满足方程x+y=5吗?
(4)以方程x+y=5的解为坐标的所有点组成的图象与一次函数y=5-x的图象相同吗?
我们知道二元一次方程x+y=5的解有无数组,以这些解为坐标的点在一次函数y=5-x的图象上. 将方程x+y=5化成一次函数的形式:y=5-x,易知该一次函数的图象上任意一点的坐标也满足方程x+y=5.
事实上,以二元一次方程x+y=5的解为坐标的点所组成的图形与一次函数y=5-x的图象完全相同.
总结归纳
一般地,一次函数y=kx+b图象上任意一点的坐标都是二元一次方程kx-y+b=0的一个解,以二元一次方程kx-y+b=0的解为坐标的点都在一次函数y=kx+b的图象上.
你能找到下面两个问题之间的联系吗?
(1)解方程:3x-6=0.
(2)已知一次函数y=3x-6,问x取何值时,y=0?
(1)方程3x-6=0的解为x=2.
(2)画出函数y=3x-6的图象.
从图中可以看出,一次函数y=3x-6的图象与x轴交于点(2,0),这就是当y=0时,得x=2,而x=2正是方程3x-6=0的解.
总结归纳
一般地,一次函数y=kx+b(k≠0)的图象与x轴的交点的横坐标是一元一次方程kx+b=0的解.任何一个一元一次方程kx+b=0的解,就是一次函数y=kx+b的图象与x轴交点的横坐标.
已知一次函数y=2x+6,求这个函数的图象与x轴交点的横坐标.
解法一:
解:令y=0,解方程2x+6=0,得
x=-3.
所以一次函数y=2x+6的图象与x轴交点的横坐标为-3.
【教材P138页】
解法二:
解:画出函数y=2x+6的图象(如图所示),直线y=2x+6与x轴交于点(-3,0),所以该图象与x轴交点的横坐标为-3.
y=2x+6
已知一次函数y=2x+6,求这个函数的图象与x轴交点的横坐标.
【教材P138页】
这两种解法分别从“数”与“形”的角度出发来解决问题.
练习
1.把下列二元一次方程改写成y=kx+b的形式.
(1)3x+y=7; (2)3x+4y=13.
解:y=-3x+7
解:y=
【教材P139页】
2.已知函数y=3x+9,自变量满足什么条件时,y=0?
解:画出函数y=3x+9的图象(如图所示),直线y=3x+9与x轴交于点(-3,0),所以x=-3时y=0.
y=3x+9
【教材P139页】
3.利用函数图象,解方程3x-9=0.
解:画出函数y=3x+9的图象,如图所示,
y=3x-9
直线y=3x-9与x轴交于点(3,0),
所以方程3x-9=0 的解为x=3.
【教材P139页】
随堂练习
1.若直线y=kx+b的图象经过点(1,3),则方程kx+b=3的解是( )
A. x=1 B. x=2 C. x=3 D. x=4
A
2.下列图象中,以方程y-2x-2=0的解为坐标的点组成的图象是( )
C
3.直线y=3x+6与x轴交点的横坐标的值是方程2x+m=0的解,则m的值是________.
4.已知函数y=kx+b的图象如图所示:
(1)求k、b的值;
(2)在图中画出函数y=-2x+5的图象,并根据图象回答:当x取何值时,函数y=kx+b的函数值等于函数y=-2x+5的函数值.
4
(1)解:设一次函数的表达式为y=kx+b,
由于点(-2, 0),Q(0, 2)都在一次函数图像上,将这两点坐标带入表达式,得
-2k + b = 0,
b = 2.
解得k=1,b=2.
(2)解:画出函数y=x+2与y=-2x+5的图象,当x=1时,两函数值相等.
y=x+2
y=-2x+5
课堂小结
1.一般地,一次函数y=kx+b图象上任意一点的坐标都是二元一次方程kx-y+b=0的一个解,以二元一次方程kx-y+b=0的解为坐标的点都在一次函数y=kx+b的图象上.
2.一般地,一次函数y=kx+b(k≠0)的图象与x轴的交点的横坐标是一元一次方程kx+b=0的解.任何一个一元一次方程kx+b=0的解,就是一次函数y=kx+b的图象与x轴交点的横坐标.
3.从“数”与“形”的角度出发来解决问题.
谢谢观看
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
