物理人教版(2019)选择性必修第一册1.5弹性碰撞和非弹性碰撞(共15张ppt)
文档属性
| 名称 | 物理人教版(2019)选择性必修第一册1.5弹性碰撞和非弹性碰撞(共15张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 40.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-12-27 21:10:07 | ||
图片预览






文档简介
(共15张PPT)
第一章 动量守恒定律
第5节 弹性碰撞与非弹性碰撞
新教材人教版 物理(高中选择性必修第一册)
新课引入
课堂引入
思考与讨论:
2.实验时,为什么将球叠放在一起,最上面的球就能被弹到很高的位置?
1.小球被弹的很高,说明小球具有的能量大小如何?
为了解释这样一个问题,那么这节课我们将从能量的角度来继续研究碰撞问题。
碰撞前 碰撞后 质量 m1 m2 m1 m2
0.25 0.25 0.25 0.25
速度 v1 v2 v1’ v2’
0.44 0.00 0.00 0.44
mv m1v1+m2v2 m1v1’+m2v2’ 0.11 0.11 mv2 0.05 0.05 v/m 1.76 1.76
m1
m2
v1
实验数据分析:碰撞前、后两小车的三个物理量均未发生改变。
一、碰撞中的不变量
新课引入
课堂引入
在两小车碰撞接触面处加装轻弹簧,使两小车碰撞后可以完全弹开。
对比实验一:
回顾
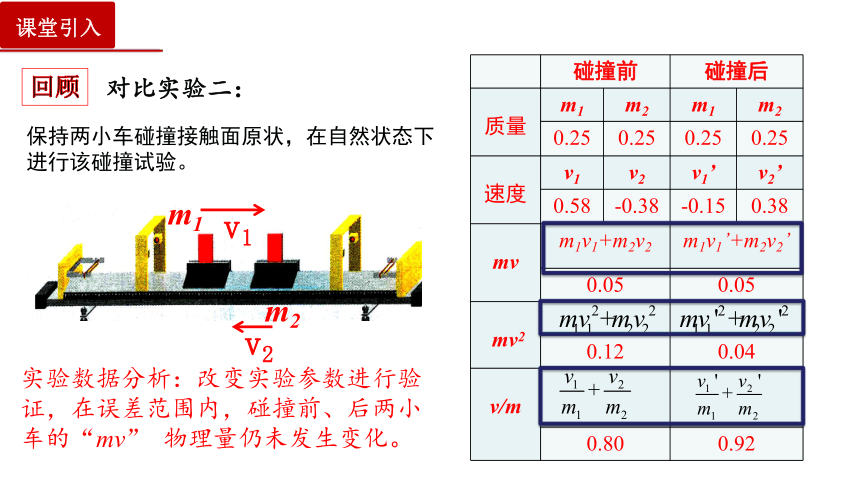
保持两小车碰撞接触面原状,在自然状态下进行该碰撞试验。
实验数据分析:改变实验参数进行验证,在误差范围内,碰撞前、后两小车的“mv” 物理量仍未发生变化。
m1
v1
m2
v2
2
碰撞前 碰撞后 质量 m1 m2 m1 m2
0.25 0.25 0.25 0.25
速度 v1 v2 v1’ v2’
0.58 -0.38 -0.15 0.38
mv m1v1+m2v2 m1v1’+m2v2’ 0.05 0.05 mv2 0.12 0.04 v/m 0.80 0.92
一、课堂引入
新课引入
课堂引入
对比实验二:
回顾
观察碰撞过程两物体的形变的变化, 思考碰撞过程的能量转化情况, 机械能是否守恒
1、弹性碰撞:如果系统在碰撞前后动能不变, 这类碰撞叫作弹性碰撞。
(1). 动量守恒:m1v1 +m2v2 = m1v1'+m2v2'
(2). 动能前后不变: m1v12 + m2v22 = m1v1'2+ m2v2'2
新课讲授
一、弹性碰撞和非弹性碰撞
(机械能守恒)
规律:
例子:如钢球、玻璃球等坚硬球体及间的碰撞皆可视为弹性碰撞,分子、原子间的碰撞也是。
新课讲授
一、弹性碰撞和非弹性碰撞
2、非弹性碰撞:如果系统在碰撞后动能减少, 这类碰撞叫作非弹性碰撞。
(1). 动量守恒:m1v1 + m2v2 = m1v1' + m2v2'
(2). 碰撞后动能减少: m1v12 + m2v22 = m1v1'2 + m2v2'2 + ΔE损失
规律:
碰撞过程两物体不是发生弹性形变时,能量转化情况 机械能是否守恒
机械能不守恒
例子:如橡皮泥球之间的碰撞等。
完全非弹性碰撞,机械能损失最大!!!
v1
静止
m1
m2
v2’
m2
根据动量守恒定律:
弹性碰撞机械能守恒:
碰撞后两个物体的速度:
(简单情形)动碰静: 物体m1以速度v1与原来静止的物体m2发生弹性碰撞,碰撞后它们的速度分别为v1' 和v2' 。用m1、m2、v1表示v1' 和v2' 的公式。
v1’
m1
二、弹性碰撞和非弹性碰撞的实例分析
1、弹性碰撞的实例分析
碰撞后两个物体的速度:
分析:(1)当m1=m2时,v1′=0,v2′=v1(质量相等,速度交换)
(2)当m1 m2时,v1′=-v1,v2′=0(极小碰极大,小等速率反弹,大不变)
(3)当m1 m2时,v1′=v0,v2′=2v1(极大碰极小,大不变,小加倍)
二、弹性碰撞和非弹性碰撞的实例分析
思考:若v2=0时,结论与前面的是否相同?
二、弹性碰撞和非弹性碰撞的实例分析
1、弹性碰撞的实例分析
(复杂情形)动碰动:若在一光滑水平面上有两个质量分别为m1、m2的刚性小球A和B,以初速度v1、v2运动,若它们能发生碰撞(为一维弹性碰撞),碰撞后它们的速度分别为v'1和v'2分别是多大?
根据动量守恒定律:
弹性碰撞机械能守恒:
碰撞后两个物体的速度:
【例题场景】两个物体的质量都是m,碰撞以前一个物体静止,另一个以速度v向它撞去。碰撞以后两个物体粘在一起,成为一个质量为2m的物体,以一定的速度继续前进。碰撞后该系统的总动能是否会有损失?
v
静止
m
m
v’
2m
根据动量守恒定律:
碰撞后的共同速度:
碰撞前的总动能:
碰撞后的总动能:
可见,碰撞后系统的总动能小于碰撞前系统的总动能。
新课讲授
新课讲授
二、弹性碰撞和非弹性碰撞的实例分析
2、非弹性碰撞的实例分析
(1)动量守恒:即p1+p2=p1′+p2′.
(2)动能不增:即Ek1+Ek2 ≥ Ek1′+Ek2′.
(3)速度合理(物理情景要合理):
①若碰前两物体同向运动,则应有v后 > v前,碰后原来在前的物体速度一定增大,若碰后两物体同向运动,则应有v前′ ≥ v后′。
②碰前两物体相向运动,碰后两物体的运动方向不可能都不改变。
新课讲授
新课讲授
二、弹性碰撞和非弹性碰撞的实例分析
3、碰撞三原则
思考与讨论:
通过对非弹性碰撞和弹性碰撞规律的探讨,你是否可以利用你所学到的知识解释一下上课前我们所演示的实验现象,为什么三球叠放时最上面的小球会弹的更高?
新课讲授
新课讲授
三、常见的一些“类碰撞”模型
(1)动量守恒:
(2)能量守恒:
1、子弹打木块模型
(完全非弹性碰撞)
2、板块模型
(1)动量守恒:
(2)能量守恒:
(完全非弹性碰撞)
新课讲授
新课讲授
三、常见的一些“类碰撞”模型
(1)最高点:
(2)分离点:
3、曲面斜面模型(小球不飞出)
水平方向动量守恒:
机械能守恒:
水平方向动量守恒:
机械能守恒:
思考与讨论:
若小球飞出,小球后做何种运动,如何求解?
(弹性碰撞)
(完全非弹性碰撞)
新课讲授
新课讲授
三、常见的一些“类碰撞”模型
4、弹簧模型
(1)从开始到共速:
(2)从开始到第一次恢复原长:
动量守恒:m1v0 = m1v1 + m2v2
动能不变: m1v02 = m1v12 + m2v22
(完全非弹性碰撞)
(弹性碰撞)
临界点分析
①共速:
弹簧形变最大(最短或最长), 势能最大
②恢复原长:弹性势能为0
过程分析
动量守恒:m1v0 = (m1+m2)v
能量守恒: Ep = m1v02 ─ (m1+ m2)v2
弹性碰撞和
非弹性碰撞
弹性碰撞
非弹性碰撞
①动量守恒:
②机械能不守恒:
①动碰静
②动碰动
新课讲授
新课讲授
四、课堂小结
第一章 动量守恒定律
第5节 弹性碰撞与非弹性碰撞
新教材人教版 物理(高中选择性必修第一册)
新课引入
课堂引入
思考与讨论:
2.实验时,为什么将球叠放在一起,最上面的球就能被弹到很高的位置?
1.小球被弹的很高,说明小球具有的能量大小如何?
为了解释这样一个问题,那么这节课我们将从能量的角度来继续研究碰撞问题。
碰撞前 碰撞后 质量 m1 m2 m1 m2
0.25 0.25 0.25 0.25
速度 v1 v2 v1’ v2’
0.44 0.00 0.00 0.44
mv m1v1+m2v2 m1v1’+m2v2’ 0.11 0.11 mv2 0.05 0.05 v/m 1.76 1.76
m1
m2
v1
实验数据分析:碰撞前、后两小车的三个物理量均未发生改变。
一、碰撞中的不变量
新课引入
课堂引入
在两小车碰撞接触面处加装轻弹簧,使两小车碰撞后可以完全弹开。
对比实验一:
回顾
保持两小车碰撞接触面原状,在自然状态下进行该碰撞试验。
实验数据分析:改变实验参数进行验证,在误差范围内,碰撞前、后两小车的“mv” 物理量仍未发生变化。
m1
v1
m2
v2
2
碰撞前 碰撞后 质量 m1 m2 m1 m2
0.25 0.25 0.25 0.25
速度 v1 v2 v1’ v2’
0.58 -0.38 -0.15 0.38
mv m1v1+m2v2 m1v1’+m2v2’ 0.05 0.05 mv2 0.12 0.04 v/m 0.80 0.92
一、课堂引入
新课引入
课堂引入
对比实验二:
回顾
观察碰撞过程两物体的形变的变化, 思考碰撞过程的能量转化情况, 机械能是否守恒
1、弹性碰撞:如果系统在碰撞前后动能不变, 这类碰撞叫作弹性碰撞。
(1). 动量守恒:m1v1 +m2v2 = m1v1'+m2v2'
(2). 动能前后不变: m1v12 + m2v22 = m1v1'2+ m2v2'2
新课讲授
一、弹性碰撞和非弹性碰撞
(机械能守恒)
规律:
例子:如钢球、玻璃球等坚硬球体及间的碰撞皆可视为弹性碰撞,分子、原子间的碰撞也是。
新课讲授
一、弹性碰撞和非弹性碰撞
2、非弹性碰撞:如果系统在碰撞后动能减少, 这类碰撞叫作非弹性碰撞。
(1). 动量守恒:m1v1 + m2v2 = m1v1' + m2v2'
(2). 碰撞后动能减少: m1v12 + m2v22 = m1v1'2 + m2v2'2 + ΔE损失
规律:
碰撞过程两物体不是发生弹性形变时,能量转化情况 机械能是否守恒
机械能不守恒
例子:如橡皮泥球之间的碰撞等。
完全非弹性碰撞,机械能损失最大!!!
v1
静止
m1
m2
v2’
m2
根据动量守恒定律:
弹性碰撞机械能守恒:
碰撞后两个物体的速度:
(简单情形)动碰静: 物体m1以速度v1与原来静止的物体m2发生弹性碰撞,碰撞后它们的速度分别为v1' 和v2' 。用m1、m2、v1表示v1' 和v2' 的公式。
v1’
m1
二、弹性碰撞和非弹性碰撞的实例分析
1、弹性碰撞的实例分析
碰撞后两个物体的速度:
分析:(1)当m1=m2时,v1′=0,v2′=v1(质量相等,速度交换)
(2)当m1 m2时,v1′=-v1,v2′=0(极小碰极大,小等速率反弹,大不变)
(3)当m1 m2时,v1′=v0,v2′=2v1(极大碰极小,大不变,小加倍)
二、弹性碰撞和非弹性碰撞的实例分析
思考:若v2=0时,结论与前面的是否相同?
二、弹性碰撞和非弹性碰撞的实例分析
1、弹性碰撞的实例分析
(复杂情形)动碰动:若在一光滑水平面上有两个质量分别为m1、m2的刚性小球A和B,以初速度v1、v2运动,若它们能发生碰撞(为一维弹性碰撞),碰撞后它们的速度分别为v'1和v'2分别是多大?
根据动量守恒定律:
弹性碰撞机械能守恒:
碰撞后两个物体的速度:
【例题场景】两个物体的质量都是m,碰撞以前一个物体静止,另一个以速度v向它撞去。碰撞以后两个物体粘在一起,成为一个质量为2m的物体,以一定的速度继续前进。碰撞后该系统的总动能是否会有损失?
v
静止
m
m
v’
2m
根据动量守恒定律:
碰撞后的共同速度:
碰撞前的总动能:
碰撞后的总动能:
可见,碰撞后系统的总动能小于碰撞前系统的总动能。
新课讲授
新课讲授
二、弹性碰撞和非弹性碰撞的实例分析
2、非弹性碰撞的实例分析
(1)动量守恒:即p1+p2=p1′+p2′.
(2)动能不增:即Ek1+Ek2 ≥ Ek1′+Ek2′.
(3)速度合理(物理情景要合理):
①若碰前两物体同向运动,则应有v后 > v前,碰后原来在前的物体速度一定增大,若碰后两物体同向运动,则应有v前′ ≥ v后′。
②碰前两物体相向运动,碰后两物体的运动方向不可能都不改变。
新课讲授
新课讲授
二、弹性碰撞和非弹性碰撞的实例分析
3、碰撞三原则
思考与讨论:
通过对非弹性碰撞和弹性碰撞规律的探讨,你是否可以利用你所学到的知识解释一下上课前我们所演示的实验现象,为什么三球叠放时最上面的小球会弹的更高?
新课讲授
新课讲授
三、常见的一些“类碰撞”模型
(1)动量守恒:
(2)能量守恒:
1、子弹打木块模型
(完全非弹性碰撞)
2、板块模型
(1)动量守恒:
(2)能量守恒:
(完全非弹性碰撞)
新课讲授
新课讲授
三、常见的一些“类碰撞”模型
(1)最高点:
(2)分离点:
3、曲面斜面模型(小球不飞出)
水平方向动量守恒:
机械能守恒:
水平方向动量守恒:
机械能守恒:
思考与讨论:
若小球飞出,小球后做何种运动,如何求解?
(弹性碰撞)
(完全非弹性碰撞)
新课讲授
新课讲授
三、常见的一些“类碰撞”模型
4、弹簧模型
(1)从开始到共速:
(2)从开始到第一次恢复原长:
动量守恒:m1v0 = m1v1 + m2v2
动能不变: m1v02 = m1v12 + m2v22
(完全非弹性碰撞)
(弹性碰撞)
临界点分析
①共速:
弹簧形变最大(最短或最长), 势能最大
②恢复原长:弹性势能为0
过程分析
动量守恒:m1v0 = (m1+m2)v
能量守恒: Ep = m1v02 ─ (m1+ m2)v2
弹性碰撞和
非弹性碰撞
弹性碰撞
非弹性碰撞
①动量守恒:
②机械能不守恒:
①动碰静
②动碰动
新课讲授
新课讲授
四、课堂小结
