2023—2024学年冀教版数学七年级上册第五章 一元一次方程 复习课课件(36张ppt)
文档属性
| 名称 | 2023—2024学年冀教版数学七年级上册第五章 一元一次方程 复习课课件(36张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-27 18:33:48 | ||
图片预览











文档简介
(共36张PPT)
第五章 一元一次方程
第五章 复习课
1.知道一元一次方程及它的解的概念,会检验一个数是不是某个方程的解.
2.知道等式的基本性质,会解一元一次方程.
3.能找出实际问题中的未知量与已知量,并能利用它们之间的关系列出一元一次方程解决实际问题.
◎重点:等式的性质、一元一次方程的解法及应用.
◎难点:一元一次方程的应用.
这一章我们重点学习了一元一次方程的有关概念、解法和应用,你能将本章的知识梳理成一个知识结构图吗?能回忆起所学的重点知识吗?
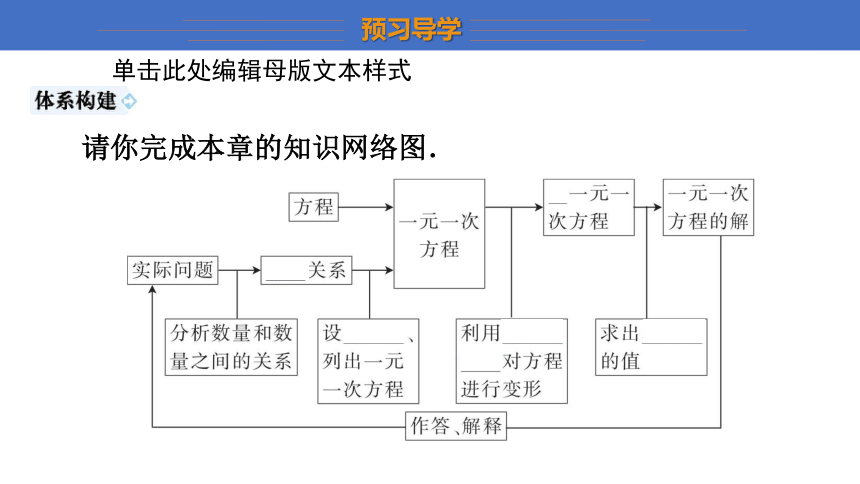
请你完成本章的知识网络图.
1.含有未知数的 等式 叫做方程,能使方程两边 相等 的未知数的值,叫做方程的解.
2.如果方程中含有 一 个未知数(也称元),并且所含未知数的项的次数是 1 ,那么我们把这样的方程叫做一元一次方程.
等式
相等
一
1
3.等式的基本性质:(1)等式的两边加上(或 减去 )同一个数或同一个 整式 ,结果仍是等式,即如果a=b,那么a ± c=b ± c.(2)等式的两边乘(或 除以 )同一个数(除数不等于0),结果仍是等式,即如果a=b,那么ac= bc (或=,c ≠ 0).
减去
整式
±
±
除以
bc
≠
4.在解方程的过程中,等号的两边加上(或减去)方程中某一项的变形过程,相当于将这一项 改变符号 后,从等号的一边 移到 另一边,这种变形过程叫做移项.
5.解一元一次方程的步骤,一般是:(1) 去分母 ;(2) 去括号 ;(3) 移项 ;(4) 合并同类项 (化为ax=b)的形式,其中a、b是已知数);(5)将未知数的系数 化为1 (化为x=c的形式).
改变符号
移到
去分母
去括号
移项
合并同类项
化为1
6.列一元一次方程组解应用题的一般步骤:(1)审:弄清题意和题目中的 数量关系 .(2)设:用字母表示题中的 未知数 ;(3)找:分析题意,找出题中的 等量关系 ;(4)列:根据 等量关系 列出方程;(5)解:解这个方程,求出未知数的值;(6)答:检验并写出答案(包括单位名称).
数量关系
未知数
等量关系
等量关系
预习导学部分可以以教师提问学生回答的形式完成,建议学生在课前对不熟悉的知识进行复习,预习导学部分建议教师用10分钟左右的时间完成.
·导学建议·
一元一次方程的有关概念
1.下列方程:=,=,③2(x+1)+3=,④3(2x+5)-2(x-1)=3x+6.其中一元一次方程有( B )
A.1个 B.2个 C.3个 D.4个
B
【方法归纳交流】一元一次方程必须满足三个条件:①只含有 一 个未知数;②未知数的最高次数为 1 ;③是 整式 方程.
【变式拓展】若关于x的方程2xm+2m=0是一元一次方程,则m的值是( B )
A. B.1 C.3 D.不存在
一
1
整
式
B
1.若(m-1)x|m|=m+2n是关于x的一元一次方程,且n是它的解,则n-m= .
2.若关于x的一元一次方程-=1的解是x=-1,则k的值是( B )
A. B.1 C.- D.0
【方法归纳交流】方程的解能使方程左右两边的值 相等 ;反过来,能使方程左右两边的值 相等 的未知数的值是方程的解.
B
相
等
相等
·导学建议·
一元一次方程的定义和解的定义是各类考试考查的重点,一元一次方程的定义重点考查未知数的最高次数为1和系数不等于0,一元一次方程解的定义重点考查已知方程的解求方程中字母的取值,因此教学时要加强这两类题目的练习.
等式的基本性质
2.如图,在甲图中的左盘上将两个物品取下一个,为了使天平仍然平衡,需要从乙图中右盘取下( A )
A.3个 B.4个 C.5个 D.6个
A
3.已知等式2x-y+3=0,则下列每一步变形是否一定成立?若一定成立,说明变形依据;若不成立,请说明理由.
(1)由2x-y+3=0,得2x-y=-3;
(2)由2x-y+3=0,得2x=y-3;
(3)由2x-y+3=0,得x=(y-3);
(4)由2x-y+3=0,得y=2x-3.
解:(1)成立,根据等式的基本性质1,等号两边同时减去3.
(2)成立,根据等式的基本性质1,等号两边同时加上y-3.
(3)成立,在(2)的基础上,由等式的基本性质2,等号两边同时除以2.
(4)不成立,根据等式的基本性质1,等号两边都加上y,得y=2x+3.
【方法归纳交流】等式的性质必须是等号两边用 相同 的数做 相同 的运算.
相同
相同
一元一次方程的解法
4.根据右边流程图中的程序,当输出的数值y为1时,输入数值x为( C )
A.-8
B.8
C.-8或8
D.不存在
5.如果与互为相反数,则x= .
C
6.解方程:-1=-.
解:去分母,得10(3x+2)-20=5(2x-1)-4(2x+1),
去括号,得30x+20-20=10x-5-8x-4,
移项,得30x-10x+8x=-5-4-20+20,
合并同类项,得28x=-9,
系数化为1,得x=-.
【变式演练】当x的值等于多少时,代数式的值比-的值大1?
解:由题意得-1=-,
解得x=-,
所以当x=-时,代数式的值比-的值大1.
【方法归纳交流】在解方程时,应该注意以下几点:(1)去分母时,各项都要乘以 最简公分母 ,包括不含 分母 的项;(2)去括号时,括号外的因数要和括号内的 每一项 都相乘,并且注意 符号 ;(3)移项要 变号 ;(4)系数化为1时要分清楚除数和 被除数 .
最简公分母
分母
每一项
符号
变号
被除数
解方程-=1.
解:原方程可化为-=1,
去分母,得3(4y+9)-5(3+2y)=15,
去括号,得12y+27-15-10y=15,
移项、合并,得2y=3,
系数化为1,得y=.
·导学建议·
一元一次方程的解法是必须掌握的内容,教学时可以通过展示不同的题目,让学生在学会一元一次方程解法的同时,体会一元一次方程解法的应用.备选题中分数的分子、分母化为整数是学生易错的地方,注意和去分母进行比较两者的异同.
列一元一次方程解应用
7.一件工程,甲单独做40天完成,乙单独做30天完成,丙单独做24天完成.甲、乙、丙合作3天后,乙、丙有事离开若干天,乙离开的天数比丙多3天,结果前后共用14天完成全部工作,问途中乙、丙各离开多少天?
解得x=4(天),
x+3=7(天).
答:途中乙离开7天,丙离开4天.
解:设丙离开x天,则乙离开(x+3)天.
由题意可得++=1,
8.一队学生从学校出发去部队军训,行走速度是5 km/h,走了30 min时,一通讯员按原来的路线返回学校报信,然后他追赶队伍,通讯员的速度是14 km/h.他在距部队10 km处追上队伍,求学校到部队的距离.
解:设该通讯员从返回到追上队伍用的时间是x h.
由题意,得5×+5x=14x-5×,解得x= (h).
则学校到部队的距离为5×+5×+10=(km).
答:学校到部队的距离为 km.
9.有甲、乙两个圆柱体容器,底面半径之比为3∶2,甲容器水深20 cm,乙容器水深10 cm,再往两个容器注入同样多的水,使两个容器的水深相等,这时水深多少cm?
由甲、乙两个圆柱体容器,底面半径之比为3∶2,若设甲的半径为3a,则乙的半径为 2a .
解:设甲的半径为3a,乙的半径为2a,水深为x cm.
依题意得π×9a2·(x-20)=π×4a2×(x-10),
解得x=28(cm).
答:这时水深28 cm.
2a
10.有一个商店把某件商品按进价加20%作为定价,可是总是卖不出去,后来老板按定价减价20%以96元出售,很快就卖掉了.求这件商品的进价.
解:设这种商品的进价为x元.
根据题意得(1-20%)(1+20%)x=96,
解得x=100(元).
答:这件商品的进价为100元.
·导学建议·
便于学生寻找题目中的等量关系,可以先让其填写下列表格:
进价 定价 减价20%后的价格 售价
x (1+20%)x (1-20%)(1+20%)x 96
【变式拓展】在上述买卖中,该商店是亏了还是赚了?亏或赚了多少钱?
解:96-100=-4(元).
答:在上述买卖中该商店亏了4元.
11.如图,将一副三角尺的直角顶点重合在一起,若∠DOB与∠DOA的比是2∶11,求∠BOC的度数.
解:设∠DOB=2x,则∠DOA=11x.
因为∠AOB=∠COD,所以∠AOC=∠DOB=2x,∠BOC=7x.
又因为∠AOD=∠AOB+∠COD-∠BOC=180°-∠BOC,则可得方程11x=180-7x,
解得x=10°,所以∠BOC=70°.
【方法归纳交流】列方程解应用题的关键,是从题目中找到 等量关系 列方程.
·导学建议·
等量关系
一元一次方程的应用是本章的重点,在列方程时,主要本着“各分量之和等于总量”“同一个量的不同表示”“几何量之间的关系”等列方程,提醒学生注意解决这类问题的关键是从题目中寻找等量关系.
第五章 一元一次方程
第五章 复习课
1.知道一元一次方程及它的解的概念,会检验一个数是不是某个方程的解.
2.知道等式的基本性质,会解一元一次方程.
3.能找出实际问题中的未知量与已知量,并能利用它们之间的关系列出一元一次方程解决实际问题.
◎重点:等式的性质、一元一次方程的解法及应用.
◎难点:一元一次方程的应用.
这一章我们重点学习了一元一次方程的有关概念、解法和应用,你能将本章的知识梳理成一个知识结构图吗?能回忆起所学的重点知识吗?
请你完成本章的知识网络图.
1.含有未知数的 等式 叫做方程,能使方程两边 相等 的未知数的值,叫做方程的解.
2.如果方程中含有 一 个未知数(也称元),并且所含未知数的项的次数是 1 ,那么我们把这样的方程叫做一元一次方程.
等式
相等
一
1
3.等式的基本性质:(1)等式的两边加上(或 减去 )同一个数或同一个 整式 ,结果仍是等式,即如果a=b,那么a ± c=b ± c.(2)等式的两边乘(或 除以 )同一个数(除数不等于0),结果仍是等式,即如果a=b,那么ac= bc (或=,c ≠ 0).
减去
整式
±
±
除以
bc
≠
4.在解方程的过程中,等号的两边加上(或减去)方程中某一项的变形过程,相当于将这一项 改变符号 后,从等号的一边 移到 另一边,这种变形过程叫做移项.
5.解一元一次方程的步骤,一般是:(1) 去分母 ;(2) 去括号 ;(3) 移项 ;(4) 合并同类项 (化为ax=b)的形式,其中a、b是已知数);(5)将未知数的系数 化为1 (化为x=c的形式).
改变符号
移到
去分母
去括号
移项
合并同类项
化为1
6.列一元一次方程组解应用题的一般步骤:(1)审:弄清题意和题目中的 数量关系 .(2)设:用字母表示题中的 未知数 ;(3)找:分析题意,找出题中的 等量关系 ;(4)列:根据 等量关系 列出方程;(5)解:解这个方程,求出未知数的值;(6)答:检验并写出答案(包括单位名称).
数量关系
未知数
等量关系
等量关系
预习导学部分可以以教师提问学生回答的形式完成,建议学生在课前对不熟悉的知识进行复习,预习导学部分建议教师用10分钟左右的时间完成.
·导学建议·
一元一次方程的有关概念
1.下列方程:=,=,③2(x+1)+3=,④3(2x+5)-2(x-1)=3x+6.其中一元一次方程有( B )
A.1个 B.2个 C.3个 D.4个
B
【方法归纳交流】一元一次方程必须满足三个条件:①只含有 一 个未知数;②未知数的最高次数为 1 ;③是 整式 方程.
【变式拓展】若关于x的方程2xm+2m=0是一元一次方程,则m的值是( B )
A. B.1 C.3 D.不存在
一
1
整
式
B
1.若(m-1)x|m|=m+2n是关于x的一元一次方程,且n是它的解,则n-m= .
2.若关于x的一元一次方程-=1的解是x=-1,则k的值是( B )
A. B.1 C.- D.0
【方法归纳交流】方程的解能使方程左右两边的值 相等 ;反过来,能使方程左右两边的值 相等 的未知数的值是方程的解.
B
相
等
相等
·导学建议·
一元一次方程的定义和解的定义是各类考试考查的重点,一元一次方程的定义重点考查未知数的最高次数为1和系数不等于0,一元一次方程解的定义重点考查已知方程的解求方程中字母的取值,因此教学时要加强这两类题目的练习.
等式的基本性质
2.如图,在甲图中的左盘上将两个物品取下一个,为了使天平仍然平衡,需要从乙图中右盘取下( A )
A.3个 B.4个 C.5个 D.6个
A
3.已知等式2x-y+3=0,则下列每一步变形是否一定成立?若一定成立,说明变形依据;若不成立,请说明理由.
(1)由2x-y+3=0,得2x-y=-3;
(2)由2x-y+3=0,得2x=y-3;
(3)由2x-y+3=0,得x=(y-3);
(4)由2x-y+3=0,得y=2x-3.
解:(1)成立,根据等式的基本性质1,等号两边同时减去3.
(2)成立,根据等式的基本性质1,等号两边同时加上y-3.
(3)成立,在(2)的基础上,由等式的基本性质2,等号两边同时除以2.
(4)不成立,根据等式的基本性质1,等号两边都加上y,得y=2x+3.
【方法归纳交流】等式的性质必须是等号两边用 相同 的数做 相同 的运算.
相同
相同
一元一次方程的解法
4.根据右边流程图中的程序,当输出的数值y为1时,输入数值x为( C )
A.-8
B.8
C.-8或8
D.不存在
5.如果与互为相反数,则x= .
C
6.解方程:-1=-.
解:去分母,得10(3x+2)-20=5(2x-1)-4(2x+1),
去括号,得30x+20-20=10x-5-8x-4,
移项,得30x-10x+8x=-5-4-20+20,
合并同类项,得28x=-9,
系数化为1,得x=-.
【变式演练】当x的值等于多少时,代数式的值比-的值大1?
解:由题意得-1=-,
解得x=-,
所以当x=-时,代数式的值比-的值大1.
【方法归纳交流】在解方程时,应该注意以下几点:(1)去分母时,各项都要乘以 最简公分母 ,包括不含 分母 的项;(2)去括号时,括号外的因数要和括号内的 每一项 都相乘,并且注意 符号 ;(3)移项要 变号 ;(4)系数化为1时要分清楚除数和 被除数 .
最简公分母
分母
每一项
符号
变号
被除数
解方程-=1.
解:原方程可化为-=1,
去分母,得3(4y+9)-5(3+2y)=15,
去括号,得12y+27-15-10y=15,
移项、合并,得2y=3,
系数化为1,得y=.
·导学建议·
一元一次方程的解法是必须掌握的内容,教学时可以通过展示不同的题目,让学生在学会一元一次方程解法的同时,体会一元一次方程解法的应用.备选题中分数的分子、分母化为整数是学生易错的地方,注意和去分母进行比较两者的异同.
列一元一次方程解应用
7.一件工程,甲单独做40天完成,乙单独做30天完成,丙单独做24天完成.甲、乙、丙合作3天后,乙、丙有事离开若干天,乙离开的天数比丙多3天,结果前后共用14天完成全部工作,问途中乙、丙各离开多少天?
解得x=4(天),
x+3=7(天).
答:途中乙离开7天,丙离开4天.
解:设丙离开x天,则乙离开(x+3)天.
由题意可得++=1,
8.一队学生从学校出发去部队军训,行走速度是5 km/h,走了30 min时,一通讯员按原来的路线返回学校报信,然后他追赶队伍,通讯员的速度是14 km/h.他在距部队10 km处追上队伍,求学校到部队的距离.
解:设该通讯员从返回到追上队伍用的时间是x h.
由题意,得5×+5x=14x-5×,解得x= (h).
则学校到部队的距离为5×+5×+10=(km).
答:学校到部队的距离为 km.
9.有甲、乙两个圆柱体容器,底面半径之比为3∶2,甲容器水深20 cm,乙容器水深10 cm,再往两个容器注入同样多的水,使两个容器的水深相等,这时水深多少cm?
由甲、乙两个圆柱体容器,底面半径之比为3∶2,若设甲的半径为3a,则乙的半径为 2a .
解:设甲的半径为3a,乙的半径为2a,水深为x cm.
依题意得π×9a2·(x-20)=π×4a2×(x-10),
解得x=28(cm).
答:这时水深28 cm.
2a
10.有一个商店把某件商品按进价加20%作为定价,可是总是卖不出去,后来老板按定价减价20%以96元出售,很快就卖掉了.求这件商品的进价.
解:设这种商品的进价为x元.
根据题意得(1-20%)(1+20%)x=96,
解得x=100(元).
答:这件商品的进价为100元.
·导学建议·
便于学生寻找题目中的等量关系,可以先让其填写下列表格:
进价 定价 减价20%后的价格 售价
x (1+20%)x (1-20%)(1+20%)x 96
【变式拓展】在上述买卖中,该商店是亏了还是赚了?亏或赚了多少钱?
解:96-100=-4(元).
答:在上述买卖中该商店亏了4元.
11.如图,将一副三角尺的直角顶点重合在一起,若∠DOB与∠DOA的比是2∶11,求∠BOC的度数.
解:设∠DOB=2x,则∠DOA=11x.
因为∠AOB=∠COD,所以∠AOC=∠DOB=2x,∠BOC=7x.
又因为∠AOD=∠AOB+∠COD-∠BOC=180°-∠BOC,则可得方程11x=180-7x,
解得x=10°,所以∠BOC=70°.
【方法归纳交流】列方程解应用题的关键,是从题目中找到 等量关系 列方程.
·导学建议·
等量关系
一元一次方程的应用是本章的重点,在列方程时,主要本着“各分量之和等于总量”“同一个量的不同表示”“几何量之间的关系”等列方程,提醒学生注意解决这类问题的关键是从题目中寻找等量关系.
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
