2023—2024学年苏科版数学八年级上册 期末检测试题(无答案)
文档属性
| 名称 | 2023—2024学年苏科版数学八年级上册 期末检测试题(无答案) | 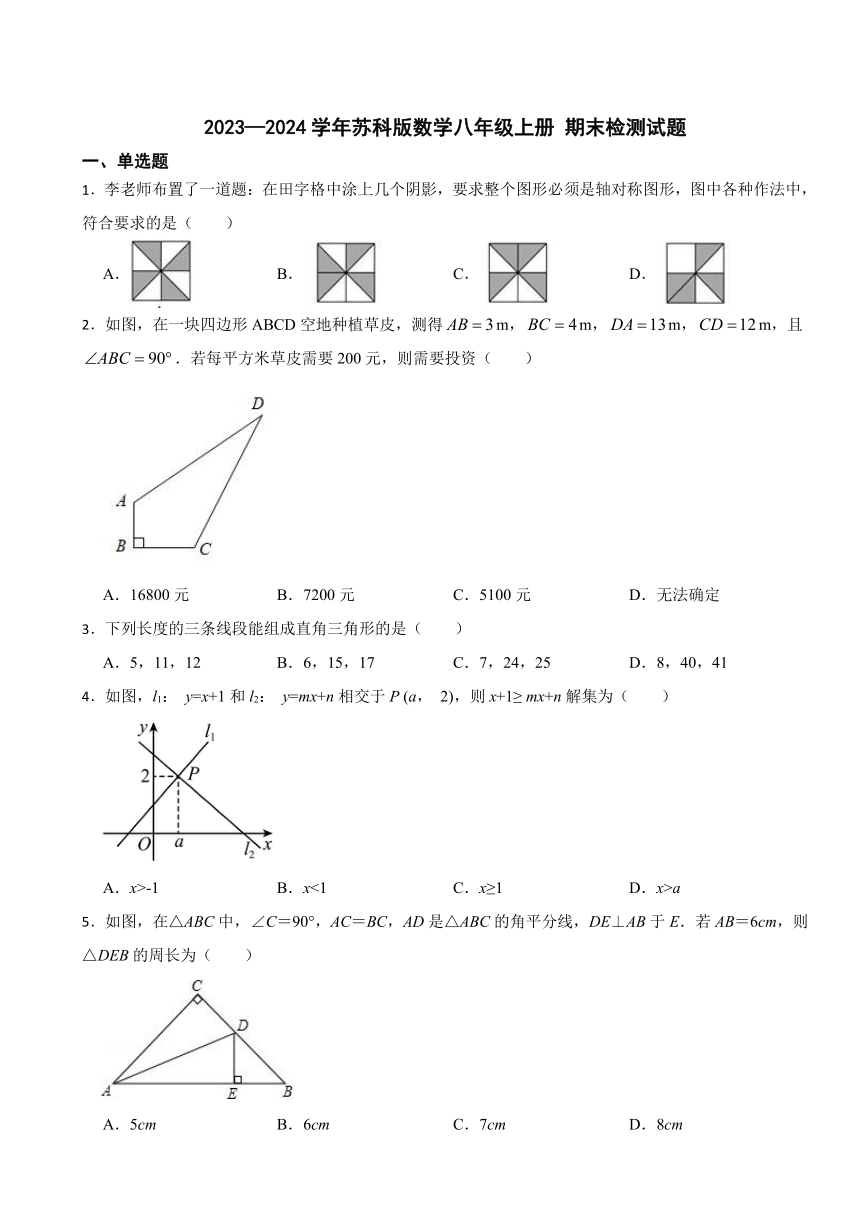 | |
| 格式 | docx | ||
| 文件大小 | 313.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-27 20:03:39 | ||
图片预览

文档简介
2023—2024学年苏科版数学八年级上册 期末检测试题
一、单选题
1.李老师布置了一道题:在田字格中涂上几个阴影,要求整个图形必须是轴对称图形,图中各种作法中,符合要求的是( )
A. B. C. D.
2.如图,在一块四边形ABCD空地种植草皮,测得m,m,m,m,且.若每平方米草皮需要200元,则需要投资( )
A.16800元 B.7200元 C.5100元 D.无法确定
3.下列长度的三条线段能组成直角三角形的是( )
A.5,11,12 B.6,15,17 C.7,24,25 D.8,40,41
4.如图,l1: y=x+1和l2: y=mx+n相交于P (a, 2),则x+1≥ mx+n解集为( )
A.x>-1 B.x<1 C.x≥1 D.x>a
5.如图,在△ABC中,∠C=90°,AC=BC,AD是△ABC的角平分线,DE⊥AB于E.若AB=6cm,则△DEB的周长为( )
A.5cm B.6cm C.7cm D.8cm
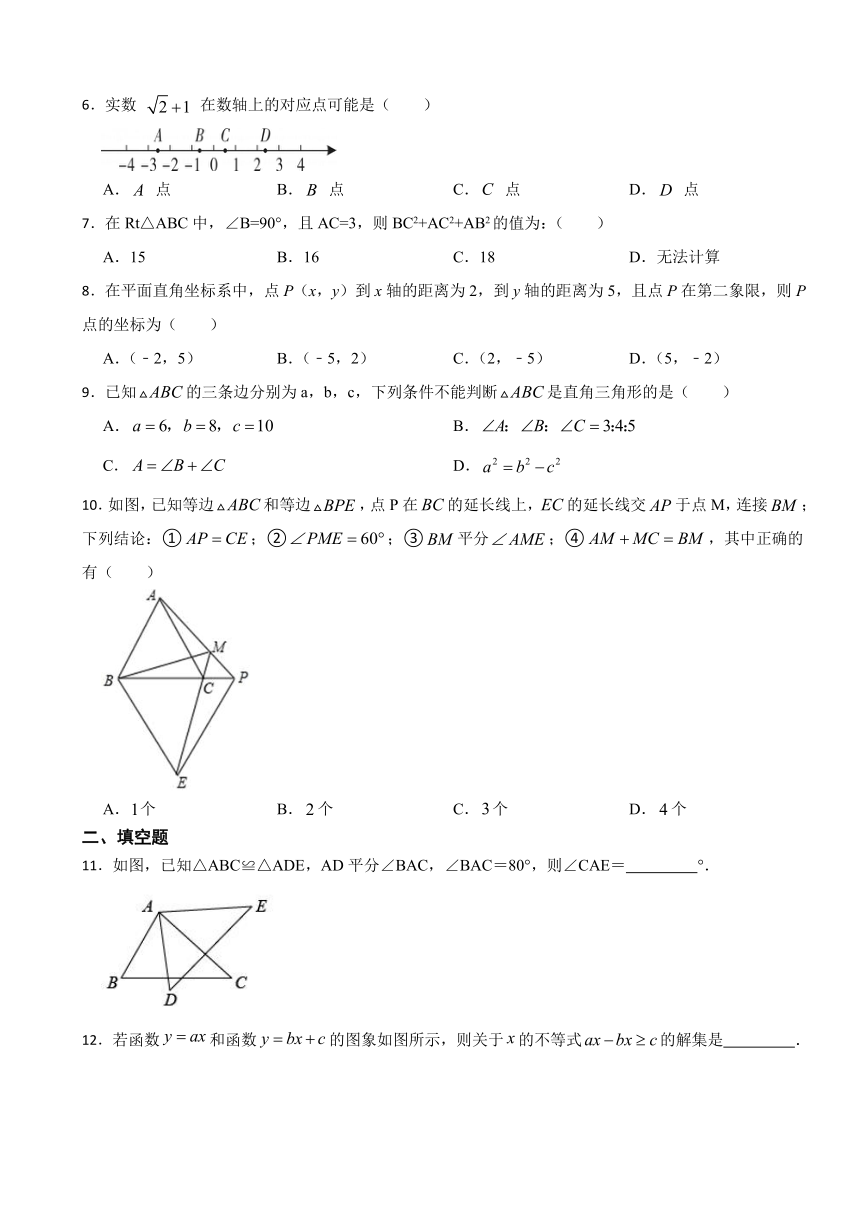
6.实数 在数轴上的对应点可能是( )
A. 点 B. 点 C. 点 D. 点
7.在Rt△ABC中,∠B=90°,且AC=3,则BC2+AC2+AB2的值为:( )
A.15 B.16 C.18 D.无法计算
8.在平面直角坐标系中,点P(x,y)到x轴的距离为2,到y轴的距离为5,且点P在第二象限,则P点的坐标为( )
A.(﹣2,5) B.(﹣5,2) C.(2,﹣5) D.(5,﹣2)
9.已知的三条边分别为a,b,c,下列条件不能判断是直角三角形的是( )
A. B.
C. D.
10.如图,已知等边和等边,点P在的延长线上,的延长线交于点M,连接;下列结论:①;②;③平分;④,其中正确的有( )
A.个 B.个 C.个 D.个
二、填空题
11.如图,已知△ABC≌△ADE,AD平分∠BAC,∠BAC=80°,则∠CAE= °.
12.若函数和函数的图象如图所示,则关于的不等式的解集是 .
13.若△ABC的三边长分别为a,b,c.下列条件:①∠A=∠B﹣∠C;②a2=(b+c)(b﹣c);③∠A:∠B:∠C=3:4:5;④a:b:c=5:12:13.其中能判断△ABC是直角三角形的是 (填序号).
14.已知:如图, 为 的角平分线,且 ,E为 延长线上的一点, ,过E作 ,F为垂足,下列结论:① ;② ;③ ;④ ,其中正确的是 .(填序号)
15.如图, 为⊙O的直径, 是⊙O上的两点,过A作 于点C,过B作 于点D,P为 上的任意一点,若 , , ,则 的最小值是 .
三、计算题
16.利用平方根求下列x的值:
(1)x2=16
(2)3(x+2)2=27
四、解答题
17.如图,点B、C、E、F在一条直线上,AB=DC,AE=DF,BF=CE.求证:∠A=∠D.
18.如图,已知在Rt△ABC中,∠ACB=90°,AC=9,BC=12,AB的垂直平分线交AB于点D,交BC于点E,连结AE,求BE的长.
19.为绿化校园,某校计划购进A、B两种树苗,共21课.已知A种树苗每棵90元,B种树苗每棵70元.设购买B种树苗x棵,购买两种树苗所需费用为y元.
(1)y与x的函数关系式;
(2)若购买B种树苗的数量少于A种树苗的数量,请给出一种费用最省的方案,并求出该方案所需费用.
20.如图, 于点 于点 , 求证: .
21.如图,一高层住宅发生火灾,消防车立即赶到距大厦8米处(车尼AE到大厦墙面CD),升起云梯到火灾窗口B,已知云梯AB长17米,云梯底部距地面的高AE=1.5米;问发生火灾的住户窗口距离地面多高?
22.如图,在△ABC中,AB=AC,E是AB上一点,且DE=AE.
(1)求证:DE∥AC;
(2)若∠EDA=24°,求∠C的度数.
23.如图,在△ABC中,∠ACB=90°,AC=BC,若过点C在△ABC内作直线MN,AM⊥MN于点M,BN⊥MN于点N,则AM、BN与MN之间有什么关系?请说明理由.
24.如图①,在数轴上,点为坐标原点,点、、、表示的数分别是-8、3、9、13.动点、同时出发,动点从点出发,沿数轴以每秒2个单位的速度向点运动,当点运动到点后,立即按原来的速度返回.动点从点出发,沿数轴以每秒1个単位的速度向终点运动.当点到达点时,点也停止运动,设点的运动时间为秒.
(1)点与原点的距离是 .
(2)点从点向点运动过程中,点与原点的距离是 (用含的代数式表示).
(3)点从点向点运动过程中,当点与原点的距离恰好等于点与点的距离时,求的值.
(4)在点、的整个运动过程中,若将数轴在点和点处各折一下,使点与点重合,如图②所示,当所构成的三角形中恰好有两条边相等时,直接写出的值.
一、单选题
1.李老师布置了一道题:在田字格中涂上几个阴影,要求整个图形必须是轴对称图形,图中各种作法中,符合要求的是( )
A. B. C. D.
2.如图,在一块四边形ABCD空地种植草皮,测得m,m,m,m,且.若每平方米草皮需要200元,则需要投资( )
A.16800元 B.7200元 C.5100元 D.无法确定
3.下列长度的三条线段能组成直角三角形的是( )
A.5,11,12 B.6,15,17 C.7,24,25 D.8,40,41
4.如图,l1: y=x+1和l2: y=mx+n相交于P (a, 2),则x+1≥ mx+n解集为( )
A.x>-1 B.x<1 C.x≥1 D.x>a
5.如图,在△ABC中,∠C=90°,AC=BC,AD是△ABC的角平分线,DE⊥AB于E.若AB=6cm,则△DEB的周长为( )
A.5cm B.6cm C.7cm D.8cm
6.实数 在数轴上的对应点可能是( )
A. 点 B. 点 C. 点 D. 点
7.在Rt△ABC中,∠B=90°,且AC=3,则BC2+AC2+AB2的值为:( )
A.15 B.16 C.18 D.无法计算
8.在平面直角坐标系中,点P(x,y)到x轴的距离为2,到y轴的距离为5,且点P在第二象限,则P点的坐标为( )
A.(﹣2,5) B.(﹣5,2) C.(2,﹣5) D.(5,﹣2)
9.已知的三条边分别为a,b,c,下列条件不能判断是直角三角形的是( )
A. B.
C. D.
10.如图,已知等边和等边,点P在的延长线上,的延长线交于点M,连接;下列结论:①;②;③平分;④,其中正确的有( )
A.个 B.个 C.个 D.个
二、填空题
11.如图,已知△ABC≌△ADE,AD平分∠BAC,∠BAC=80°,则∠CAE= °.
12.若函数和函数的图象如图所示,则关于的不等式的解集是 .
13.若△ABC的三边长分别为a,b,c.下列条件:①∠A=∠B﹣∠C;②a2=(b+c)(b﹣c);③∠A:∠B:∠C=3:4:5;④a:b:c=5:12:13.其中能判断△ABC是直角三角形的是 (填序号).
14.已知:如图, 为 的角平分线,且 ,E为 延长线上的一点, ,过E作 ,F为垂足,下列结论:① ;② ;③ ;④ ,其中正确的是 .(填序号)
15.如图, 为⊙O的直径, 是⊙O上的两点,过A作 于点C,过B作 于点D,P为 上的任意一点,若 , , ,则 的最小值是 .
三、计算题
16.利用平方根求下列x的值:
(1)x2=16
(2)3(x+2)2=27
四、解答题
17.如图,点B、C、E、F在一条直线上,AB=DC,AE=DF,BF=CE.求证:∠A=∠D.
18.如图,已知在Rt△ABC中,∠ACB=90°,AC=9,BC=12,AB的垂直平分线交AB于点D,交BC于点E,连结AE,求BE的长.
19.为绿化校园,某校计划购进A、B两种树苗,共21课.已知A种树苗每棵90元,B种树苗每棵70元.设购买B种树苗x棵,购买两种树苗所需费用为y元.
(1)y与x的函数关系式;
(2)若购买B种树苗的数量少于A种树苗的数量,请给出一种费用最省的方案,并求出该方案所需费用.
20.如图, 于点 于点 , 求证: .
21.如图,一高层住宅发生火灾,消防车立即赶到距大厦8米处(车尼AE到大厦墙面CD),升起云梯到火灾窗口B,已知云梯AB长17米,云梯底部距地面的高AE=1.5米;问发生火灾的住户窗口距离地面多高?
22.如图,在△ABC中,AB=AC,E是AB上一点,且DE=AE.
(1)求证:DE∥AC;
(2)若∠EDA=24°,求∠C的度数.
23.如图,在△ABC中,∠ACB=90°,AC=BC,若过点C在△ABC内作直线MN,AM⊥MN于点M,BN⊥MN于点N,则AM、BN与MN之间有什么关系?请说明理由.
24.如图①,在数轴上,点为坐标原点,点、、、表示的数分别是-8、3、9、13.动点、同时出发,动点从点出发,沿数轴以每秒2个单位的速度向点运动,当点运动到点后,立即按原来的速度返回.动点从点出发,沿数轴以每秒1个単位的速度向终点运动.当点到达点时,点也停止运动,设点的运动时间为秒.
(1)点与原点的距离是 .
(2)点从点向点运动过程中,点与原点的距离是 (用含的代数式表示).
(3)点从点向点运动过程中,当点与原点的距离恰好等于点与点的距离时,求的值.
(4)在点、的整个运动过程中,若将数轴在点和点处各折一下,使点与点重合,如图②所示,当所构成的三角形中恰好有两条边相等时,直接写出的值.
同课章节目录
