2023—2024学年苏科版数学九年级上册 期末检测试题(无答案)
文档属性
| 名称 | 2023—2024学年苏科版数学九年级上册 期末检测试题(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 83.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-27 20:46:24 | ||
图片预览

文档简介
2023—2024学年苏科版数学九年级上册 期末检测试题
一、单选题
1.某班10名学生的校服尺寸与对应人数如表所示:
尺寸(cm) 160 165 170 175 180
学生人数(人) 1 3 2 2 2
则这10名学生校服尺寸的众数和中位数分别为( )
A.165cm,165cm B.165cm,170cm C.170cm,165cm D.170cm,170cm
2.某兴趣小组为了解我市气温变化情况,记录了今年月份连续6天的最低气温(单位:℃): ,关于这组数据,下列结论不正确的是( )
A.平均数是 B.中位数是
C.众数是 D.方差是
3.一元二次方程x2-5x+6=0的 解为( )
A.X1=2,x2= -3 B.x1= -2, x2=-3
C.x1=-2,x2=-3 D.x1=2,x2=3
4.淘淘和丽丽是九年级学生,在5月份进行的物理、化学、生物实验技能考试中,考试科目要求三选一,并且采取抽签方式取得,那么他们两人都抽到物理实验的概率是( )
A. B. C. D.
5.已知关于x的方程(2x-m)(mx+1)=(3x+1)(mx-1)有一个根是0,则它的另一个根和m的值分别是( )
A.3和1 B.2和3 C.3和4 D.4和1
6.如图△ABC中,∠C=90°,∠B=20°,以C为圆心,CA为半径的圆交AB于点D, 则的度数为( )
A.30° B.40° C.45° D.50°
7.已知三角形的两边长为3和6,第三边的长是方程的一个根,则这个三角形的周长是( )
A.12 B.13 C.12或13 D.15
8.x=1是关于x的一元二次方程x2+ax+2b=0的解,则﹣a﹣2b=( )
A.﹣1 B.1 C.2 D.﹣2
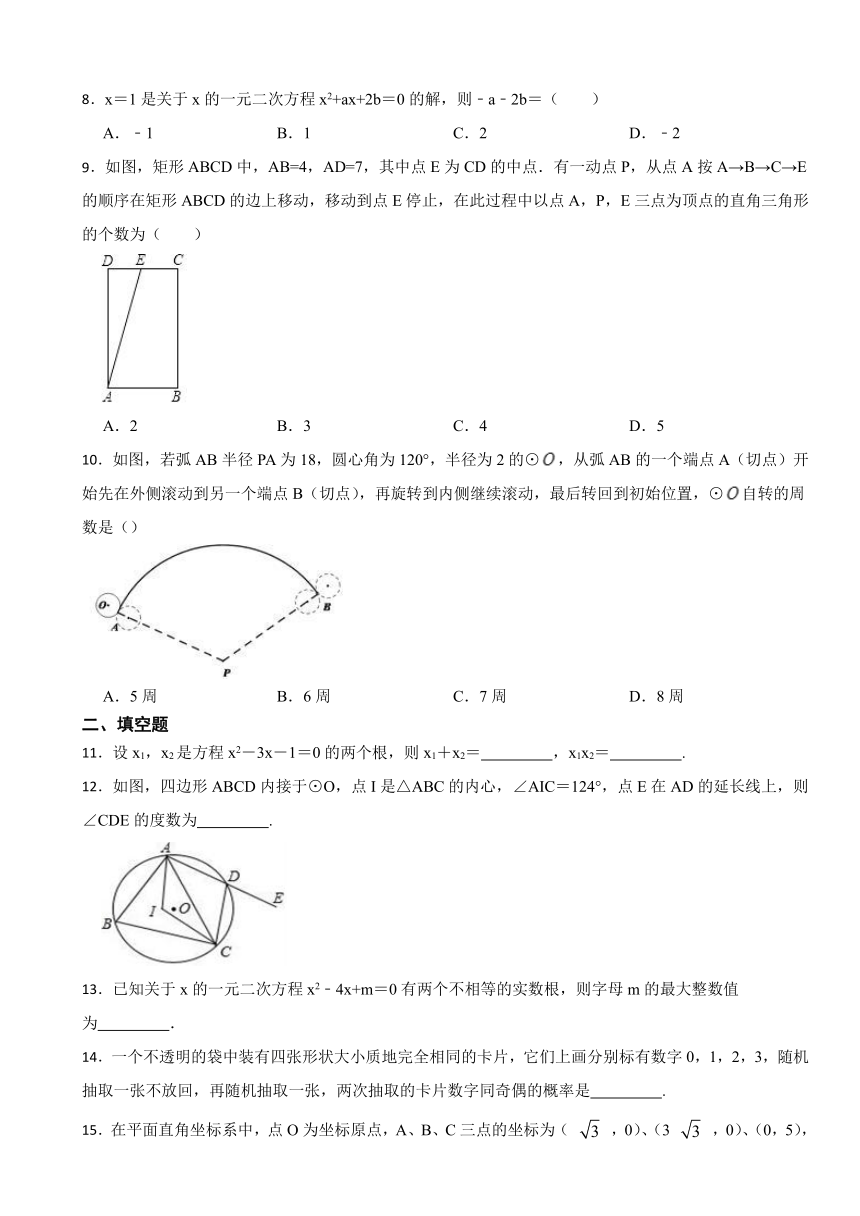
9.如图,矩形ABCD中,AB=4,AD=7,其中点E为CD的中点.有一动点P,从点A按A→B→C→E的顺序在矩形ABCD的边上移动,移动到点E停止,在此过程中以点A,P,E三点为顶点的直角三角形的个数为( )
A.2 B.3 C.4 D.5
10.如图,若弧AB半径PA为18,圆心角为120°,半径为2的⊙,从弧AB的一个端点A(切点)开始先在外侧滚动到另一个端点B(切点),再旋转到内侧继续滚动,最后转回到初始位置,⊙自转的周数是()
A.5周 B.6周 C.7周 D.8周
二、填空题
11.设x1,x2是方程x2-3x-1=0的两个根,则x1+x2= ,x1x2= .
12.如图,四边形ABCD内接于⊙O,点I是△ABC的内心,∠AIC=124°,点E在AD的延长线上,则∠CDE的度数为 .
13.已知关于x的一元二次方程x2﹣4x+m=0有两个不相等的实数根,则字母m的最大整数值为 .
14.一个不透明的袋中装有四张形状大小质地完全相同的卡片,它们上画分别标有数字0,1,2,3,随机抽取一张不放回,再随机抽取一张,两次抽取的卡片数字同奇偶的概率是 .
15.在平面直角坐标系中,点O为坐标原点,A、B、C三点的坐标为( ,0)、(3 ,0)、(0,5),点D在第一象限,且∠ADB=60°,则线段CD的长的最小值为 .
三、计算题
16.解方程:
(1)(x﹣5)(x﹣6)=x﹣5
(2)x2﹣4x+2=0.
四、解答题
17.如图所示,在△ABC中,CE,BD分别是AB,AC边上的高,求证:B,C,D,E四点在同一个圆上.
18.将方程 化为一元二次方程的一般式。
19.一些不便于直接测量的圆形孔道的直径可以用如下方法测量.如图,把一个直径为10mm的小钢球紧贴在孔道边缘,测得钢球顶端离孔道外端的距离为8mm.求这个孔道的直径AB.
20.将进货单价为40元的商品按50元售出,能售出500件,如果该商品涨价1元,其销售量就要减少10件,为了赚取8000元的利润,售价应定为多少元?这时应进货多少件?
21.已知方程 的一个根比另一个根小4,求这两个根和 的值.
22.阅读材料,解答问题:
为了解方程(x2﹣1)2﹣5(x2﹣1)+4=0,如果我们把x2﹣1看作一个整体,然后设x2﹣1=y…①,则原方程可化为y2﹣5y+4=0,易得y1=1,y2=4.
当y=1时,即:x2﹣1=1,∴x=±;
当y=4时,即:x2﹣1=4,∴x=±,
综上所求,原方程的解为:x1=,x2=﹣,x3=,x4=﹣.我们把以上这种解决问题的方法通常叫换元法,这种方法它体现了数学中复杂问题简单化、把未知化成已知的转化思想;请根据这种思想完成:直接应用:解方程x4﹣x2﹣6=0.
23.如图,在⊙O的内接四边形ABCD中,DB=DC,∠DAE是四边形ABCD的一个外角.∠DAE与∠DAC相等吗?为什么?
24.如图,在平面直角坐标系中,点O为坐标原点,直线y=﹣x+b与坐标轴交于C,D两点,直线AB与坐标轴交于A,B两点,线段OA,OC的长是方程x2﹣3x+2=0的两个根(OA>OC).
(1)求点A,C的坐标;
(2)直线AB与直线CD交于点E,若点E是线段AB的中点,反比例函数y= (k≠0)的图象的一个分支经过点E,求k的值;
(3)在(2)的条件下,点M在直线CD上,坐标平面内是否存在点N,使以点B,E,M,N为顶点的四边形是菱形?若存在,请直接写出满足条件的点N的坐标;若不存在,请说明理由.
一、单选题
1.某班10名学生的校服尺寸与对应人数如表所示:
尺寸(cm) 160 165 170 175 180
学生人数(人) 1 3 2 2 2
则这10名学生校服尺寸的众数和中位数分别为( )
A.165cm,165cm B.165cm,170cm C.170cm,165cm D.170cm,170cm
2.某兴趣小组为了解我市气温变化情况,记录了今年月份连续6天的最低气温(单位:℃): ,关于这组数据,下列结论不正确的是( )
A.平均数是 B.中位数是
C.众数是 D.方差是
3.一元二次方程x2-5x+6=0的 解为( )
A.X1=2,x2= -3 B.x1= -2, x2=-3
C.x1=-2,x2=-3 D.x1=2,x2=3
4.淘淘和丽丽是九年级学生,在5月份进行的物理、化学、生物实验技能考试中,考试科目要求三选一,并且采取抽签方式取得,那么他们两人都抽到物理实验的概率是( )
A. B. C. D.
5.已知关于x的方程(2x-m)(mx+1)=(3x+1)(mx-1)有一个根是0,则它的另一个根和m的值分别是( )
A.3和1 B.2和3 C.3和4 D.4和1
6.如图△ABC中,∠C=90°,∠B=20°,以C为圆心,CA为半径的圆交AB于点D, 则的度数为( )
A.30° B.40° C.45° D.50°
7.已知三角形的两边长为3和6,第三边的长是方程的一个根,则这个三角形的周长是( )
A.12 B.13 C.12或13 D.15
8.x=1是关于x的一元二次方程x2+ax+2b=0的解,则﹣a﹣2b=( )
A.﹣1 B.1 C.2 D.﹣2
9.如图,矩形ABCD中,AB=4,AD=7,其中点E为CD的中点.有一动点P,从点A按A→B→C→E的顺序在矩形ABCD的边上移动,移动到点E停止,在此过程中以点A,P,E三点为顶点的直角三角形的个数为( )
A.2 B.3 C.4 D.5
10.如图,若弧AB半径PA为18,圆心角为120°,半径为2的⊙,从弧AB的一个端点A(切点)开始先在外侧滚动到另一个端点B(切点),再旋转到内侧继续滚动,最后转回到初始位置,⊙自转的周数是()
A.5周 B.6周 C.7周 D.8周
二、填空题
11.设x1,x2是方程x2-3x-1=0的两个根,则x1+x2= ,x1x2= .
12.如图,四边形ABCD内接于⊙O,点I是△ABC的内心,∠AIC=124°,点E在AD的延长线上,则∠CDE的度数为 .
13.已知关于x的一元二次方程x2﹣4x+m=0有两个不相等的实数根,则字母m的最大整数值为 .
14.一个不透明的袋中装有四张形状大小质地完全相同的卡片,它们上画分别标有数字0,1,2,3,随机抽取一张不放回,再随机抽取一张,两次抽取的卡片数字同奇偶的概率是 .
15.在平面直角坐标系中,点O为坐标原点,A、B、C三点的坐标为( ,0)、(3 ,0)、(0,5),点D在第一象限,且∠ADB=60°,则线段CD的长的最小值为 .
三、计算题
16.解方程:
(1)(x﹣5)(x﹣6)=x﹣5
(2)x2﹣4x+2=0.
四、解答题
17.如图所示,在△ABC中,CE,BD分别是AB,AC边上的高,求证:B,C,D,E四点在同一个圆上.
18.将方程 化为一元二次方程的一般式。
19.一些不便于直接测量的圆形孔道的直径可以用如下方法测量.如图,把一个直径为10mm的小钢球紧贴在孔道边缘,测得钢球顶端离孔道外端的距离为8mm.求这个孔道的直径AB.
20.将进货单价为40元的商品按50元售出,能售出500件,如果该商品涨价1元,其销售量就要减少10件,为了赚取8000元的利润,售价应定为多少元?这时应进货多少件?
21.已知方程 的一个根比另一个根小4,求这两个根和 的值.
22.阅读材料,解答问题:
为了解方程(x2﹣1)2﹣5(x2﹣1)+4=0,如果我们把x2﹣1看作一个整体,然后设x2﹣1=y…①,则原方程可化为y2﹣5y+4=0,易得y1=1,y2=4.
当y=1时,即:x2﹣1=1,∴x=±;
当y=4时,即:x2﹣1=4,∴x=±,
综上所求,原方程的解为:x1=,x2=﹣,x3=,x4=﹣.我们把以上这种解决问题的方法通常叫换元法,这种方法它体现了数学中复杂问题简单化、把未知化成已知的转化思想;请根据这种思想完成:直接应用:解方程x4﹣x2﹣6=0.
23.如图,在⊙O的内接四边形ABCD中,DB=DC,∠DAE是四边形ABCD的一个外角.∠DAE与∠DAC相等吗?为什么?
24.如图,在平面直角坐标系中,点O为坐标原点,直线y=﹣x+b与坐标轴交于C,D两点,直线AB与坐标轴交于A,B两点,线段OA,OC的长是方程x2﹣3x+2=0的两个根(OA>OC).
(1)求点A,C的坐标;
(2)直线AB与直线CD交于点E,若点E是线段AB的中点,反比例函数y= (k≠0)的图象的一个分支经过点E,求k的值;
(3)在(2)的条件下,点M在直线CD上,坐标平面内是否存在点N,使以点B,E,M,N为顶点的四边形是菱形?若存在,请直接写出满足条件的点N的坐标;若不存在,请说明理由.
同课章节目录
