苏科版九年级下6.4探索三角形相似的条件(4)同步练习及答案
文档属性
| 名称 | 苏科版九年级下6.4探索三角形相似的条件(4)同步练习及答案 |
|
|
| 格式 | zip | ||
| 文件大小 | 78.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-05-22 00:00:00 | ||
图片预览

文档简介
第7课时 探索三角形相似的条件(4)
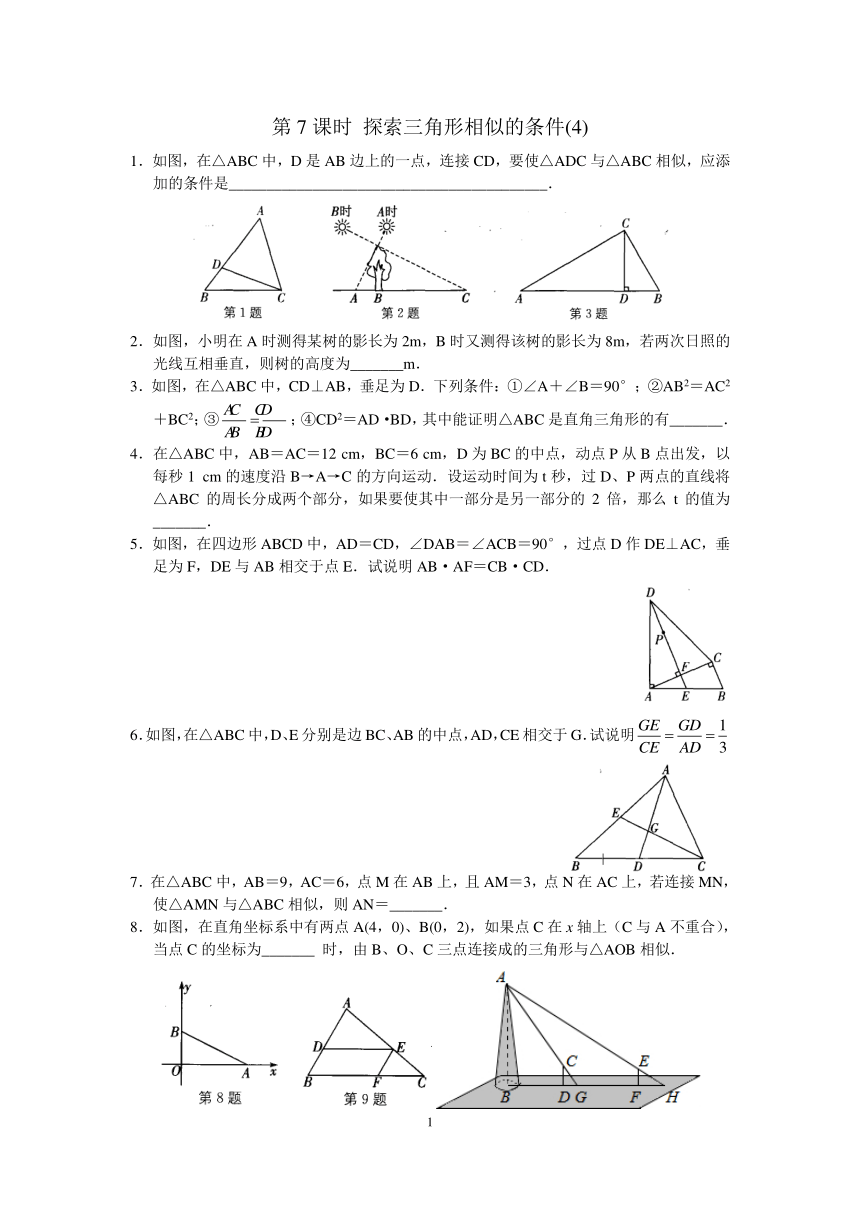
1.如图,在△ABC中,D是AB边上的一点,连接CD,要使△ADC与△ABC相似,应添加的条件是__________________________________________.
2.如图,小明在A时测得某树的影长为2m,B时又测得该树的影长为8m,若两次日照的光线互相垂直,则树的高度为_______m.
3.如图,在△ABC中,CD⊥AB,垂足为D.下列条件:①∠A+∠B=90°;②AB2=AC2+BC2;③;④CD2=AD·BD,其中能证明△ABC是直角三角形的有_______.
4.在△ABC中,AB=AC=12 cm,BC=6 cm,D为BC的中点,动点P从B点出发,以每秒1 cm的速度沿B→A→C的方向运动.设运动时间为t秒,过D、P两点的直线将△ABC的周长分成两个部分,如果要使其中一部分是另一部分的2倍,那么t的值为_______.
5.如图,在四边形ABCD中,AD=CD,∠DAB=∠ACB=90°,过点D作DE⊥AC,垂足为F,DE与AB相交于点E.试说明AB·AF=CB·CD.
6.如图,在△ABC中,D、E分别是边BC、AB的中点,AD,CE相交于G.试说明
7.在△ABC中,AB=9,AC=6,点M在AB上,且AM=3,点N在AC上,若连接MN,使△AMN与△ABC相似,则AN=_______.
8.如图,在直角坐标系中有两点A(4,0)、B(0,2),如果点C在x轴上(C与A不重合),当点C的坐标为_______ 时,由B、O、C三点连接成的三角形与△AOB相似.
9.如图,DE∥BC,EF∥AB,则下列比例式错误的是 ( )
A. B. C. D.
10.(2014潍坊)如图,某水平地面上建筑物的高度为AB,在点D和点F处分别竖立高是2米的CD和EF,两标杆相隔52米,并且建筑物AB、标杆CD和EF在同一竖直平面内,从标杆CD后退2米到点G处,在G处测得建筑物顶端A和标杆顶端C在同一条直线上;从标杆FE后退4米到点H处,在H处测得建筑物顶端A和标杆顶端E在同一条直线上,则建筑物的高是 米.
11.如图,在△ABC中,AD⊥BC,垂足为D,EC⊥AB,垂足为E,连接DE.试说明△BDE∽△BAC.
12.如图,在△ABC中,CD⊥AB,DE⊥AC,DF⊥BC,垂足分别为D、E、F.
(1) CA·CE与CB·CF相等吗?为什么?
(2)连接EF,交CD于点O,线段OC、OF、OE、OD成比例吗?
13.如图,AB⊥BD,CD⊥BD,AB=6 cm,CD=4 cm,BD=14 cm,点P在BD上由点B向点D方向移动,当点P移到离点B多远时,△APB和△CPD相似?
14.(2014.玉林)如图,在正方形ABCD中,点M是BC边上的任一点,连接AM并将线段AM绕M顺时针旋转90°得到线段MN,在CD边上取点P使CP=BM,连接NP,BP.
(1)求证:四边形BMNP是平行四边形;
(2)线段MN与CD交于点Q,连接AQ,若△MCQ∽△AMQ,则BM与MC存在怎样的数量关系?请说明理由.
参考答案
1.∠ACD=∠B或∠ADC=∠ACB或 2.4 3.①②④ 4.7或17
5.略 6.略
7.2或4.5 8.(-4,0)或(1,0)或(-1,0) 9.C 10.54 11.略
12.(1)相等 (2)成比例
13.8.4 cm或12 cm或2 cm
14.(1)证明:在正方形ABCD中,AB=BC,∠ABC=∠B,
在△ABM和△BCP中,
,
∴△ABM≌△BCP(SAS),
∴AM=BP,∠BAM=∠CBP,
∵∠BAM+∠AMB=90°,
∴∠CBP+∠AMB=90°,
∴AM⊥BP,
∵AM并将线段AM绕M顺时针旋转90°得到线段MN,
∴AM⊥MN,且AM=MN,
∴MN∥BP,
∴四边形BMNP是平行四边形;
(2)解:BM=MC.
理由如下:∵∠BAM+∠AMB=90°,∠AMB+∠CMQ=90°,
∴∠BAM=∠CMQ,
又∵∠B=∠C=90°,
∴△ABM∽△MCQ,
∴=,
∵△MCQ∽△AMQ,
∴△AMQ∽△ABM,
∴=, ∴=,
∴BM=MC.
1
1.如图,在△ABC中,D是AB边上的一点,连接CD,要使△ADC与△ABC相似,应添加的条件是__________________________________________.
2.如图,小明在A时测得某树的影长为2m,B时又测得该树的影长为8m,若两次日照的光线互相垂直,则树的高度为_______m.
3.如图,在△ABC中,CD⊥AB,垂足为D.下列条件:①∠A+∠B=90°;②AB2=AC2+BC2;③;④CD2=AD·BD,其中能证明△ABC是直角三角形的有_______.
4.在△ABC中,AB=AC=12 cm,BC=6 cm,D为BC的中点,动点P从B点出发,以每秒1 cm的速度沿B→A→C的方向运动.设运动时间为t秒,过D、P两点的直线将△ABC的周长分成两个部分,如果要使其中一部分是另一部分的2倍,那么t的值为_______.
5.如图,在四边形ABCD中,AD=CD,∠DAB=∠ACB=90°,过点D作DE⊥AC,垂足为F,DE与AB相交于点E.试说明AB·AF=CB·CD.
6.如图,在△ABC中,D、E分别是边BC、AB的中点,AD,CE相交于G.试说明
7.在△ABC中,AB=9,AC=6,点M在AB上,且AM=3,点N在AC上,若连接MN,使△AMN与△ABC相似,则AN=_______.
8.如图,在直角坐标系中有两点A(4,0)、B(0,2),如果点C在x轴上(C与A不重合),当点C的坐标为_______ 时,由B、O、C三点连接成的三角形与△AOB相似.
9.如图,DE∥BC,EF∥AB,则下列比例式错误的是 ( )
A. B. C. D.
10.(2014潍坊)如图,某水平地面上建筑物的高度为AB,在点D和点F处分别竖立高是2米的CD和EF,两标杆相隔52米,并且建筑物AB、标杆CD和EF在同一竖直平面内,从标杆CD后退2米到点G处,在G处测得建筑物顶端A和标杆顶端C在同一条直线上;从标杆FE后退4米到点H处,在H处测得建筑物顶端A和标杆顶端E在同一条直线上,则建筑物的高是 米.
11.如图,在△ABC中,AD⊥BC,垂足为D,EC⊥AB,垂足为E,连接DE.试说明△BDE∽△BAC.
12.如图,在△ABC中,CD⊥AB,DE⊥AC,DF⊥BC,垂足分别为D、E、F.
(1) CA·CE与CB·CF相等吗?为什么?
(2)连接EF,交CD于点O,线段OC、OF、OE、OD成比例吗?
13.如图,AB⊥BD,CD⊥BD,AB=6 cm,CD=4 cm,BD=14 cm,点P在BD上由点B向点D方向移动,当点P移到离点B多远时,△APB和△CPD相似?
14.(2014.玉林)如图,在正方形ABCD中,点M是BC边上的任一点,连接AM并将线段AM绕M顺时针旋转90°得到线段MN,在CD边上取点P使CP=BM,连接NP,BP.
(1)求证:四边形BMNP是平行四边形;
(2)线段MN与CD交于点Q,连接AQ,若△MCQ∽△AMQ,则BM与MC存在怎样的数量关系?请说明理由.
参考答案
1.∠ACD=∠B或∠ADC=∠ACB或 2.4 3.①②④ 4.7或17
5.略 6.略
7.2或4.5 8.(-4,0)或(1,0)或(-1,0) 9.C 10.54 11.略
12.(1)相等 (2)成比例
13.8.4 cm或12 cm或2 cm
14.(1)证明:在正方形ABCD中,AB=BC,∠ABC=∠B,
在△ABM和△BCP中,
,
∴△ABM≌△BCP(SAS),
∴AM=BP,∠BAM=∠CBP,
∵∠BAM+∠AMB=90°,
∴∠CBP+∠AMB=90°,
∴AM⊥BP,
∵AM并将线段AM绕M顺时针旋转90°得到线段MN,
∴AM⊥MN,且AM=MN,
∴MN∥BP,
∴四边形BMNP是平行四边形;
(2)解:BM=MC.
理由如下:∵∠BAM+∠AMB=90°,∠AMB+∠CMQ=90°,
∴∠BAM=∠CMQ,
又∵∠B=∠C=90°,
∴△ABM∽△MCQ,
∴=,
∵△MCQ∽△AMQ,
∴△AMQ∽△ABM,
∴=, ∴=,
∴BM=MC.
1
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
