天津市重点中学2023-2024学年高一上学期12月过程性诊断数学试卷(2)(含答案)
文档属性
| 名称 | 天津市重点中学2023-2024学年高一上学期12月过程性诊断数学试卷(2)(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 581.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-27 00:00:00 | ||
图片预览




文档简介
天津市第一百中学2023—2024学年第一学期过程性诊断(2)
高一数学
本试卷满分150分,考试用时120分钟。
一、单选题(每小题5分,共45分)
1.向量,,,则( )
A.9 B.3 C.1 D.
2.已知直线与圆交于,两点,则线段的长度为( )
A. B.2 C. D.
3.已知抛物线上一点的纵坐标为2,则点到抛物线焦点的距离为
A.2 B.3 C.4 D.5
4.已知直线:与:平行,则的值是( )
A.5 B.0或5 C.0 D.0或1
5.已知等比数列中,,且,那么=( )
A.31 B.32 C.63 D.64
6.在四面体中,,Q是的中点,且M为PQ的中点,若,,,则( ).
A. B.
C. D.
7.已知等差数列的前项和为,若,,则( )
A.40 B.70 C.90 D.100
8.在数列中,,(,),则( )
A.1 B. C. D.2
9.设双曲线的左、右焦点分别为、,离心率为e,过的直线与双曲线的右支交于A、B两点,若是以A为直角顶点的等腰直角三角形,则( )
A. B. C. D.
二、填空题(每小5分,共30分)
10.已知,若直线:与直线:相互垂直,则 .
11.已知圆与相交于A,B两点,则直线的方程是 .
12.已知等差数列的前n项和为,且,,则取最大值时, .
13.抛物线的焦点为,点为该抛物线上的动点,又已知定点,则的最小值是 .
14.已知直线与椭圆相交于两点,且线段的中点在直线上,则此椭圆的离心率为 .
15.若直线与曲线有公共点,则的取值范围是 .
三、解答题
16.(本题13分)
已知圆经过和两点,且圆心在直线上.
(1)求圆的方程;
(2)从点向圆C作切线,求切线方程.
17.(本题15分)
在各项均为正数的等比数列中,,且成等差数列.
(1)求等比数列的通项公式和前n项和;
(2)若数列满足,求数列的前项和的最大值.
(3)求数列的前项和
18.(本题15分)
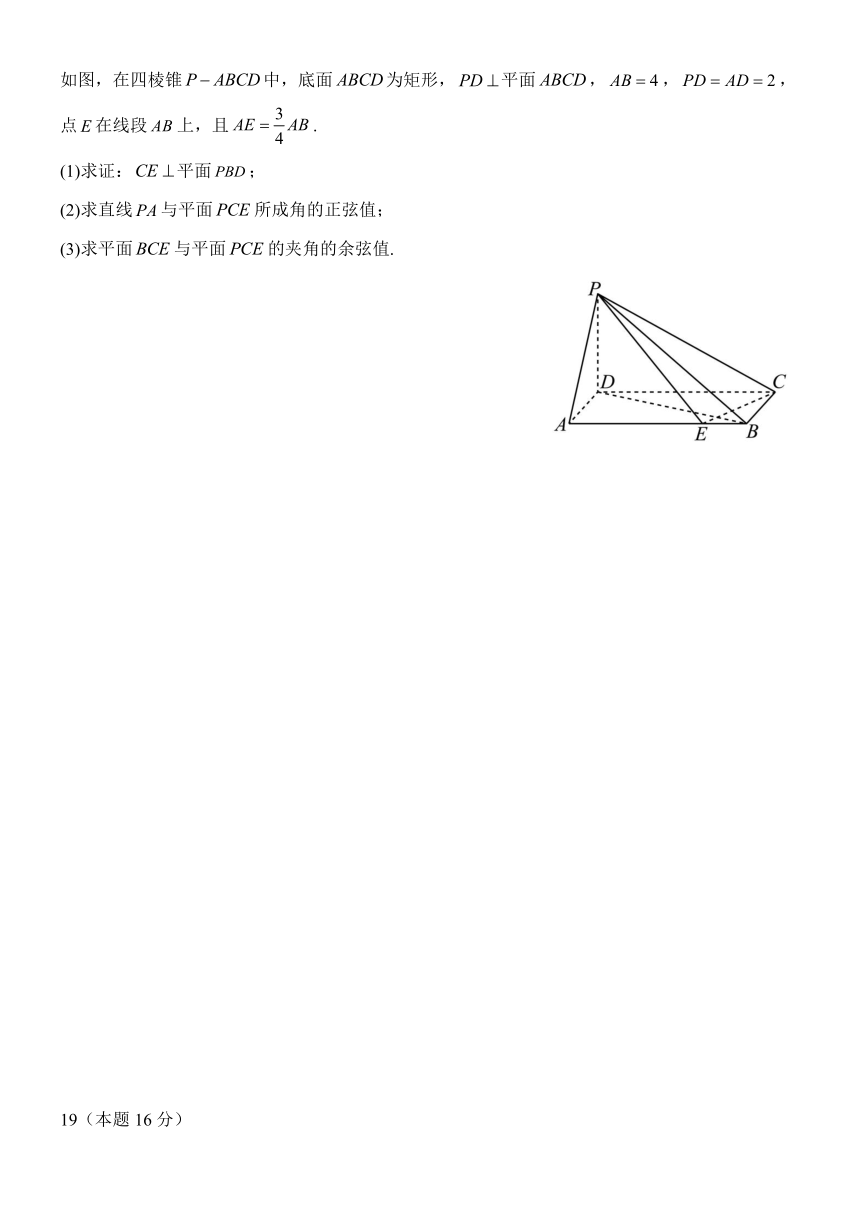
如图,在四棱锥中,底面为矩形,平面,,,点在线段上,且.
(1)求证:平面;
(2)求直线与平面所成角的正弦值;
(3)求平面与平面的夹角的余弦值.
19(本题16分)
已知正项数列的前项和为,且.
求数列的通项公式;
求数列前n项和
(3)若,数列的前项和为,求的取值范围;
20.(本题16分)
已知椭圆的离心率为,右焦点为.
(1)求椭圆方程;
(2)过点的直线与椭圆交于,两点,线段的垂直平分线与直线交于点,为等边三角形,求直线的方程
答案
一 、A C B C A D D B B
二 、10. ; 11.;12.15;13.;14.;15.。
三、
16..由题可知,所以线段的中垂线的斜率等于1,
又因为的中点为,
所以线段的中垂线的直线方程为,
即,
联立 解得 ,所以圆心
又因为半径等于,所以圆的方程为.....( 8分)
(2)设圆的半径为,则,
若直线的斜率不存在,因为直线过点,
所以直线方程为,.............................................................. (9分)
此时圆心到直线的距离,满足题意;
若直线的斜率存在,设斜率为,
则切线方程为,即,
因为直线与圆相切,所以圆心到直线的距离,(12分)
解得,...........................................................................(13分)
所以切线方程为,即.
所以切线方程为或................................(14分)
17.(1)设数列的公比为,
因为成等差数列,
所以......................................................1分
即,
所以,
解得或(舍去),................................4分
又,所以数列的通项公式..............5分
..................................................6分
(2)由题意得,,........................7分
则,且,
故数列是首项为9,公差为的等差数列,
所以,............9分
所以当时,的最大值为25.......................................10分
当时,,...............11分
当时,......13分
..................................................................15分
18.(1)证明:平面,平面,,,.
,,,,所以,又,
所以,,
,,,平面,平面...........5分
(2)平面,平面,平面,
,,为矩形,,
,,两两垂直,建立如图所示的空间直角坐标系,.............6分
则,,,,,,
,,,.........................................7分
设平面的法向量为,则,令,则,9分
设直线与平面所成角为,则,11分
所以直线与平面所成角的正弦值为.12分
(3)平面的一个法向量为,
设平面与平面的夹角为,
则,..........................14分
所以平面与平面的夹角的余弦值为.........................15分
19.(1)当时,由,得,得,...............2分
由,得,两式相减,得
,即,即
因为数列各项均为正数,所以,所以...............................5分
所以数列是以为首项,为公差的等差数列.
因此,,即数列的通项公式为............................7分
.....................................8分
两式相减得
...............................................................................................9分
..........................................................................................10分
(2)由(1)知,所以..........................11分
所以............12分
所以
..........................................................................................14分
令,则
所以是单调递增数列,数列递增,...............................................15分
所以,又,所以的取值范围为................................16分
20(1)由题意可得,,解得,.....................1分
由,∴..........................................................................2分
则椭圆的方程为...............................................................3分
(2)当直线为轴时,易得线段的垂直平分线与直线没有交点,故不满足题意;.....4分
当所在直线的斜率存在且不为轴时,设该直线方程为,,,
,解为,,..............................................................5分
所以,..........................................................7分
,................................8分
设的中点为,则,...............................................9分
设,
由为等边三角形,,,
,............................................11
..............13
所以,解得,所以,.................................14
当所在直线的斜率不存在时,将代入可得,
所以,,不满足题意,....................................................................15
综上所述,直线的方程为或...........................................................16
6
高一数学
本试卷满分150分,考试用时120分钟。
一、单选题(每小题5分,共45分)
1.向量,,,则( )
A.9 B.3 C.1 D.
2.已知直线与圆交于,两点,则线段的长度为( )
A. B.2 C. D.
3.已知抛物线上一点的纵坐标为2,则点到抛物线焦点的距离为
A.2 B.3 C.4 D.5
4.已知直线:与:平行,则的值是( )
A.5 B.0或5 C.0 D.0或1
5.已知等比数列中,,且,那么=( )
A.31 B.32 C.63 D.64
6.在四面体中,,Q是的中点,且M为PQ的中点,若,,,则( ).
A. B.
C. D.
7.已知等差数列的前项和为,若,,则( )
A.40 B.70 C.90 D.100
8.在数列中,,(,),则( )
A.1 B. C. D.2
9.设双曲线的左、右焦点分别为、,离心率为e,过的直线与双曲线的右支交于A、B两点,若是以A为直角顶点的等腰直角三角形,则( )
A. B. C. D.
二、填空题(每小5分,共30分)
10.已知,若直线:与直线:相互垂直,则 .
11.已知圆与相交于A,B两点,则直线的方程是 .
12.已知等差数列的前n项和为,且,,则取最大值时, .
13.抛物线的焦点为,点为该抛物线上的动点,又已知定点,则的最小值是 .
14.已知直线与椭圆相交于两点,且线段的中点在直线上,则此椭圆的离心率为 .
15.若直线与曲线有公共点,则的取值范围是 .
三、解答题
16.(本题13分)
已知圆经过和两点,且圆心在直线上.
(1)求圆的方程;
(2)从点向圆C作切线,求切线方程.
17.(本题15分)
在各项均为正数的等比数列中,,且成等差数列.
(1)求等比数列的通项公式和前n项和;
(2)若数列满足,求数列的前项和的最大值.
(3)求数列的前项和
18.(本题15分)
如图,在四棱锥中,底面为矩形,平面,,,点在线段上,且.
(1)求证:平面;
(2)求直线与平面所成角的正弦值;
(3)求平面与平面的夹角的余弦值.
19(本题16分)
已知正项数列的前项和为,且.
求数列的通项公式;
求数列前n项和
(3)若,数列的前项和为,求的取值范围;
20.(本题16分)
已知椭圆的离心率为,右焦点为.
(1)求椭圆方程;
(2)过点的直线与椭圆交于,两点,线段的垂直平分线与直线交于点,为等边三角形,求直线的方程
答案
一 、A C B C A D D B B
二 、10. ; 11.;12.15;13.;14.;15.。
三、
16..由题可知,所以线段的中垂线的斜率等于1,
又因为的中点为,
所以线段的中垂线的直线方程为,
即,
联立 解得 ,所以圆心
又因为半径等于,所以圆的方程为.....( 8分)
(2)设圆的半径为,则,
若直线的斜率不存在,因为直线过点,
所以直线方程为,.............................................................. (9分)
此时圆心到直线的距离,满足题意;
若直线的斜率存在,设斜率为,
则切线方程为,即,
因为直线与圆相切,所以圆心到直线的距离,(12分)
解得,...........................................................................(13分)
所以切线方程为,即.
所以切线方程为或................................(14分)
17.(1)设数列的公比为,
因为成等差数列,
所以......................................................1分
即,
所以,
解得或(舍去),................................4分
又,所以数列的通项公式..............5分
..................................................6分
(2)由题意得,,........................7分
则,且,
故数列是首项为9,公差为的等差数列,
所以,............9分
所以当时,的最大值为25.......................................10分
当时,,...............11分
当时,......13分
..................................................................15分
18.(1)证明:平面,平面,,,.
,,,,所以,又,
所以,,
,,,平面,平面...........5分
(2)平面,平面,平面,
,,为矩形,,
,,两两垂直,建立如图所示的空间直角坐标系,.............6分
则,,,,,,
,,,.........................................7分
设平面的法向量为,则,令,则,9分
设直线与平面所成角为,则,11分
所以直线与平面所成角的正弦值为.12分
(3)平面的一个法向量为,
设平面与平面的夹角为,
则,..........................14分
所以平面与平面的夹角的余弦值为.........................15分
19.(1)当时,由,得,得,...............2分
由,得,两式相减,得
,即,即
因为数列各项均为正数,所以,所以...............................5分
所以数列是以为首项,为公差的等差数列.
因此,,即数列的通项公式为............................7分
.....................................8分
两式相减得
...............................................................................................9分
..........................................................................................10分
(2)由(1)知,所以..........................11分
所以............12分
所以
..........................................................................................14分
令,则
所以是单调递增数列,数列递增,...............................................15分
所以,又,所以的取值范围为................................16分
20(1)由题意可得,,解得,.....................1分
由,∴..........................................................................2分
则椭圆的方程为...............................................................3分
(2)当直线为轴时,易得线段的垂直平分线与直线没有交点,故不满足题意;.....4分
当所在直线的斜率存在且不为轴时,设该直线方程为,,,
,解为,,..............................................................5分
所以,..........................................................7分
,................................8分
设的中点为,则,...............................................9分
设,
由为等边三角形,,,
,............................................11
..............13
所以,解得,所以,.................................14
当所在直线的斜率不存在时,将代入可得,
所以,,不满足题意,....................................................................15
综上所述,直线的方程为或...........................................................16
6
同课章节目录
