相似三角形的性质
图片预览



文档简介
课件30张PPT。相似三角形的性质课前复习:(1)什么叫相似三角形?
对应角相等、对应边成比例的三角形,叫做相似三角形.(2)如何判定两个三角形相似?①两个角对应相等;
②两边对应成比例,且夹角相等;
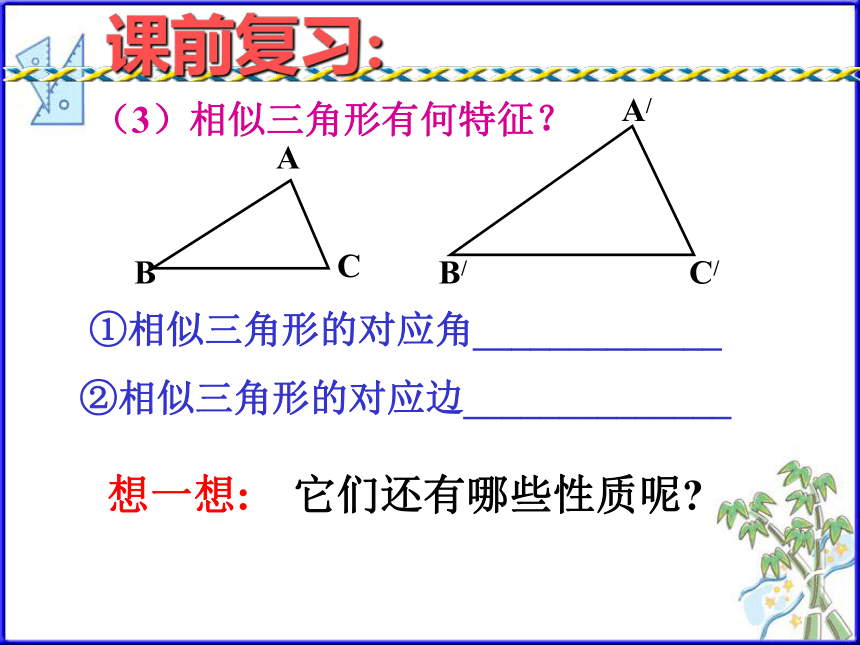
③三边对应成比例.ABCA/B/C/ ①相似三角形的对应角_____________
②相似三角形的对应边______________想一想: 它们还有哪些性质呢?课前复习:(3)相似三角形有何特征?一个三角形有三条重要线段:
________________如果两个三角形相似,
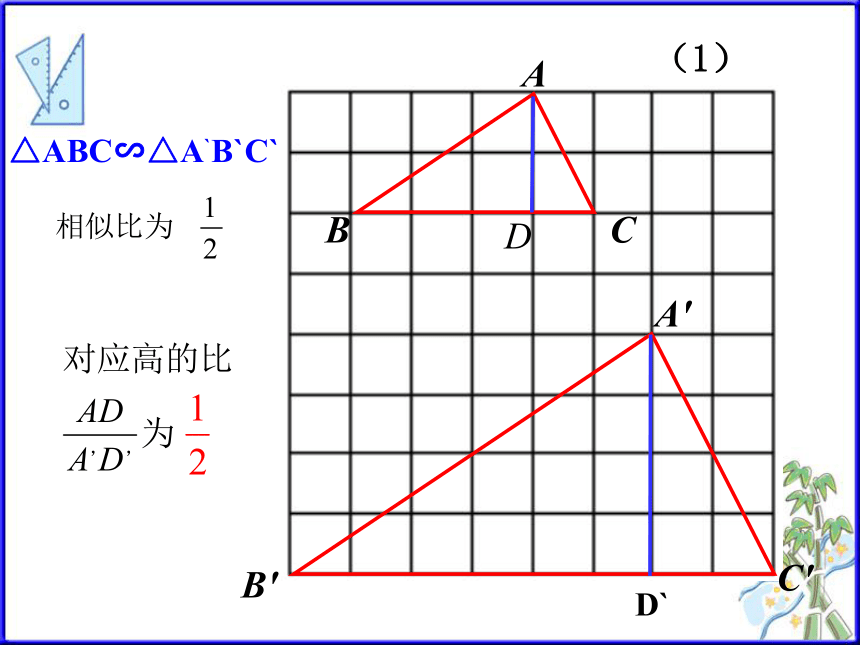
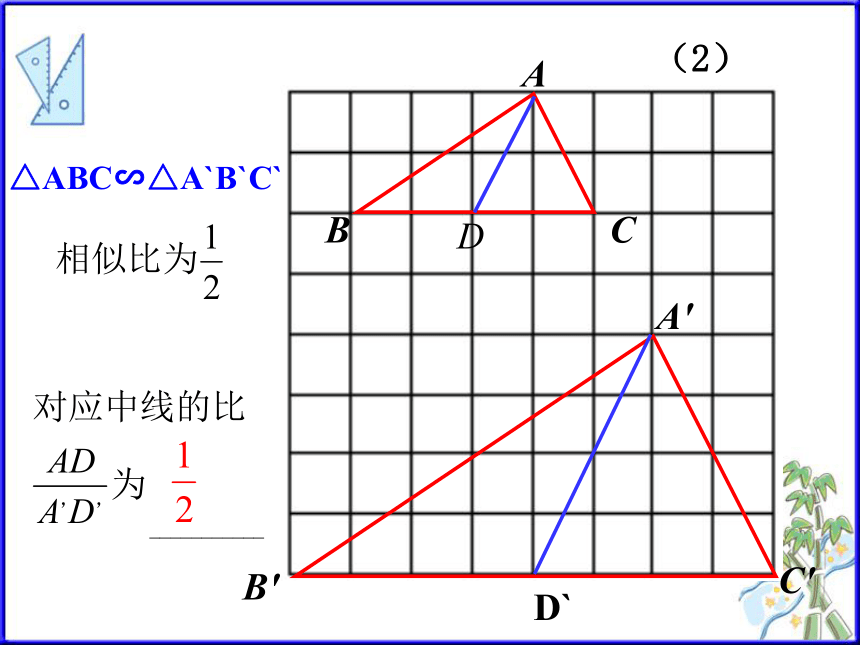
那么这些对应线段有什么关系呢?情境引入高、中线、角平分线(1)△ABC∽△A`B`C`D`(2)△ABC∽△A`B`C`
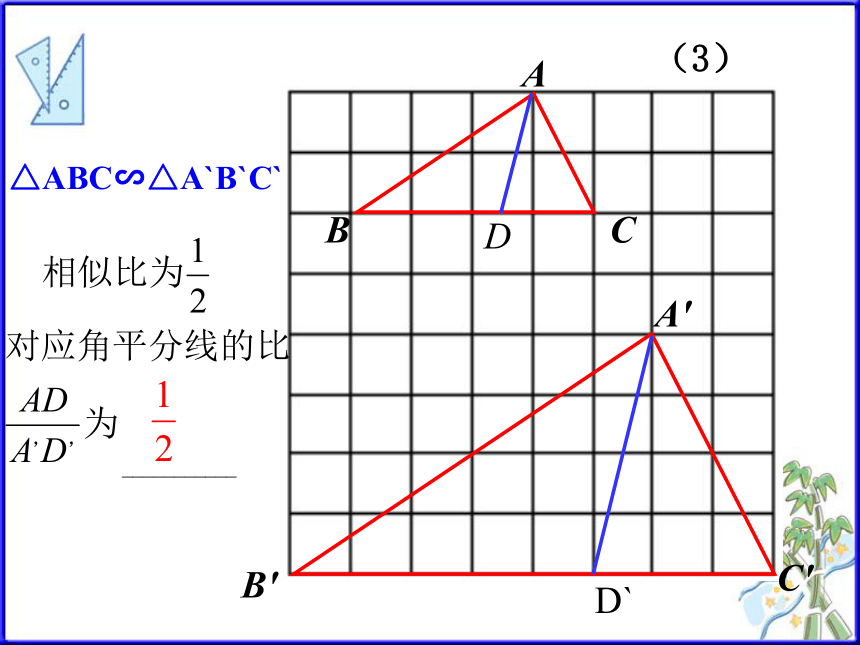
D`(3)△ABC∽△A`B`C`
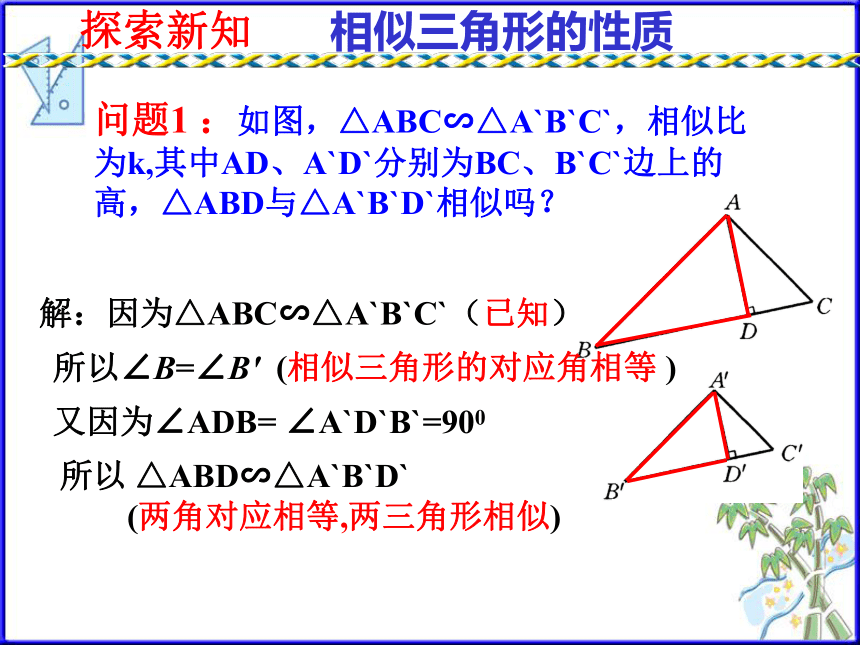
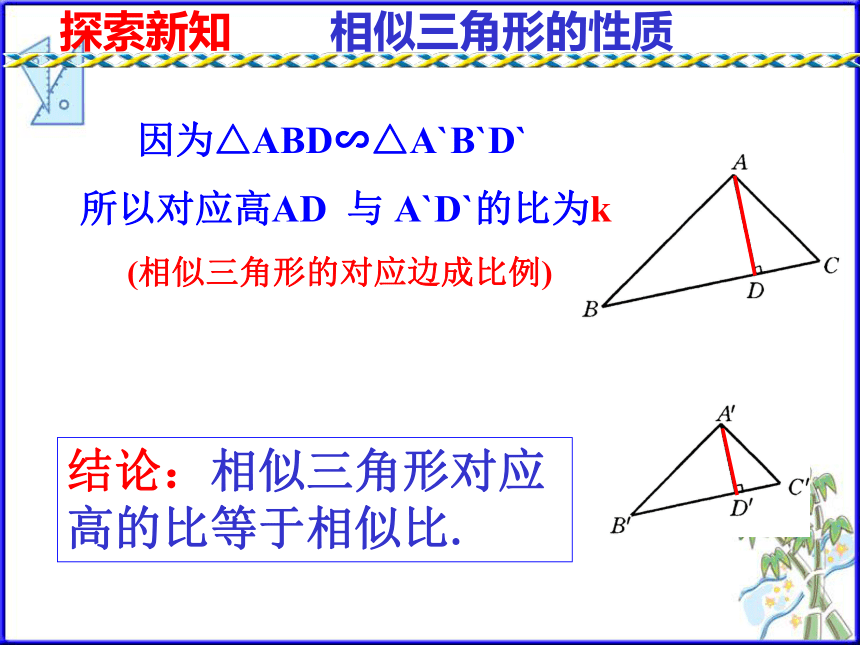
D`探索新知(两角对应相等,两三角形相似)问题1 :如图,△ABC∽△A`B`C`,相似比为k,其中AD、A`D`分别为BC、B`C`边上的高,△ABD与△A`B`D`相似吗?所以∠B=∠B′ (相似三角形的对应角相等 ) 相似三角形的性质解:因为△ABC∽△A`B`C`(已知)又因为∠ADB= ∠A`D`B`=900所以 △ABD∽△A`B`D`探索新知(相似三角形的对应边成比例)相似三角形的性质结论:相似三角形对应高的比等于相似比. 因为△ABD∽△A`B`D`
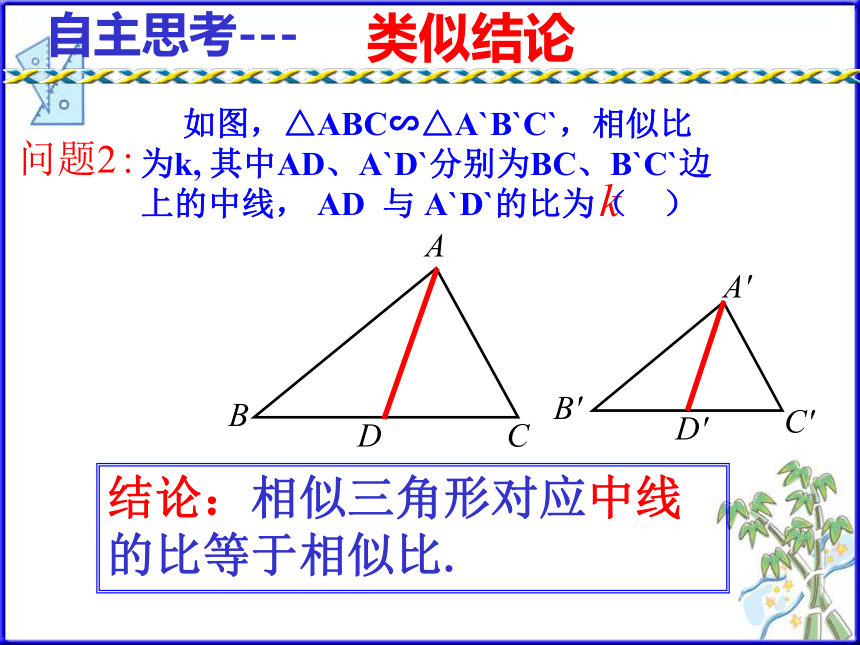
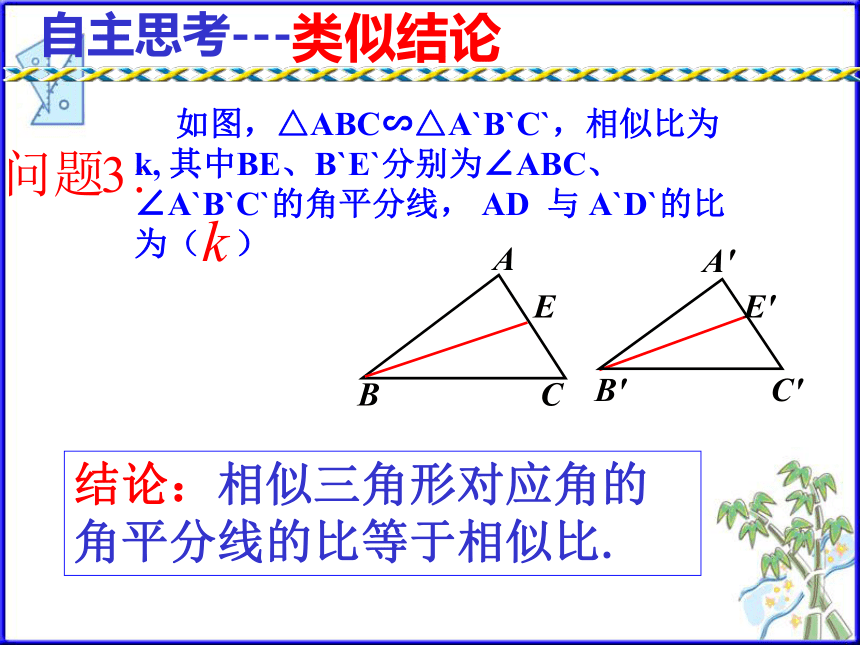
所以对应高AD 与 A`D`的比为k类似结论D'C'B'A'DCBA自主思考---结论:相似三角形对应中线的比等于相似比. 如图,△ABC∽△A`B`C`,相似比为k, 其中AD、A`D`分别为BC、B`C`边上的中线, AD 与 A`D`的比为( )A′C′B′CBAE′E类似结论自主思考---结论:相似三角形对应角的角平分线的比等于相似比. 如图,△ABC∽△A`B`C`,相似比为k, 其中BE、B`E`分别为∠ABC、 ∠A`B`C`的角平分线, AD 与 A`D`的比为( )
对应高的比
对应中线的比
对应角平分线的比 相
似
三
角
形都等于相似比.相似三角形的性质填一填1.相似三角形对应边的比为2∶3,那么相似比为_________,对应角的角平分线的比为______.2∶ 32 ∶ 32.两个相似三角形的相似比为0.25, 则对应高的比为_________,对应角的角平分线的比为_________. 0.250.25图中(1)(2)(3)分别是边长为1、2、3的等边三角形,它们都相似吗?(1)(2)(3)123用心观察(1)与(2)的相似比=______,
(1)与(2)的周长比=______
(2)与(3)的相似比=______,
(2)与(3)的周长比=______1∶ 2结论: 相似三角形的周长比等于______.相似比(都相似)2∶ 31∶ 22∶ 3对应高的比
对应中线的比
对应角平分线的比
周长的比 相
似
三
角
形都等于相似比.相似三角形的性质用心观察1231∶ 2当相似比=k时,面积比=k2. (1)(2)(3)(1)与(2)的相似比=______,
(1)与(2)的面积比=______
(2)与(3)的相似比=______,
(2)与(3)的面积比=______1∶ 42∶ 34∶ 9相似三角形面积的比等于相似比的平方.图中(1)(2)(3)分别是边长为1、2、3的等边三角形,它们都相似吗?(1)(2)(3)123用心观察(1)与(2)的相似比=______,
(1)与(2)的周长比=______
(2)与(3)的相似比=______,
(2)与(3)的周长比=______1∶ 2结论: 相似三角形的周长比等于______.相似比(都相似)2∶ 31∶ 22∶ 3对应高的比
对应中线的比
对应角平分线的比
周长的比 相
似
三
角
形都等于相似比.相似三角形的性质用心观察1231∶ 2当相似比=k时,面积比=k2. (1)(2)(3)(1)与(2)的相似比=______,
(1)与(2)的面积比=______
(2)与(3)的相似比=______,
(2)与(3)的面积比=______1∶ 42∶ 34∶ 9相似三角形面积的比等于相似比的平方.对应高的比
对应中线的比
对应角平分线的比
周长的比 相
似
三
角
形都等于相似比.面积的比等于相似比的平方相似三角形的性质运用性质,发展能力 (1)若两个的面积比为1:2,则他们的相似比为
(2)若△ABC~△A’B’C’,AB=5,A’B’=3, △A’B’C’的周长是12,则△ABC的周长是
如图所示:DE∥BC,AE:CE=2:1,试说明
S△DOE:S△BOC=4:9例1:例2:1.如果两个三角形相似,相似比为3∶5,则对应角的角平分线的比等于______.2.相似三角形对应边的比为0.4,
那么相似比为_______,
对应角的角平分线的比为______,
周长的比为_________,
面积的比为_________.3∶5 0.4当堂训练0.40.40.16当堂训练3.把一个三角形变成和它相似的三角形,
(1)如果边长扩大为原来的5倍,那么面积扩大为原来的__________倍。
(2)如果面积扩大为原来的100倍,那么边长扩大为原来的__________倍。
3,两个相似三角形的一对对应边分别是35厘米和14 厘米,(1)它们的周长差60厘米,这两个三角形的周长分别是________________。(2)它们的面积之和是58平方厘米,这两个三角形的面积分别是______________。2510100cm、40cm50cm2、40cm23.如图,在正方形网格上有△A1B1C1和△A2B2C2 ,这两个三角形相似吗?
如果相似,求出△A1B1C1和△A2B2C2的面积比.2 : 1解:相似.因为相似比是
所以面积比是4 : 1当堂训练 例3:已知△ABC∽ △A′B ′C ′,BD和B ′D ′分别是△ABC和△A′B′C′中线,且AB=10,A′B′=2,BD=6。求B′D′的长。
解:∵ △ABC∽△A′B′C′∴ == B′D′=1.2答:B′D′的长为1.2。 2004年五一黄金周期间青海省举办了盛大的郁金香节,吸引了许多外地游客前来观光。有一广东省旅游团来到西宁,还想去青海湖、塔尔寺两地旅游,在省地图册上:西宁、青海湖、塔尔寺构成的三角形周长约为7.5厘米,西宁至青海湖图距约有3厘米,而西宁至青海湖实际距离约有150千米,问从西宁—青海湖—塔尔寺—西宁实际距离之和约是多少千米? 例4: 1、相似三角形对应边成____,对应角______.
2、相似三角形对应边上的高、对应边上的中线、
对应角平分线的比都等于________.
3、相似三角形周长的比等于________,
相似三角形面积的比等于______________.
课堂小结相似比的平方相似三角形的性质相似多边形也有同样的结论1、已知两个等边三角形的边长之比为 2 :3,且它们的面积之和为26cm2,则较小的等边三角形的面积为多少?拓展训练布置作业: 1、必做:第93页第8题.
2、选作:自编一道涉及本节内容的实际问题,并
给出解答.(拓展题)
3、思考题:相似多边形也有同样的性质吗?
(探究题)谢谢!
对应角相等、对应边成比例的三角形,叫做相似三角形.(2)如何判定两个三角形相似?①两个角对应相等;
②两边对应成比例,且夹角相等;
③三边对应成比例.ABCA/B/C/ ①相似三角形的对应角_____________
②相似三角形的对应边______________想一想: 它们还有哪些性质呢?课前复习:(3)相似三角形有何特征?一个三角形有三条重要线段:
________________如果两个三角形相似,
那么这些对应线段有什么关系呢?情境引入高、中线、角平分线(1)△ABC∽△A`B`C`D`(2)△ABC∽△A`B`C`
D`(3)△ABC∽△A`B`C`
D`探索新知(两角对应相等,两三角形相似)问题1 :如图,△ABC∽△A`B`C`,相似比为k,其中AD、A`D`分别为BC、B`C`边上的高,△ABD与△A`B`D`相似吗?所以∠B=∠B′ (相似三角形的对应角相等 ) 相似三角形的性质解:因为△ABC∽△A`B`C`(已知)又因为∠ADB= ∠A`D`B`=900所以 △ABD∽△A`B`D`探索新知(相似三角形的对应边成比例)相似三角形的性质结论:相似三角形对应高的比等于相似比. 因为△ABD∽△A`B`D`
所以对应高AD 与 A`D`的比为k类似结论D'C'B'A'DCBA自主思考---结论:相似三角形对应中线的比等于相似比. 如图,△ABC∽△A`B`C`,相似比为k, 其中AD、A`D`分别为BC、B`C`边上的中线, AD 与 A`D`的比为( )A′C′B′CBAE′E类似结论自主思考---结论:相似三角形对应角的角平分线的比等于相似比. 如图,△ABC∽△A`B`C`,相似比为k, 其中BE、B`E`分别为∠ABC、 ∠A`B`C`的角平分线, AD 与 A`D`的比为( )
对应高的比
对应中线的比
对应角平分线的比 相
似
三
角
形都等于相似比.相似三角形的性质填一填1.相似三角形对应边的比为2∶3,那么相似比为_________,对应角的角平分线的比为______.2∶ 32 ∶ 32.两个相似三角形的相似比为0.25, 则对应高的比为_________,对应角的角平分线的比为_________. 0.250.25图中(1)(2)(3)分别是边长为1、2、3的等边三角形,它们都相似吗?(1)(2)(3)123用心观察(1)与(2)的相似比=______,
(1)与(2)的周长比=______
(2)与(3)的相似比=______,
(2)与(3)的周长比=______1∶ 2结论: 相似三角形的周长比等于______.相似比(都相似)2∶ 31∶ 22∶ 3对应高的比
对应中线的比
对应角平分线的比
周长的比 相
似
三
角
形都等于相似比.相似三角形的性质用心观察1231∶ 2当相似比=k时,面积比=k2. (1)(2)(3)(1)与(2)的相似比=______,
(1)与(2)的面积比=______
(2)与(3)的相似比=______,
(2)与(3)的面积比=______1∶ 42∶ 34∶ 9相似三角形面积的比等于相似比的平方.图中(1)(2)(3)分别是边长为1、2、3的等边三角形,它们都相似吗?(1)(2)(3)123用心观察(1)与(2)的相似比=______,
(1)与(2)的周长比=______
(2)与(3)的相似比=______,
(2)与(3)的周长比=______1∶ 2结论: 相似三角形的周长比等于______.相似比(都相似)2∶ 31∶ 22∶ 3对应高的比
对应中线的比
对应角平分线的比
周长的比 相
似
三
角
形都等于相似比.相似三角形的性质用心观察1231∶ 2当相似比=k时,面积比=k2. (1)(2)(3)(1)与(2)的相似比=______,
(1)与(2)的面积比=______
(2)与(3)的相似比=______,
(2)与(3)的面积比=______1∶ 42∶ 34∶ 9相似三角形面积的比等于相似比的平方.对应高的比
对应中线的比
对应角平分线的比
周长的比 相
似
三
角
形都等于相似比.面积的比等于相似比的平方相似三角形的性质运用性质,发展能力 (1)若两个的面积比为1:2,则他们的相似比为
(2)若△ABC~△A’B’C’,AB=5,A’B’=3, △A’B’C’的周长是12,则△ABC的周长是
如图所示:DE∥BC,AE:CE=2:1,试说明
S△DOE:S△BOC=4:9例1:例2:1.如果两个三角形相似,相似比为3∶5,则对应角的角平分线的比等于______.2.相似三角形对应边的比为0.4,
那么相似比为_______,
对应角的角平分线的比为______,
周长的比为_________,
面积的比为_________.3∶5 0.4当堂训练0.40.40.16当堂训练3.把一个三角形变成和它相似的三角形,
(1)如果边长扩大为原来的5倍,那么面积扩大为原来的__________倍。
(2)如果面积扩大为原来的100倍,那么边长扩大为原来的__________倍。
3,两个相似三角形的一对对应边分别是35厘米和14 厘米,(1)它们的周长差60厘米,这两个三角形的周长分别是________________。(2)它们的面积之和是58平方厘米,这两个三角形的面积分别是______________。2510100cm、40cm50cm2、40cm23.如图,在正方形网格上有△A1B1C1和△A2B2C2 ,这两个三角形相似吗?
如果相似,求出△A1B1C1和△A2B2C2的面积比.2 : 1解:相似.因为相似比是
所以面积比是4 : 1当堂训练 例3:已知△ABC∽ △A′B ′C ′,BD和B ′D ′分别是△ABC和△A′B′C′中线,且AB=10,A′B′=2,BD=6。求B′D′的长。
解:∵ △ABC∽△A′B′C′∴ == B′D′=1.2答:B′D′的长为1.2。 2004年五一黄金周期间青海省举办了盛大的郁金香节,吸引了许多外地游客前来观光。有一广东省旅游团来到西宁,还想去青海湖、塔尔寺两地旅游,在省地图册上:西宁、青海湖、塔尔寺构成的三角形周长约为7.5厘米,西宁至青海湖图距约有3厘米,而西宁至青海湖实际距离约有150千米,问从西宁—青海湖—塔尔寺—西宁实际距离之和约是多少千米? 例4: 1、相似三角形对应边成____,对应角______.
2、相似三角形对应边上的高、对应边上的中线、
对应角平分线的比都等于________.
3、相似三角形周长的比等于________,
相似三角形面积的比等于______________.
课堂小结相似比的平方相似三角形的性质相似多边形也有同样的结论1、已知两个等边三角形的边长之比为 2 :3,且它们的面积之和为26cm2,则较小的等边三角形的面积为多少?拓展训练布置作业: 1、必做:第93页第8题.
2、选作:自编一道涉及本节内容的实际问题,并
给出解答.(拓展题)
3、思考题:相似多边形也有同样的性质吗?
(探究题)谢谢!
