4.2.2等差数列的前n项和公式(第三课时) 课件(共20张PPT)
文档属性
| 名称 | 4.2.2等差数列的前n项和公式(第三课时) 课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 614.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-27 15:35:39 | ||
图片预览






文档简介
(共21张PPT)
4.2.2 等差数列的前n项和公式
(第三课时)
思考:我们发现,等差数列{an}的前n项和公式 可化简为 , 这个函数式与函数 有什么关系?
当d=0 时,Sn的图象是一条直线上的均匀分布的点.
当d≠0 时, 是二次函数
当x = n时的函数值.
几何意义:前n项和公式Sn的图象是一条过坐标原点的抛物线上
孤立的点.
常数列
探究新知
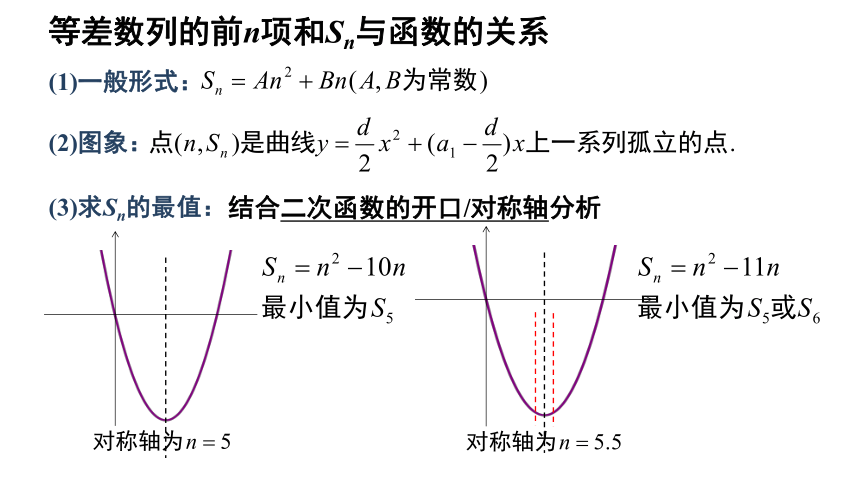
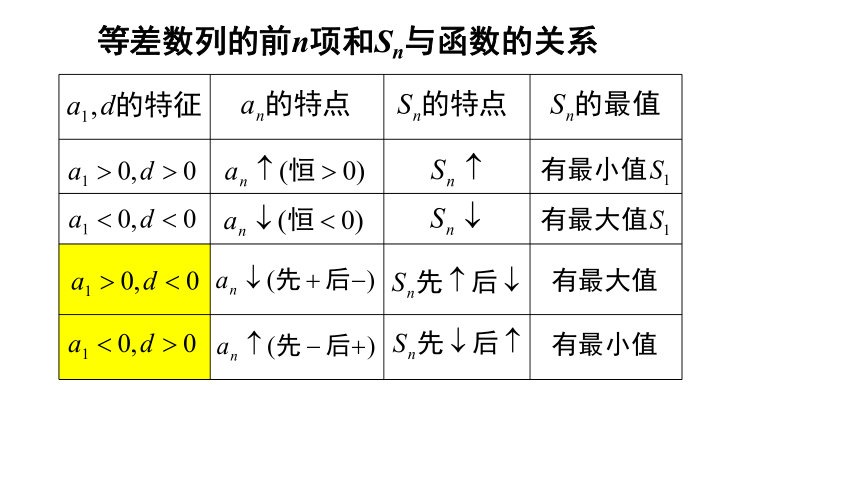
等差数列的前n项和Sn与函数的关系
(3)求Sn的最值:
(1)一般形式:
(2)图象:
结合二次函数的开口/对称轴分析
1.当a1<0,d>0 时,Sn的图象是一条开口向上
的过坐标原点的抛物线上孤立的点.
Sn
n
O
1
探究新知
方法2: 当a1<0,d>0时,数列前面有若干项为负, 此时所有负项的和为Sn的最小值.
方法1: 由 利用二次函数的对称轴,求得最值及取得最值时的n的值.
此时由an≤0 且an+1 ≥ 0求n的值
2.当a1>0,d<0 时,Sn的图象是一条开口向下的过坐标原点的抛物线上孤立的点.
Sn
n
O
1
探究新知
方法2: 当a1>0,d<0时,数列前面有若干项为正, 此时所有正项的和为Sn的最大值.
此时由an≥0且an+1≤0求n的值
方法1: 由 利用二次函数的对称轴,求得最值及取得最值时的n的值.
等差数列的前n项和Sn与函数的关系
例9 已知等差数列{an}的前n项和为Sn,若a1=10,公差d=-2,Sn是否存在最大值?若存在,求Sn的最大值及取得最大值时n的值;若不存在,请说明理由.
通项公式an的单调性求最值
解法1:
注意:当数列的项中有数值为0时,n应有两解.
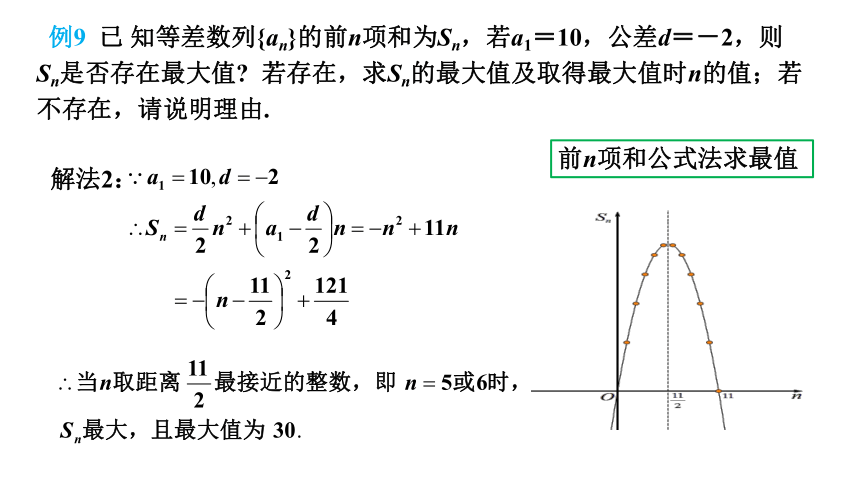
前n项和公式法求最值
解法2:
例9 已 知等差数列{an}的前n项和为Sn,若a1=10,公差d=-2,则Sn是否存在最大值 若存在,求Sn的最大值及取得最大值时n的值;若不存在,请说明理由.
(法1)
(法2)
利用二次函数的性质求Sn的最值
利用邻项异号求Sn的最值
(法3)
数形结合利用Sn的对称轴求Sn的最值
(法4)
利用等差数列的单调性求Sn的最值
1.已知等差数列{an}中, a1=13且S3=S11, 求n取何值时, Sn取最大值.
解法1:
由S3=S11, 得
∴ d=-2
故当n=7时, Sn取最大值49.
巩固练习
解法2:
由S3=S11, 得d=-2<0
则Sn的图象如下图所示
∴图象的对称轴为
故当n=7时, Sn取最大值49.
7
n
11
3
Sn
解法3:
∴an=13+(n-1) ×(-2)=-2n+15
由 ,
得
故当n=7时, Sn取最大值49.
由S3=S11, 得d=-2<0
∴a7+a8=0
a4+a5+a6+……+a11=0
而 a4+a11=a5+a10=a6+a9=a7+a8
又d=-2<0, a1=13>0
∴a7>0,a8<0
解法4:
由S3=S11, 得
故当n=7时, Sn取最大值49.
1.已知等差数列{an}中, a1=13且S3=S11, 求n取何值时, Sn取最大值.
巩固练习
练习2:在等差数列{an}中,若a1>0,S11=S18,则数列{an}的前_______项的和最大.
练习2:在等差数列{an}中,若a1>0,S11=S18,则数列{an}的前_______项的和最大.
求数列{|an|}的前n项和
方法小结:求数列{|an|}的前n项和
求数列{|an|}的前n项和,关键在于分清哪些项为正的,哪些项是负的,通过去绝对值,转化为数列{an}的前n项和问题.
3. 已知等差数列-4.2,-3.7,-3.2, 的前n项和为Sn,Sn是否存在最大(小)值 如果存在,求出取得最值时n的值.
课本P24
课本P24
(1)当a1>0,d<0时,数列前面有若干项为正, 此时所有正项的和为Sn的最大值. 此时由an≥0且an+1≤0求n的值;
(2)当a1<0,d>0时,数列前面有若干项为负, 此时所有负项的和为Sn的最小值. 此时由an≤0 且an+1 ≥ 0求n的值;
注意:当数列的项中有数值为0时,n应有两解.
求等差数列{an}的前n项和Sn的最值的方法
1.前n项和公式法
2.通项公式法
利用Sn=An2+Bn进行配方,求二次函数的最值,
此时n应取最接近 的正整数值;
利用等差数列的增减性及an的符号变化
课堂小结
求等差数列前n项和Sn的最大(小)值的常用方法
(1) 通项法
利用等差数列的单调性,求出an正负转折项,或者利用性质求其正负转折项.
等差数列前n项和的应用:
大
小
4.2.2 等差数列的前n项和公式
(第三课时)
思考:我们发现,等差数列{an}的前n项和公式 可化简为 , 这个函数式与函数 有什么关系?
当d=0 时,Sn的图象是一条直线上的均匀分布的点.
当d≠0 时, 是二次函数
当x = n时的函数值.
几何意义:前n项和公式Sn的图象是一条过坐标原点的抛物线上
孤立的点.
常数列
探究新知
等差数列的前n项和Sn与函数的关系
(3)求Sn的最值:
(1)一般形式:
(2)图象:
结合二次函数的开口/对称轴分析
1.当a1<0,d>0 时,Sn的图象是一条开口向上
的过坐标原点的抛物线上孤立的点.
Sn
n
O
1
探究新知
方法2: 当a1<0,d>0时,数列前面有若干项为负, 此时所有负项的和为Sn的最小值.
方法1: 由 利用二次函数的对称轴,求得最值及取得最值时的n的值.
此时由an≤0 且an+1 ≥ 0求n的值
2.当a1>0,d<0 时,Sn的图象是一条开口向下的过坐标原点的抛物线上孤立的点.
Sn
n
O
1
探究新知
方法2: 当a1>0,d<0时,数列前面有若干项为正, 此时所有正项的和为Sn的最大值.
此时由an≥0且an+1≤0求n的值
方法1: 由 利用二次函数的对称轴,求得最值及取得最值时的n的值.
等差数列的前n项和Sn与函数的关系
例9 已知等差数列{an}的前n项和为Sn,若a1=10,公差d=-2,Sn是否存在最大值?若存在,求Sn的最大值及取得最大值时n的值;若不存在,请说明理由.
通项公式an的单调性求最值
解法1:
注意:当数列的项中有数值为0时,n应有两解.
前n项和公式法求最值
解法2:
例9 已 知等差数列{an}的前n项和为Sn,若a1=10,公差d=-2,则Sn是否存在最大值 若存在,求Sn的最大值及取得最大值时n的值;若不存在,请说明理由.
(法1)
(法2)
利用二次函数的性质求Sn的最值
利用邻项异号求Sn的最值
(法3)
数形结合利用Sn的对称轴求Sn的最值
(法4)
利用等差数列的单调性求Sn的最值
1.已知等差数列{an}中, a1=13且S3=S11, 求n取何值时, Sn取最大值.
解法1:
由S3=S11, 得
∴ d=-2
故当n=7时, Sn取最大值49.
巩固练习
解法2:
由S3=S11, 得d=-2<0
则Sn的图象如下图所示
∴图象的对称轴为
故当n=7时, Sn取最大值49.
7
n
11
3
Sn
解法3:
∴an=13+(n-1) ×(-2)=-2n+15
由 ,
得
故当n=7时, Sn取最大值49.
由S3=S11, 得d=-2<0
∴a7+a8=0
a4+a5+a6+……+a11=0
而 a4+a11=a5+a10=a6+a9=a7+a8
又d=-2<0, a1=13>0
∴a7>0,a8<0
解法4:
由S3=S11, 得
故当n=7时, Sn取最大值49.
1.已知等差数列{an}中, a1=13且S3=S11, 求n取何值时, Sn取最大值.
巩固练习
练习2:在等差数列{an}中,若a1>0,S11=S18,则数列{an}的前_______项的和最大.
练习2:在等差数列{an}中,若a1>0,S11=S18,则数列{an}的前_______项的和最大.
求数列{|an|}的前n项和
方法小结:求数列{|an|}的前n项和
求数列{|an|}的前n项和,关键在于分清哪些项为正的,哪些项是负的,通过去绝对值,转化为数列{an}的前n项和问题.
3. 已知等差数列-4.2,-3.7,-3.2, 的前n项和为Sn,Sn是否存在最大(小)值 如果存在,求出取得最值时n的值.
课本P24
课本P24
(1)当a1>0,d<0时,数列前面有若干项为正, 此时所有正项的和为Sn的最大值. 此时由an≥0且an+1≤0求n的值;
(2)当a1<0,d>0时,数列前面有若干项为负, 此时所有负项的和为Sn的最小值. 此时由an≤0 且an+1 ≥ 0求n的值;
注意:当数列的项中有数值为0时,n应有两解.
求等差数列{an}的前n项和Sn的最值的方法
1.前n项和公式法
2.通项公式法
利用Sn=An2+Bn进行配方,求二次函数的最值,
此时n应取最接近 的正整数值;
利用等差数列的增减性及an的符号变化
课堂小结
求等差数列前n项和Sn的最大(小)值的常用方法
(1) 通项法
利用等差数列的单调性,求出an正负转折项,或者利用性质求其正负转折项.
等差数列前n项和的应用:
大
小
