函数的综合运用课件(共54张PPT)2024年中考数学二轮复习专题
文档属性
| 名称 | 函数的综合运用课件(共54张PPT)2024年中考数学二轮复习专题 |  | |
| 格式 | pptx | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-27 22:31:19 | ||
图片预览











文档简介
(共54张PPT)
函数的综合运用
考点1.函数与面积问题
【例1】如图,直线l:y=-3x+3与x轴、y轴分别交于点A,B,抛物线y=ax2-2ax+a+4(a<0)经过点B.
(1)求该抛物线的函数表达式.
(2)已知M是抛物线上的一个动点,并且点M在第一
象限内,连接AM,BM,设点M的横坐标为m,△ABM
的面积为S,求S关于m的函数表达式,并求出S的最大值.
考点突破
分析与解答 (1)令y=-3x+3中y,x分别为0,可得
A(1,0),B(0,3).将B(0,3)代入y=ax2-2ax+a+4,可
得a=-1,即y=-x2+2x+3.(2)如图,过点M作MN∥x
轴,交AB于点N,则M(m,-m2+2m+3),N.
∴S=S△BMN+S△AMN=MN·MN·yM=MN·yB=
-(0<m<3).∴当m=时,S有最大值,最大值为 .
规律方法 (1)将图象上点的坐标代入表达式求待定系数的值,是求函数表达式的常用方法.(2)当图形面积不易求时,常过动点作x轴或y轴的垂线,分别以垂线的一部分为底或高求得面积,必要时通过割补法将图形进行转化.
1. 如图,一次函数y=ax+b(a≠0)的图象分别交x轴、
y轴于点P,Q,且与反比例函数y=(m≠0,x<0)的图
象相交于点A(-3,n)和点B(-1,-3),过点A作AC⊥
OP于点C.
(1)求反比例函数和一次函数的解析式.
将B(-1,-3)代入y=中,得=-3,解得m=3,∴反比例函数的解析式为y=(x<0).当x=-3时,n==-1,∴点A(-3,-1).将A(-3,-1),B(-1,-3)分别代入y=ax+b,得解得∴一次函数的解析式为y=-x-4.
变式练习
(2)求四边形ABOC的面积.
过点B作BD⊥x轴于点D.由(1)得AC=1,BD=3,CD=2,OD=1,∴S四边形ABOC=S梯形ABDC+S△BOD=(AC+BD)·CD+BD·OD=.
(3)直接写出当x<0时,关于x的不等式ax+b≤ 的解集.
-3≤x≤-1
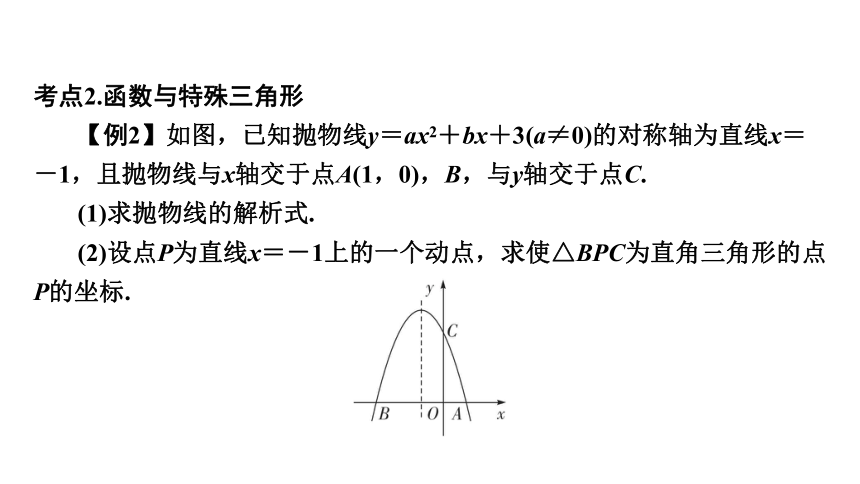
考点2.函数与特殊三角形
【例2】如图,已知抛物线y=ax2+bx+3(a≠0)的对称轴为直线x=-1,且抛物线与x轴交于点A(1,0),B,与y轴交于点C.
(1)求抛物线的解析式.
(2)设点P为直线x=-1上的一个动点,求使△BPC为直角三角形的点P的坐标.
分析与解答 (1)由抛物线的对称轴为x=-=-1,及A(1,0)可求得抛物线的解析式为y=-x2-2x+3.(2)由A(1,0)及抛物线的对称轴为直线x=-1,得B(-3,0).设点P(-1,m),则BP2=m2+4,CP2=m2-6m+10,BC2=18.当∠CBP=90°时,BP2+BC2=CP2,即m2+4+18=m2-6m+10,得m=-2;同理,当∠BCP=90°时,m=4;当∠BPC=90°时,m1=,m2=.综上所述,点P的坐标为.
规律方法 正确表示各边的长,合理运用直角三角形、等腰三角形、全等三角形的性质,结合方程思想与分类讨论思想求解即可.
2. 已知抛物线y=ax2+bx-3a经过点A(-1,0),C(0,3),与x轴交于另一点B,抛物线的顶点为D.连接BC,BD,CD.
(1)求此抛物线的解析式.
将A(-1,0),C(0,3)分别代入y=ax2+bx-3a,得解得
∴此抛物线的解析式为y=-x2+2x+3.
变式练习
(2)求证:△BCD是直角三角形.
由y=-x2+2x+3=0,得x1=-1,x2=3,
∴点B(3,0).
∵y=-x2+2x+3=-(x-1)2+4,∴点D(1,4).
∴BC2=18,CD2=2,BD2=20.∴BC2+CD2=BD2.
∴△BCD是直角三角形.
(3)在对称轴右侧的抛物线上是否存在点P,使得△PDC为等腰三角形?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.
在对称轴右侧的抛物线上存在点P,使得△PDC为等腰三角形.设点P(m,n).①当CD=DP时,由抛物线的对称性及顶点D,可得点P(2,3).②当CP=DP时,m2+(n-3)2=(m-1)2+(n-4)2,即m+n-4=0.又n=-m2+2m+3,∴m2-3m+1=0,解得m1=<1(舍去),m2=.∴n=,点P.综上所述,点P的坐标为(2,3)或.
考点3.函数与相似、全等
【例3】如图,顶点为M的抛物线y=ax2+bx(a>0)经过点A和x轴正半轴上的点B,AO=OB=2,∠AOB=120°.连接OM,AM.
(1)求抛物线的解析式.
(2)求∠AOM的大小.
(3)已知点C在x轴上,且△ABC与△AOM相似,
求点C的坐标.
分析与解答 (1)如图,过点A作AD⊥x轴于点D,由AD=AO·sin 60°=,OD=AO·cos 60°=1,得点A(-1,),将A(-1,),B(2,0)分别代入y=ax2+bx,可得y=x2-x.(2)过点M作ME⊥x轴于点E.先求得顶点M,由tan∠EOM=,得∠EOM=30°,∴∠AOM=150°.(3)连接AB,由∠ABO=30°,∠AOM=150°,可知∠ABO=∠OMA+∠OAM,∴要使△ABC与△AOM相似,点C应在点B的右边,即∠ABC=150°=∠AOM.当△ABC∽△AOM时,,可得BC=2,即点C;当△ABC∽△MOA时,,可得BC=6,即点C.综上所述,点C的坐标为.
规律方法 该类问题通常先找到一组等角,然后根据对应边成比例列方程求解;或在找到一组等角后再找另一组等角,常转化为角的存在性问题.
3. 如图,已知抛物线y=-x2+2x+3与x轴交于A,D两点,与y轴交于点B,顶点为C.连接AB,AC,BC,BD.
(1)直接写出点A,B,C,D的坐标.
点A(3,0),B(0,3),C(1,4),D(-1,0).
(2)求tan∠BAC的值.
由各点坐标,得AB=3,BC=,AC=2.∵AB2+BC2=AC2,∴△ABC是直角三角形,∠ABC=90°.∴tan∠BAC=.
变式练习
(3)在y轴上是否存在一点P,使得以P,B,D为顶点的三角形与△ABC相似?若存在,求出点P的坐标;若不存在,请说明理由.
存在.∵,∴tan∠OBD=tan∠BAC,即存在∠PBD=∠BAC.①当∠BPD=90°时,△BPD∽△ABC,此时点P在原点O处,即点P(0,0).②当∠PDB=90°时,△BDP∽△ABC,此时点P在x轴下方.∵∠ODP=90°-∠BDO=∠OBD,∴tan∠ODP=,∴OP=,点P.综上所述,点P的坐标为(0,0)或.
考点4.函数与平行四边形
【例4】如图,抛物线y=-x2-4x+c与x轴交于A,B(1,0)两点,与y轴交于点C.已知点M,N分别在抛物线及其对称轴上,是否存在点M使得以A,C,M,N为顶点的四边形是平行四边形?若存在,求出点M的坐标;若不存在,请说明理由.
分析与解答 由点B(1,0)及y=-x2-4x+c,先求得y=-x2-4x+5,再求得点A(-5,0),C(0,5),抛物线的对称轴为直线x=-2,∴点N的横坐标为-2.设点M,分以下三种情况:当AC为对角线时,-5+0=-2+m,解得m=-3,则M(-3,8);当AM为对角线时,-5+m=-2+0,解得m=3,则M(3,-16);当AN为对角线时,-5-2=0+m,解得m=-7,则M(-7,-16).综上所述,点M的坐标为(-3,8)或(3,-16)或(-7,-16).
规律方法 “两定两动”类型题目,常把抛物线上的动点作为唯一动点.以其中两个顶点作为对角线(一般分三种情况讨论),根据平行四边形的性质以及中点坐标公式转化为方程(组)求解即可,需注意四点不在同一直线上.
4. 如图,在平面直角坐标系中,直线l ∶y=kx+2与x轴、y轴分别相交于点A,B,与反比例函数y=(x>0)的图象相交于点C,已知OA=1,点C的横坐标为2.
(1)求k,m的值.
由OA=1,得点A(-1,0),代入y=kx+2,
得-k+2=0,解得k=2.∴直线l的解析式为y=2x+2.
当x=2时,y=6,∴点C(2,6).将C(2,6)代入y=,
得 =6,∴m=12.
变式练习
(2)平行于y轴的动直线与l和反比例函数的图象分别交于点D,E.若以B,D,E,O为顶点的四边形是平行四边形,求点D的坐标.
由(1)得反比例函数的解析式为y=.令y=2x+2中x=0,得y=2,∴点B(0,2).设点D(a,2a+2),则点E.∵以B,D,E,O为顶点的四边形是平行四边形,∴DE=OB=2.∴=2.①当2a+2-=2时,得2a2+2a-12=2a,解得a1=,a2=-(舍去).∴点D(,2+2).②当2a+2-=-2时,得2a2+2a-12=-2a,解得a1=-1,a2=--1(舍去).∴点D(-1,2).综上所述,点D的坐标为(,2+2)或(-1,2).
考点5.函数与角度问题
【例5】如图,抛物线y=x2-5x+4与x轴交于点A(点A在对称轴的右边),点N的坐标为(0,2),点M在抛物线上,且∠NAM=45°,求点M的坐标.
分析与解答 令x2-5x+4=0,解得x1=1,x2=4,故点A(4,0).当点M在AN的下方时,如图,将NA绕点N顺时针旋转90°到NB,连接AB与抛物线的交点即为点M.过点N作直线CD∥x轴,分别过点A,B作直线CD的垂线,垂足分别为C,D.由△ACN≌△NDB(AAS),可得点B(-2,-2),求得直线AB的解析式为y=x-,联立可得交点M.当点M在AN的上方时,同理,可得M.综上所述,点M的坐标为.
规律方法 遇角度问题时,可考虑作平行线、等腰三角形或构造含特殊角的直角三角形等.构造“一线三垂”模型,根据全等或相似的性质是求点坐标的常用方法.
5. 如图,抛物线y=-x2+bx+c与x轴交于A(-1,0),B两点,与y轴交于点C.O为坐标原点,连接AC,BC,tan∠ACO=.
(1)求抛物线的表达式.
∵OA=1,tan∠ACO=,∴OC=5,点C(0,5).将点A(-1,0),C(0,5)代入y=-x2+bx+c,得解得∴抛物线的表达式为y=-x2+4x+5.
变式练习
连接PB,过点C作CD⊥BC,交BP于点D,过点D作DE⊥y轴于点E.令-x2+4x+5=0,解得x1=-1,x2=5.∴点B(5,0),OC=OB=5.∴∠OCB=45°,BC=5.又∠BCD=90°,∴在Rt△CDE中,∠DCE=45°.∴△CDE是等腰直角三角形.∵∠ACO=∠PBC,∴tan∠ACO=tan∠PBC,即,解得CD=.∴CE=DE=1.∴点D(1,6).由B(5,0),D(1,6)可求得直线BD的表达式为y=-x+.联立解得(舍去),∴点P.
(2)P是抛物线上的一点,且在第一象限内,若∠ACO=∠PBC,求P点的坐标.
一、选择题.
1. 在平面直角坐标系中,将正比例函数y=-2x的图象向右平移3个单位长度得到一次函数y=kx+b(k≠0)的图象,则该一次函数的解析式为( ).
A.y=-2x+3 B.y=-2x+6
C.y=-2x-3 D.y=-2x-6
B
课堂练习
2. 如图,在平面直角坐标系中,点A,B在函数y=(k>0,x>0)的图象上,分别以A,B为圆心,1为半径作圆,当☉A与x轴相切、☉B与y轴相切时,连接AB.若AB=3,则k的值为( ).
A.3 B.6
C.4 D.3
第2题图
C
3. 如图,在矩形ABCD中,AB=4 cm,BC=8 cm,点P,Q同时从点B出发,终点都是点D,速度都是1 cm/s,点P的运动路径是BA→AD,点Q的运动路径是BC→CD.设线段PQ与PQ左侧矩形的边围成的阴影部分面积为S,则面积S与运动时间t之间的函数图象为( ).
第3题图
A B
C D
A
二、填空题.
4. 如图,已知一次函数y=x+1的图象与反比例函数y= 的图象在第一象限相交于点A,与x轴相交于点C,AB⊥x轴于点B.若△AOB的面积为1,则AC的长为________.(结果保留根号)
第4题图
2
5. 如图,一块矩形土地ABCD由篱笆围着,并且由一条与CD边平行的篱笆EF分开.已知篱笆的总长为900 m(篱笆的厚度忽略不计),当矩形土地ABCD的面积取得最大值时,AB=________m.
第5题图
150
6. 如图,点A,B在反比例函数y=的图象上,AC⊥y轴,垂足为D,BC⊥AC.若四边形AOBC的面积为6,,则k的值为______.
第6题图
3
7. 如图,在平面直角坐标系中,点B的坐标为(-8,6),过点B分别作x轴、y轴的垂线,垂足分别为C,A,直线y=-2x-6与AB交于点D,与y轴交于点E.动点M在线段BC上,动点N在直线y=-2x-6上.若△AMN是以点N为直角顶点的等腰直角三角形,则点M的坐标为_____________________________.
(-8,6)或
第7题图
三、解答题.
8. 如图,B是反比例函数y=(x>0)图象上一点,过点B分别向两坐标轴作垂线,垂足分别为A,C.反比例函数y=(x>0)的图象经过OB的中点M,与AB,BC分别相交于点D,E.连接DE并延长交x轴于点F,点G与点O关于点C对称,连接BF,BG.
(1)填空:k=______.
2
(2)求△BDF的面积.
连接OD.∵BA⊥y轴,∴S△BDF=S△BDO=S△BAO-
S△ADO=×8-×2=3.
第8题图
(3)求证:四边形BDFG为平行四边形.
设点D,则点B,C(4m,0),E.∵点G与点O关于点C对称,
∴点G(8m,0).∴BD=3m,CE=,BE=.
∵BD∥FG,∴△BDE∽△CFE.∴,即 .∴CF=m,点F(5m,0).∴FG=8m-5m=3m.∴BD=FG.又BD∥FG,∴四边形BDFG为平行四边形.
9. 如图,抛物线y=ax2+bx经过△OAB的三个顶点,
其中O为坐标原点,点A,点B在第一象限内,抛
物线的对称轴是直线x=,且△OAB的面积为18.
第9题图
(1)求该抛物线的函数表达式.
抛物线的对称轴为直线x=-,∴b=-a.将点A(3,-3)代入y=ax2+bx,得9a+3b=-3,联立方程组解得a=,b=-3.∴该抛物线的函数表达式为y=x2-3x.
(2)求点B的坐标.
过点A作AD⊥y轴于点D,过点B作BE⊥AD,交DA延长线于点E.设点B,则S△OAB=S四边形ODEB-S△OAD-S△ABE=(OD+BE)·DE-OD·AD-AE·BE=OD·AE+AD·BE=×3(m-3)+×3=m2-3m=18,解得m1=6,m2=-3(舍去).∴点B(6,6).
(3)设C为线段AB的中点,P为直线OB上的一个动点,连接AP,CP,将△ACP沿CP翻折,点A的对应点为A1.是否存在点P,使得以A1,P,C,B为顶点的四边形是平行四边形?若存在,求出所有符合条件的点P的坐标;若不存在,请说明理由.
存在.由点A(3,-3),B(6,6),得中点C,直线OB的解析式为y=x.∵点A,B在直线CP的两侧,点A,A1关于CP对称,∴A1P=AP,A1C=AC=BC,且点A1,B应在直线CP的同一侧,即以A1,P,C,B为顶点的四边形中,A1B不为对角线.设点P(t,t).①当BP为该平行四边形的对角线时,A1P=BC,∴AP=AC.∴AP2=AC2,即(t-3)2+(t+3)2=,解得t1=,t2=-.∴点P.
②当BC为该平行四边形的对角线时,A1C=BP,∴BP=AC.
∴BP2=AC2,即(t-6)2+(t-6)2=,解得t1=,t2=.∴点P.
∴点P.
10. 如图,抛物线y=ax2-2ax+3与x轴交于点A和点B,与y轴交于点C,连接AC,过B,C两点作直线.
(1)求a的值.
第10题图
将A(-1,0)代入y=ax2-2ax+3,得a+2a+3=0,
解得a=-1.
(2)将直线BC向下平移m(m>0)个单位长度,交抛物线于B',C'两点.在直线B'C'上方的抛物线上是否存在定点D,无论m取何值时,都是点D到直线B'C'的距离最大?若存在,请求出点D的坐标;若不存在,请说明理由.
存在.设B'C'与y轴交于点G,由(1)可得抛物线的解析式为y=-x2+2x+3,当y=-x2+2x+3=0时,解得x1=-1,x2=3;当x=0时,y=3.∴点A(-1,0),B(3,0),C(0,3).∴OB=OC.又∠BOC=90°.∴△BOC是等腰直角三角形,∠BCO=45°.∵B'C'∥BC,∴∠B'GO=∠BCO=45°.
设点D(t,-t2+2t+3),过点D作DE∥y轴,交B'C'于点E,作DF⊥B'C'于点F.∴∠DEF=∠B'GO=45°,△DEF是等腰直角三角形.由B(3,0),C(0,3),可得直线BC的解析式为 y=-x+3.将直线BC向下平移m(m>0)个单位长度,得直线B'C'的解析式为y=-x+3-m,∴点E(t,-t+3-m),DE=-t2+2t+3-(-t+3-m)=-+m.当t=时,DE有最大值+m,此时DF=DE也有最大值,
∴点D.
(3)抛物线上是否存在点P,使∠PBC+∠ACO=45°?若存在,请求出直线BP的解析式;若不存在,请说明理由.
存在.①当点P在直线BC下方时,在y轴上取点H(0,1),作直线BH交抛物线于点P(异于点B).由(2)知∠OBC=45°.∵tan∠ACO=,tan∠HBO=,∴∠ACO=∠HBO.∴∠PBC+∠ACO=∠PBC+∠HBO=45°.由B(3,0),H(0,1),可得直线BP的解析式为y=-x+1.
②当点P在直线BC上方时,在x轴上取点I(1,0),连接CI,过点B作直线BP∥CI交抛物线于点P(异于点B).∴∠PBC=∠BCI.∵tan∠ICO==tan∠ACO,∴∠ACO=∠ICO.∴∠PBC+∠ACO=∠BCI+∠ICO=∠BCO=45°.由I(1,0),C(0,3),可得直线CI的解析式为y=-3x+3.由BP∥CI可设直线BP的解析式为y=-3x+k,将点B(3,0)代入,得y=-3x+9.综上所述,直线BP的解析式为y=-x+1或y=-3x+9.
11. 如图,抛物线y=ax2+bx+2与x轴交于点A和点B,与y轴交于点C,连接BC,点P(m>0)为抛物线上一动点,过点P作PN⊥x轴交直线BC于点M,交x轴于点N.
(1)直接写出抛物线和直线BC的解析式.
第11题图
抛物线的解析式为y=-x2+x+2,直线BC的解析式为
y=-x+2.
(2)连接OM,当△OCM为等腰三角形时,求m的值.
由题意得点C(0,2),M(m,-m+2),m>0.∴OC2=4,CM2=2m2,OM2=2m2-4m+4.当△OCM为等腰三角形时,分以下三种情况讨论.①当CM=OM时,CM2=OM2,即2m2=2m2-4m+4,解得m=1.②当CM=OC时,CM2=OC2,即2m2=4,解得m1=,m2=-(舍去).③当OM=OC时,OM2=OC2,即2m2-4m+4=4,解得m1=2,m2=0(舍去).综上所述,m=1或 或2.
(3)当点P在运动过程中,在y轴上是否存在点Q,使得以O,P,Q为顶点的三角形与以B,C,N为顶点的三角形相似(其中点P与点C相对应)?若存在,直接写出点P和点Q的坐标;若不存在,请说明理由.
P(),Q(0,-1);或P,Q;或P(1+,-1-),Q(0,1);或P(1+,-3-),Q(0,-2).提示:△POQ∽△CBN或△POQ∽△CNB,可按点P在点B左侧或右侧进行分类讨论.
1. (2022·广东)如图,抛物线y=x2+bx+c的顶点为C,与x轴交于A(1,0),B两点,AB=4,P是线段AB上的动点,过点P作PQ∥BC,交AC于点Q.
(1)求该抛物线的解析式.
第1题图
由题意知点B(-3,0),∴解得
∴该抛物线的解析式为y=x2+2x-3.
强化练习
(2)求△CPQ面积的最大值,并求此时点P坐标.
过点Q作QE⊥x轴于点E,过点C作CF⊥x轴于点F.设点P(m,0),则PA=1-m.∵y=x2+2x-3=(x+1)2-4,∴点C(-1,-4).∴CF=4.
∵PQ∥BC,∴△PQA∽△BCA.∴,即 .
∴QE=1-m.∴S△CPQ=S△PCA-S△PQA=PA·CF-PA·QE=-(m+1)2+2.∵-3≤m≤1,∴当m=-1时,S△CPQ有最大值2.∴△CPQ面积的最大值为2,此时点P的坐标为(-1,0).
2. (2023·眉山)如图,在平面直角坐标系中,直线y=kx+b与x轴交于点A(4,0),与y轴交于点B(0,2),与反比例函数y= 在第四象限内的图象交于点C(6,a).
(1)求反比例函数的表达式.
第2题图
将点A(4,0),B(0,2)代入y=kx+b,得
解得∴一次函数的表达式为y=-x+2.
当x=6时,y=-1,∴点C(6,-1).将点C(6,-1)代入y=,得m=-6,∴反比例函数的表达式为y=-.
(2)当kx+b> 时,直接写出x的取值范围.
x<-2或0<x<6.
(3)在双曲线y=上是否存在点P,使△ABP是以A为直角顶点的直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.
存在.过点A作AE⊥BC,交y轴于点E.∵∠BAO+∠EAO=90°,∠AEO+∠EAO=90°,∴∠BAO=∠AEO.又∠AOB=∠EOA=90°,∴△AOB∽△EOA.
∴,即.∴EO=8,点E(0,-8).由A(4,0),E(0,-8)可得直线AE的表达式为y=2x-8.联立解得∴点P的坐标为(1,-6)或(3,-2)
3. (2023·自贡)如图,抛物线y=-x2+bx+4与x轴交于A,B两点,与y轴交于点C.
(1)求抛物线的解析式及B,C两点的坐标.
第3题图
将点A(-3,0)代入y=-x2+bx+4,得-×9-3b+4
=0,解得b=-.∴抛物线的解析式为y=-x2-x+4.
当y=0时,-x2-x+4=0,解得x1=1,x2=-3;当x=0时,y=4.
∴点B(1,0),C(0,4).
(2)若以A,B,C,D为顶点的四边形是平行四边形,求点D的坐标.
设点D(m,n),分以下三种情况.
①当AB为对角线时,-3+1=0+m,0+0=4+n,解得m=-2,n=-4,则点D(-2,-4).
②当AC为对角线时,-3+0=1+m,0+4=0+n,解得m=-4,n=4,则点D(-4,4).
③当AD为对角线时,-3+m=0+1,0+n=0+4,解得m=4,n=4,则点D(4,4).综上所述,点D的坐标为(-2,-4)或(-4,4)或(4,4).
(3)该抛物线的对称轴上是否存在点E,使得∠ACE=45°?若存在,求出点E的坐标;若不存在,请说明理由.
存在.易知点E在直线AC上方.过点A作AF⊥CE,交CE的延长线于点F,过点F作FM⊥x轴于点M,FN⊥y轴于点N,则四边形OMFN是矩形,∠MFN=∠AMF=∠CNF=90°,OM=FN,ON=FM.∵∠ACF=45°,∠AFC=90°,∴△ACF是等腰直角三角形,AF=CF.∴∠MFA=90°-∠AFN=∠NFC.∴△AFM≌△CFN.∴FM=FN,AM=CN.∴OM=ON.∴OA+AM=OC-CN,即3+AM=4-AM.∴AM=CN=,点 F.由C(0,4),F可求得直线CF的解析式为y=x+4.当x=-1时,y=x+4=,∴点E.
4. (2023·朝阳)如图,抛物线y=-x2+bx+c与x轴分别交于点A(-2,0),B(4,0),与y轴交于点C,连接BC.
(1)求抛物线的解析式.
第4题图
将A(-2,0),B(4,0)代入y=-x2+bx+c,
得解得
∴抛物线的解析式为y=-x2+x+4.
(2)P是第一象限内抛物线上的一个动点,过点P作直线l⊥x轴于点M(m,0),交BC于点N,连接CM,PB,PC.△PCB的面积记为S1,△BCM的面积记为S2,当S1=S2时,求m的值.
令x=0,则y=-x2+x+4=4.∴点C(0,4).由B(4,0),C(0,4)可求得直线BC的解析式为y=-x+4.由M(m,0),得P,N(m,-m+4).∴PN=-m2+2m,S1=PN·OB=-m2+4m,S2=BM·OC=8-2m.由S1=S2,得 -m2+4m=8-2m,解得m1=2,m2=4(舍去).∴当S1=S2时,m=2.
(3)在(2)的条件下,点Q在抛物线上,直线MQ与直线BC交于点H,当△HMN与△BCM相似时,请直接写出点Q的坐标.
Q或(-2+2,-12+6)或(-2-2,-12-6).提示:由B(4,0),C(0,4),可知△BOC是等腰直角三角形,∠CBO=45°,∴△BMN是等腰直角三角形,∠BNM=∠MBN=45°.∵△HMN与△BCM相似,且∠MNH=∠CBM=45°,∴点H在MN的右侧,且 或 .设点H(t,-t+4).由(2)知点M(2,0),N(2,2),B(4,0),C(0,4),∴BC=4,MB=2,MN=2,NH=(t-2).
当 时,,解得t=6.∴点H(6,-2),可求得直线MH的解析式为y=-x+1.联立解得∴点Q或.当 时,同理,得点 H,求得点Q(-2+2,-12+6)或(-2-2,-12-6).
函数的综合运用
考点1.函数与面积问题
【例1】如图,直线l:y=-3x+3与x轴、y轴分别交于点A,B,抛物线y=ax2-2ax+a+4(a<0)经过点B.
(1)求该抛物线的函数表达式.
(2)已知M是抛物线上的一个动点,并且点M在第一
象限内,连接AM,BM,设点M的横坐标为m,△ABM
的面积为S,求S关于m的函数表达式,并求出S的最大值.
考点突破
分析与解答 (1)令y=-3x+3中y,x分别为0,可得
A(1,0),B(0,3).将B(0,3)代入y=ax2-2ax+a+4,可
得a=-1,即y=-x2+2x+3.(2)如图,过点M作MN∥x
轴,交AB于点N,则M(m,-m2+2m+3),N.
∴S=S△BMN+S△AMN=MN·MN·yM=MN·yB=
-(0<m<3).∴当m=时,S有最大值,最大值为 .
规律方法 (1)将图象上点的坐标代入表达式求待定系数的值,是求函数表达式的常用方法.(2)当图形面积不易求时,常过动点作x轴或y轴的垂线,分别以垂线的一部分为底或高求得面积,必要时通过割补法将图形进行转化.
1. 如图,一次函数y=ax+b(a≠0)的图象分别交x轴、
y轴于点P,Q,且与反比例函数y=(m≠0,x<0)的图
象相交于点A(-3,n)和点B(-1,-3),过点A作AC⊥
OP于点C.
(1)求反比例函数和一次函数的解析式.
将B(-1,-3)代入y=中,得=-3,解得m=3,∴反比例函数的解析式为y=(x<0).当x=-3时,n==-1,∴点A(-3,-1).将A(-3,-1),B(-1,-3)分别代入y=ax+b,得解得∴一次函数的解析式为y=-x-4.
变式练习
(2)求四边形ABOC的面积.
过点B作BD⊥x轴于点D.由(1)得AC=1,BD=3,CD=2,OD=1,∴S四边形ABOC=S梯形ABDC+S△BOD=(AC+BD)·CD+BD·OD=.
(3)直接写出当x<0时,关于x的不等式ax+b≤ 的解集.
-3≤x≤-1
考点2.函数与特殊三角形
【例2】如图,已知抛物线y=ax2+bx+3(a≠0)的对称轴为直线x=-1,且抛物线与x轴交于点A(1,0),B,与y轴交于点C.
(1)求抛物线的解析式.
(2)设点P为直线x=-1上的一个动点,求使△BPC为直角三角形的点P的坐标.
分析与解答 (1)由抛物线的对称轴为x=-=-1,及A(1,0)可求得抛物线的解析式为y=-x2-2x+3.(2)由A(1,0)及抛物线的对称轴为直线x=-1,得B(-3,0).设点P(-1,m),则BP2=m2+4,CP2=m2-6m+10,BC2=18.当∠CBP=90°时,BP2+BC2=CP2,即m2+4+18=m2-6m+10,得m=-2;同理,当∠BCP=90°时,m=4;当∠BPC=90°时,m1=,m2=.综上所述,点P的坐标为.
规律方法 正确表示各边的长,合理运用直角三角形、等腰三角形、全等三角形的性质,结合方程思想与分类讨论思想求解即可.
2. 已知抛物线y=ax2+bx-3a经过点A(-1,0),C(0,3),与x轴交于另一点B,抛物线的顶点为D.连接BC,BD,CD.
(1)求此抛物线的解析式.
将A(-1,0),C(0,3)分别代入y=ax2+bx-3a,得解得
∴此抛物线的解析式为y=-x2+2x+3.
变式练习
(2)求证:△BCD是直角三角形.
由y=-x2+2x+3=0,得x1=-1,x2=3,
∴点B(3,0).
∵y=-x2+2x+3=-(x-1)2+4,∴点D(1,4).
∴BC2=18,CD2=2,BD2=20.∴BC2+CD2=BD2.
∴△BCD是直角三角形.
(3)在对称轴右侧的抛物线上是否存在点P,使得△PDC为等腰三角形?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.
在对称轴右侧的抛物线上存在点P,使得△PDC为等腰三角形.设点P(m,n).①当CD=DP时,由抛物线的对称性及顶点D,可得点P(2,3).②当CP=DP时,m2+(n-3)2=(m-1)2+(n-4)2,即m+n-4=0.又n=-m2+2m+3,∴m2-3m+1=0,解得m1=<1(舍去),m2=.∴n=,点P.综上所述,点P的坐标为(2,3)或.
考点3.函数与相似、全等
【例3】如图,顶点为M的抛物线y=ax2+bx(a>0)经过点A和x轴正半轴上的点B,AO=OB=2,∠AOB=120°.连接OM,AM.
(1)求抛物线的解析式.
(2)求∠AOM的大小.
(3)已知点C在x轴上,且△ABC与△AOM相似,
求点C的坐标.
分析与解答 (1)如图,过点A作AD⊥x轴于点D,由AD=AO·sin 60°=,OD=AO·cos 60°=1,得点A(-1,),将A(-1,),B(2,0)分别代入y=ax2+bx,可得y=x2-x.(2)过点M作ME⊥x轴于点E.先求得顶点M,由tan∠EOM=,得∠EOM=30°,∴∠AOM=150°.(3)连接AB,由∠ABO=30°,∠AOM=150°,可知∠ABO=∠OMA+∠OAM,∴要使△ABC与△AOM相似,点C应在点B的右边,即∠ABC=150°=∠AOM.当△ABC∽△AOM时,,可得BC=2,即点C;当△ABC∽△MOA时,,可得BC=6,即点C.综上所述,点C的坐标为.
规律方法 该类问题通常先找到一组等角,然后根据对应边成比例列方程求解;或在找到一组等角后再找另一组等角,常转化为角的存在性问题.
3. 如图,已知抛物线y=-x2+2x+3与x轴交于A,D两点,与y轴交于点B,顶点为C.连接AB,AC,BC,BD.
(1)直接写出点A,B,C,D的坐标.
点A(3,0),B(0,3),C(1,4),D(-1,0).
(2)求tan∠BAC的值.
由各点坐标,得AB=3,BC=,AC=2.∵AB2+BC2=AC2,∴△ABC是直角三角形,∠ABC=90°.∴tan∠BAC=.
变式练习
(3)在y轴上是否存在一点P,使得以P,B,D为顶点的三角形与△ABC相似?若存在,求出点P的坐标;若不存在,请说明理由.
存在.∵,∴tan∠OBD=tan∠BAC,即存在∠PBD=∠BAC.①当∠BPD=90°时,△BPD∽△ABC,此时点P在原点O处,即点P(0,0).②当∠PDB=90°时,△BDP∽△ABC,此时点P在x轴下方.∵∠ODP=90°-∠BDO=∠OBD,∴tan∠ODP=,∴OP=,点P.综上所述,点P的坐标为(0,0)或.
考点4.函数与平行四边形
【例4】如图,抛物线y=-x2-4x+c与x轴交于A,B(1,0)两点,与y轴交于点C.已知点M,N分别在抛物线及其对称轴上,是否存在点M使得以A,C,M,N为顶点的四边形是平行四边形?若存在,求出点M的坐标;若不存在,请说明理由.
分析与解答 由点B(1,0)及y=-x2-4x+c,先求得y=-x2-4x+5,再求得点A(-5,0),C(0,5),抛物线的对称轴为直线x=-2,∴点N的横坐标为-2.设点M,分以下三种情况:当AC为对角线时,-5+0=-2+m,解得m=-3,则M(-3,8);当AM为对角线时,-5+m=-2+0,解得m=3,则M(3,-16);当AN为对角线时,-5-2=0+m,解得m=-7,则M(-7,-16).综上所述,点M的坐标为(-3,8)或(3,-16)或(-7,-16).
规律方法 “两定两动”类型题目,常把抛物线上的动点作为唯一动点.以其中两个顶点作为对角线(一般分三种情况讨论),根据平行四边形的性质以及中点坐标公式转化为方程(组)求解即可,需注意四点不在同一直线上.
4. 如图,在平面直角坐标系中,直线l ∶y=kx+2与x轴、y轴分别相交于点A,B,与反比例函数y=(x>0)的图象相交于点C,已知OA=1,点C的横坐标为2.
(1)求k,m的值.
由OA=1,得点A(-1,0),代入y=kx+2,
得-k+2=0,解得k=2.∴直线l的解析式为y=2x+2.
当x=2时,y=6,∴点C(2,6).将C(2,6)代入y=,
得 =6,∴m=12.
变式练习
(2)平行于y轴的动直线与l和反比例函数的图象分别交于点D,E.若以B,D,E,O为顶点的四边形是平行四边形,求点D的坐标.
由(1)得反比例函数的解析式为y=.令y=2x+2中x=0,得y=2,∴点B(0,2).设点D(a,2a+2),则点E.∵以B,D,E,O为顶点的四边形是平行四边形,∴DE=OB=2.∴=2.①当2a+2-=2时,得2a2+2a-12=2a,解得a1=,a2=-(舍去).∴点D(,2+2).②当2a+2-=-2时,得2a2+2a-12=-2a,解得a1=-1,a2=--1(舍去).∴点D(-1,2).综上所述,点D的坐标为(,2+2)或(-1,2).
考点5.函数与角度问题
【例5】如图,抛物线y=x2-5x+4与x轴交于点A(点A在对称轴的右边),点N的坐标为(0,2),点M在抛物线上,且∠NAM=45°,求点M的坐标.
分析与解答 令x2-5x+4=0,解得x1=1,x2=4,故点A(4,0).当点M在AN的下方时,如图,将NA绕点N顺时针旋转90°到NB,连接AB与抛物线的交点即为点M.过点N作直线CD∥x轴,分别过点A,B作直线CD的垂线,垂足分别为C,D.由△ACN≌△NDB(AAS),可得点B(-2,-2),求得直线AB的解析式为y=x-,联立可得交点M.当点M在AN的上方时,同理,可得M.综上所述,点M的坐标为.
规律方法 遇角度问题时,可考虑作平行线、等腰三角形或构造含特殊角的直角三角形等.构造“一线三垂”模型,根据全等或相似的性质是求点坐标的常用方法.
5. 如图,抛物线y=-x2+bx+c与x轴交于A(-1,0),B两点,与y轴交于点C.O为坐标原点,连接AC,BC,tan∠ACO=.
(1)求抛物线的表达式.
∵OA=1,tan∠ACO=,∴OC=5,点C(0,5).将点A(-1,0),C(0,5)代入y=-x2+bx+c,得解得∴抛物线的表达式为y=-x2+4x+5.
变式练习
连接PB,过点C作CD⊥BC,交BP于点D,过点D作DE⊥y轴于点E.令-x2+4x+5=0,解得x1=-1,x2=5.∴点B(5,0),OC=OB=5.∴∠OCB=45°,BC=5.又∠BCD=90°,∴在Rt△CDE中,∠DCE=45°.∴△CDE是等腰直角三角形.∵∠ACO=∠PBC,∴tan∠ACO=tan∠PBC,即,解得CD=.∴CE=DE=1.∴点D(1,6).由B(5,0),D(1,6)可求得直线BD的表达式为y=-x+.联立解得(舍去),∴点P.
(2)P是抛物线上的一点,且在第一象限内,若∠ACO=∠PBC,求P点的坐标.
一、选择题.
1. 在平面直角坐标系中,将正比例函数y=-2x的图象向右平移3个单位长度得到一次函数y=kx+b(k≠0)的图象,则该一次函数的解析式为( ).
A.y=-2x+3 B.y=-2x+6
C.y=-2x-3 D.y=-2x-6
B
课堂练习
2. 如图,在平面直角坐标系中,点A,B在函数y=(k>0,x>0)的图象上,分别以A,B为圆心,1为半径作圆,当☉A与x轴相切、☉B与y轴相切时,连接AB.若AB=3,则k的值为( ).
A.3 B.6
C.4 D.3
第2题图
C
3. 如图,在矩形ABCD中,AB=4 cm,BC=8 cm,点P,Q同时从点B出发,终点都是点D,速度都是1 cm/s,点P的运动路径是BA→AD,点Q的运动路径是BC→CD.设线段PQ与PQ左侧矩形的边围成的阴影部分面积为S,则面积S与运动时间t之间的函数图象为( ).
第3题图
A B
C D
A
二、填空题.
4. 如图,已知一次函数y=x+1的图象与反比例函数y= 的图象在第一象限相交于点A,与x轴相交于点C,AB⊥x轴于点B.若△AOB的面积为1,则AC的长为________.(结果保留根号)
第4题图
2
5. 如图,一块矩形土地ABCD由篱笆围着,并且由一条与CD边平行的篱笆EF分开.已知篱笆的总长为900 m(篱笆的厚度忽略不计),当矩形土地ABCD的面积取得最大值时,AB=________m.
第5题图
150
6. 如图,点A,B在反比例函数y=的图象上,AC⊥y轴,垂足为D,BC⊥AC.若四边形AOBC的面积为6,,则k的值为______.
第6题图
3
7. 如图,在平面直角坐标系中,点B的坐标为(-8,6),过点B分别作x轴、y轴的垂线,垂足分别为C,A,直线y=-2x-6与AB交于点D,与y轴交于点E.动点M在线段BC上,动点N在直线y=-2x-6上.若△AMN是以点N为直角顶点的等腰直角三角形,则点M的坐标为_____________________________.
(-8,6)或
第7题图
三、解答题.
8. 如图,B是反比例函数y=(x>0)图象上一点,过点B分别向两坐标轴作垂线,垂足分别为A,C.反比例函数y=(x>0)的图象经过OB的中点M,与AB,BC分别相交于点D,E.连接DE并延长交x轴于点F,点G与点O关于点C对称,连接BF,BG.
(1)填空:k=______.
2
(2)求△BDF的面积.
连接OD.∵BA⊥y轴,∴S△BDF=S△BDO=S△BAO-
S△ADO=×8-×2=3.
第8题图
(3)求证:四边形BDFG为平行四边形.
设点D,则点B,C(4m,0),E.∵点G与点O关于点C对称,
∴点G(8m,0).∴BD=3m,CE=,BE=.
∵BD∥FG,∴△BDE∽△CFE.∴,即 .∴CF=m,点F(5m,0).∴FG=8m-5m=3m.∴BD=FG.又BD∥FG,∴四边形BDFG为平行四边形.
9. 如图,抛物线y=ax2+bx经过△OAB的三个顶点,
其中O为坐标原点,点A,点B在第一象限内,抛
物线的对称轴是直线x=,且△OAB的面积为18.
第9题图
(1)求该抛物线的函数表达式.
抛物线的对称轴为直线x=-,∴b=-a.将点A(3,-3)代入y=ax2+bx,得9a+3b=-3,联立方程组解得a=,b=-3.∴该抛物线的函数表达式为y=x2-3x.
(2)求点B的坐标.
过点A作AD⊥y轴于点D,过点B作BE⊥AD,交DA延长线于点E.设点B,则S△OAB=S四边形ODEB-S△OAD-S△ABE=(OD+BE)·DE-OD·AD-AE·BE=OD·AE+AD·BE=×3(m-3)+×3=m2-3m=18,解得m1=6,m2=-3(舍去).∴点B(6,6).
(3)设C为线段AB的中点,P为直线OB上的一个动点,连接AP,CP,将△ACP沿CP翻折,点A的对应点为A1.是否存在点P,使得以A1,P,C,B为顶点的四边形是平行四边形?若存在,求出所有符合条件的点P的坐标;若不存在,请说明理由.
存在.由点A(3,-3),B(6,6),得中点C,直线OB的解析式为y=x.∵点A,B在直线CP的两侧,点A,A1关于CP对称,∴A1P=AP,A1C=AC=BC,且点A1,B应在直线CP的同一侧,即以A1,P,C,B为顶点的四边形中,A1B不为对角线.设点P(t,t).①当BP为该平行四边形的对角线时,A1P=BC,∴AP=AC.∴AP2=AC2,即(t-3)2+(t+3)2=,解得t1=,t2=-.∴点P.
②当BC为该平行四边形的对角线时,A1C=BP,∴BP=AC.
∴BP2=AC2,即(t-6)2+(t-6)2=,解得t1=,t2=.∴点P.
∴点P.
10. 如图,抛物线y=ax2-2ax+3与x轴交于点A和点B,与y轴交于点C,连接AC,过B,C两点作直线.
(1)求a的值.
第10题图
将A(-1,0)代入y=ax2-2ax+3,得a+2a+3=0,
解得a=-1.
(2)将直线BC向下平移m(m>0)个单位长度,交抛物线于B',C'两点.在直线B'C'上方的抛物线上是否存在定点D,无论m取何值时,都是点D到直线B'C'的距离最大?若存在,请求出点D的坐标;若不存在,请说明理由.
存在.设B'C'与y轴交于点G,由(1)可得抛物线的解析式为y=-x2+2x+3,当y=-x2+2x+3=0时,解得x1=-1,x2=3;当x=0时,y=3.∴点A(-1,0),B(3,0),C(0,3).∴OB=OC.又∠BOC=90°.∴△BOC是等腰直角三角形,∠BCO=45°.∵B'C'∥BC,∴∠B'GO=∠BCO=45°.
设点D(t,-t2+2t+3),过点D作DE∥y轴,交B'C'于点E,作DF⊥B'C'于点F.∴∠DEF=∠B'GO=45°,△DEF是等腰直角三角形.由B(3,0),C(0,3),可得直线BC的解析式为 y=-x+3.将直线BC向下平移m(m>0)个单位长度,得直线B'C'的解析式为y=-x+3-m,∴点E(t,-t+3-m),DE=-t2+2t+3-(-t+3-m)=-+m.当t=时,DE有最大值+m,此时DF=DE也有最大值,
∴点D.
(3)抛物线上是否存在点P,使∠PBC+∠ACO=45°?若存在,请求出直线BP的解析式;若不存在,请说明理由.
存在.①当点P在直线BC下方时,在y轴上取点H(0,1),作直线BH交抛物线于点P(异于点B).由(2)知∠OBC=45°.∵tan∠ACO=,tan∠HBO=,∴∠ACO=∠HBO.∴∠PBC+∠ACO=∠PBC+∠HBO=45°.由B(3,0),H(0,1),可得直线BP的解析式为y=-x+1.
②当点P在直线BC上方时,在x轴上取点I(1,0),连接CI,过点B作直线BP∥CI交抛物线于点P(异于点B).∴∠PBC=∠BCI.∵tan∠ICO==tan∠ACO,∴∠ACO=∠ICO.∴∠PBC+∠ACO=∠BCI+∠ICO=∠BCO=45°.由I(1,0),C(0,3),可得直线CI的解析式为y=-3x+3.由BP∥CI可设直线BP的解析式为y=-3x+k,将点B(3,0)代入,得y=-3x+9.综上所述,直线BP的解析式为y=-x+1或y=-3x+9.
11. 如图,抛物线y=ax2+bx+2与x轴交于点A和点B,与y轴交于点C,连接BC,点P(m>0)为抛物线上一动点,过点P作PN⊥x轴交直线BC于点M,交x轴于点N.
(1)直接写出抛物线和直线BC的解析式.
第11题图
抛物线的解析式为y=-x2+x+2,直线BC的解析式为
y=-x+2.
(2)连接OM,当△OCM为等腰三角形时,求m的值.
由题意得点C(0,2),M(m,-m+2),m>0.∴OC2=4,CM2=2m2,OM2=2m2-4m+4.当△OCM为等腰三角形时,分以下三种情况讨论.①当CM=OM时,CM2=OM2,即2m2=2m2-4m+4,解得m=1.②当CM=OC时,CM2=OC2,即2m2=4,解得m1=,m2=-(舍去).③当OM=OC时,OM2=OC2,即2m2-4m+4=4,解得m1=2,m2=0(舍去).综上所述,m=1或 或2.
(3)当点P在运动过程中,在y轴上是否存在点Q,使得以O,P,Q为顶点的三角形与以B,C,N为顶点的三角形相似(其中点P与点C相对应)?若存在,直接写出点P和点Q的坐标;若不存在,请说明理由.
P(),Q(0,-1);或P,Q;或P(1+,-1-),Q(0,1);或P(1+,-3-),Q(0,-2).提示:△POQ∽△CBN或△POQ∽△CNB,可按点P在点B左侧或右侧进行分类讨论.
1. (2022·广东)如图,抛物线y=x2+bx+c的顶点为C,与x轴交于A(1,0),B两点,AB=4,P是线段AB上的动点,过点P作PQ∥BC,交AC于点Q.
(1)求该抛物线的解析式.
第1题图
由题意知点B(-3,0),∴解得
∴该抛物线的解析式为y=x2+2x-3.
强化练习
(2)求△CPQ面积的最大值,并求此时点P坐标.
过点Q作QE⊥x轴于点E,过点C作CF⊥x轴于点F.设点P(m,0),则PA=1-m.∵y=x2+2x-3=(x+1)2-4,∴点C(-1,-4).∴CF=4.
∵PQ∥BC,∴△PQA∽△BCA.∴,即 .
∴QE=1-m.∴S△CPQ=S△PCA-S△PQA=PA·CF-PA·QE=-(m+1)2+2.∵-3≤m≤1,∴当m=-1时,S△CPQ有最大值2.∴△CPQ面积的最大值为2,此时点P的坐标为(-1,0).
2. (2023·眉山)如图,在平面直角坐标系中,直线y=kx+b与x轴交于点A(4,0),与y轴交于点B(0,2),与反比例函数y= 在第四象限内的图象交于点C(6,a).
(1)求反比例函数的表达式.
第2题图
将点A(4,0),B(0,2)代入y=kx+b,得
解得∴一次函数的表达式为y=-x+2.
当x=6时,y=-1,∴点C(6,-1).将点C(6,-1)代入y=,得m=-6,∴反比例函数的表达式为y=-.
(2)当kx+b> 时,直接写出x的取值范围.
x<-2或0<x<6.
(3)在双曲线y=上是否存在点P,使△ABP是以A为直角顶点的直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.
存在.过点A作AE⊥BC,交y轴于点E.∵∠BAO+∠EAO=90°,∠AEO+∠EAO=90°,∴∠BAO=∠AEO.又∠AOB=∠EOA=90°,∴△AOB∽△EOA.
∴,即.∴EO=8,点E(0,-8).由A(4,0),E(0,-8)可得直线AE的表达式为y=2x-8.联立解得∴点P的坐标为(1,-6)或(3,-2)
3. (2023·自贡)如图,抛物线y=-x2+bx+4与x轴交于A,B两点,与y轴交于点C.
(1)求抛物线的解析式及B,C两点的坐标.
第3题图
将点A(-3,0)代入y=-x2+bx+4,得-×9-3b+4
=0,解得b=-.∴抛物线的解析式为y=-x2-x+4.
当y=0时,-x2-x+4=0,解得x1=1,x2=-3;当x=0时,y=4.
∴点B(1,0),C(0,4).
(2)若以A,B,C,D为顶点的四边形是平行四边形,求点D的坐标.
设点D(m,n),分以下三种情况.
①当AB为对角线时,-3+1=0+m,0+0=4+n,解得m=-2,n=-4,则点D(-2,-4).
②当AC为对角线时,-3+0=1+m,0+4=0+n,解得m=-4,n=4,则点D(-4,4).
③当AD为对角线时,-3+m=0+1,0+n=0+4,解得m=4,n=4,则点D(4,4).综上所述,点D的坐标为(-2,-4)或(-4,4)或(4,4).
(3)该抛物线的对称轴上是否存在点E,使得∠ACE=45°?若存在,求出点E的坐标;若不存在,请说明理由.
存在.易知点E在直线AC上方.过点A作AF⊥CE,交CE的延长线于点F,过点F作FM⊥x轴于点M,FN⊥y轴于点N,则四边形OMFN是矩形,∠MFN=∠AMF=∠CNF=90°,OM=FN,ON=FM.∵∠ACF=45°,∠AFC=90°,∴△ACF是等腰直角三角形,AF=CF.∴∠MFA=90°-∠AFN=∠NFC.∴△AFM≌△CFN.∴FM=FN,AM=CN.∴OM=ON.∴OA+AM=OC-CN,即3+AM=4-AM.∴AM=CN=,点 F.由C(0,4),F可求得直线CF的解析式为y=x+4.当x=-1时,y=x+4=,∴点E.
4. (2023·朝阳)如图,抛物线y=-x2+bx+c与x轴分别交于点A(-2,0),B(4,0),与y轴交于点C,连接BC.
(1)求抛物线的解析式.
第4题图
将A(-2,0),B(4,0)代入y=-x2+bx+c,
得解得
∴抛物线的解析式为y=-x2+x+4.
(2)P是第一象限内抛物线上的一个动点,过点P作直线l⊥x轴于点M(m,0),交BC于点N,连接CM,PB,PC.△PCB的面积记为S1,△BCM的面积记为S2,当S1=S2时,求m的值.
令x=0,则y=-x2+x+4=4.∴点C(0,4).由B(4,0),C(0,4)可求得直线BC的解析式为y=-x+4.由M(m,0),得P,N(m,-m+4).∴PN=-m2+2m,S1=PN·OB=-m2+4m,S2=BM·OC=8-2m.由S1=S2,得 -m2+4m=8-2m,解得m1=2,m2=4(舍去).∴当S1=S2时,m=2.
(3)在(2)的条件下,点Q在抛物线上,直线MQ与直线BC交于点H,当△HMN与△BCM相似时,请直接写出点Q的坐标.
Q或(-2+2,-12+6)或(-2-2,-12-6).提示:由B(4,0),C(0,4),可知△BOC是等腰直角三角形,∠CBO=45°,∴△BMN是等腰直角三角形,∠BNM=∠MBN=45°.∵△HMN与△BCM相似,且∠MNH=∠CBM=45°,∴点H在MN的右侧,且 或 .设点H(t,-t+4).由(2)知点M(2,0),N(2,2),B(4,0),C(0,4),∴BC=4,MB=2,MN=2,NH=(t-2).
当 时,,解得t=6.∴点H(6,-2),可求得直线MH的解析式为y=-x+1.联立解得∴点Q或.当 时,同理,得点 H,求得点Q(-2+2,-12+6)或(-2-2,-12-6).
同课章节目录
