数学人教A版(2019)必修第一册5.1.2弧度制(共21张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第一册5.1.2弧度制(共21张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-27 21:21:54 | ||
图片预览





文档简介
(共21张PPT)
5.1.2 弧度制
第五章 三角函数
姚明身高
姚明,
身高 7尺6寸,体重310磅;
英文名:Yao Ming
身高:226厘米
体重:134公斤
出生地点:上海
引 入
这种用度做单位来度量角的单位制叫做角度制.
1°=60′,1′=60″.
那些年 我们学习过了角度制,
在角度制中,1°角的规定_______________________________.
[答案] 将圆周分成360等份,一份弧所对的圆心角规定为1度角.
不同的单位制能给解决问题带来方便.
角的度量是否也能用不同的单位制呢?
能否像度量长度那样,用十进制的实数来度量角的大小呢?
思考: 能否计算?
探究新知
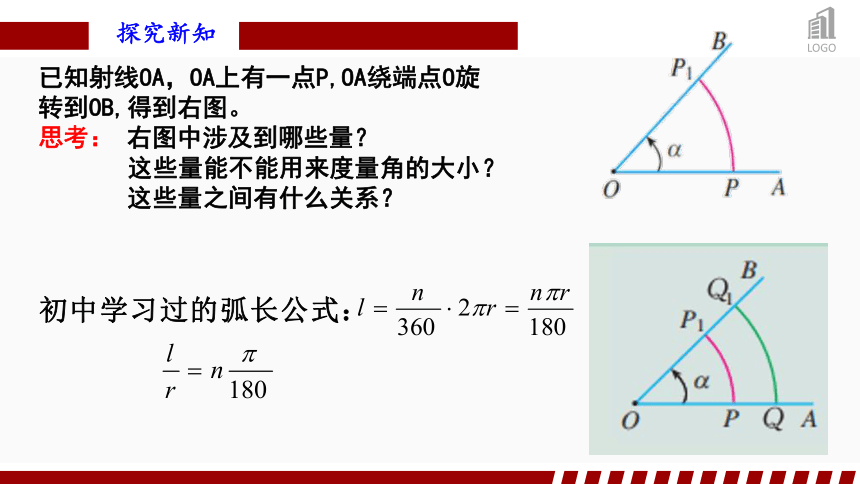
初中学习过的弧长公式:
已知射线OA,OA上有一点P,OA绕端点O旋转到OB,得到右图。
思考: 右图中涉及到哪些量?
这些量能不能用来度量角的大小?
这些量之间有什么关系?
探究新知
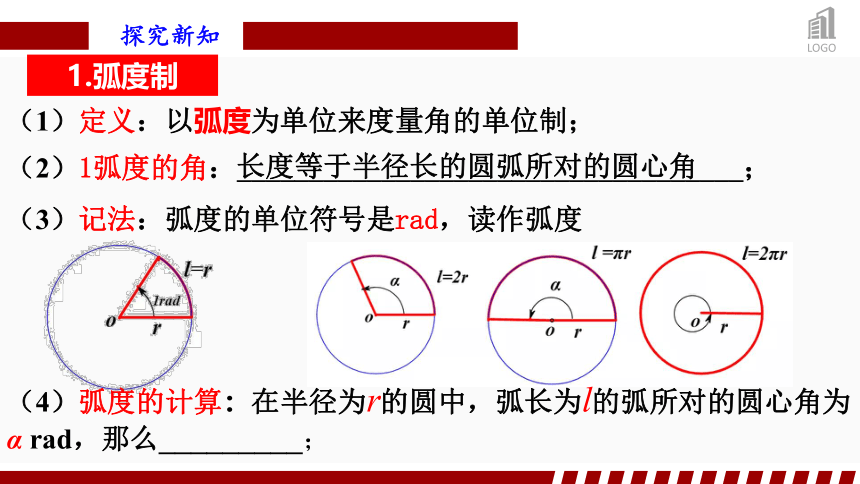
1.弧度制
(2)1弧度的角:___________________________________;
(3)记法:弧度的单位符号是rad,读作弧度
长度等于半径长的圆弧所对的圆心角
(1)定义:以弧度为单位来度量角的单位制;
(4)弧度的计算:在半径为r的圆中,弧长为l的弧所对的圆心角为α rad,那么_________;
探究新知
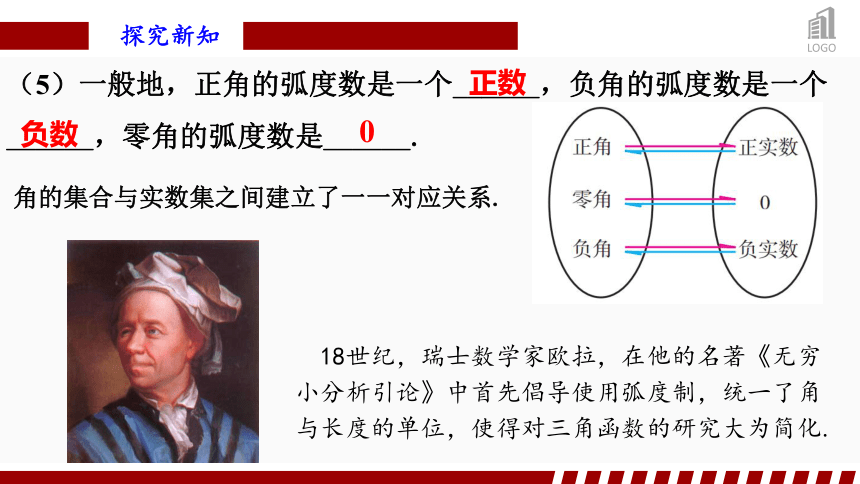
(5)一般地,正角的弧度数是一个______,负角的弧度数是一个______,零角的弧度数是______.
正数
负数
0
角的集合与实数集之间建立了一一对应关系.
18世纪,瑞士数学家欧拉,在他的名著《无穷小分析引论》中首先倡导使用弧度制,统一了角与长度的单位,使得对三角函数的研究大为简化.
探究新知
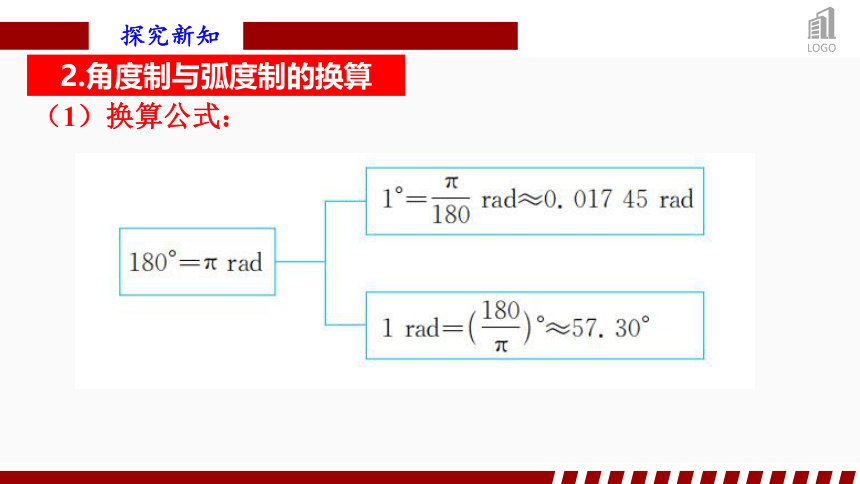
2.角度制与弧度制的换算
角度制、弧度制都是角的度量单位,它们之间如何换算呢?
1°等于多少弧度 1 rad又等于多少度呢?
探究新知
2.角度制与弧度制的换算
(1)换算公式:
例1
把下列角度化成弧度.
例2
把下列弧度化成角度.
题型一:角度制与弧度制的互化
(2)特殊角的弧度数与角度数对应表:
探究新知
(1)用角度表示
(2)用弧度表示
它们构成一个集合:
它们构成一个集合:
例3 终边相同的角的角度表示与弧度表示
课堂练习
3.用弧度表示终边落在如图所示阴影部分内的角θ的集合.
课堂练习
4.若角 的终边经过点P(-1,-1),则用弧度表示角 的集合是
.
第一象限角的集合:
第二象限角的集合:
第三象限角的集合:
第四象限角的集合:
5.使用弧度制,写出各象限角的集合:
3.扇形的弧长及面积公式
初中学的扇形弧长公式:
扇形面积公式:
例4
探究新知
3.扇形的弧长及面积公式
初中学的扇形弧长公式:
扇形面积公式:
l=|α|r
弧度制扇形弧长公式:
扇形面积公式:
例5 已知扇形圆心角为 ,面积为 ,则扇形的弧长等于( )
A. B. C. D.
【变式探究】一个扇形的弧长与面积的数值都是6,则这个扇形的圆心角是( )
A.1 B.2 C.3 D.4
题型二:弧长公式与扇形的面积公式的应用
金版140页例2
解:设扇形的半径为r,面积为S,弧长为l,圆心角为α(0<α<2π),
变式:已知扇形的周长是8 cm,当它的半径和圆心角各取什么值时,才能使扇形的面积最大?最大面积是多少?
解:设扇形的半径为r,面积为S,弧长为l,圆心角为α(0<α<2π),
课堂练习
1.角的度量有角度制和弧度制
2.角度和弧度的转换
3.弧度制下的弧长公式,面积公式
探究新知
练习
探究新知
练习
①
②
③
④
②
①
③
④
小技巧:a与a n所在象限的关系
n等分象限,逆向循环标记1—4,看a象限定区域。
5.1.2 弧度制
第五章 三角函数
姚明身高
姚明,
身高 7尺6寸,体重310磅;
英文名:Yao Ming
身高:226厘米
体重:134公斤
出生地点:上海
引 入
这种用度做单位来度量角的单位制叫做角度制.
1°=60′,1′=60″.
那些年 我们学习过了角度制,
在角度制中,1°角的规定_______________________________.
[答案] 将圆周分成360等份,一份弧所对的圆心角规定为1度角.
不同的单位制能给解决问题带来方便.
角的度量是否也能用不同的单位制呢?
能否像度量长度那样,用十进制的实数来度量角的大小呢?
思考: 能否计算?
探究新知
初中学习过的弧长公式:
已知射线OA,OA上有一点P,OA绕端点O旋转到OB,得到右图。
思考: 右图中涉及到哪些量?
这些量能不能用来度量角的大小?
这些量之间有什么关系?
探究新知
1.弧度制
(2)1弧度的角:___________________________________;
(3)记法:弧度的单位符号是rad,读作弧度
长度等于半径长的圆弧所对的圆心角
(1)定义:以弧度为单位来度量角的单位制;
(4)弧度的计算:在半径为r的圆中,弧长为l的弧所对的圆心角为α rad,那么_________;
探究新知
(5)一般地,正角的弧度数是一个______,负角的弧度数是一个______,零角的弧度数是______.
正数
负数
0
角的集合与实数集之间建立了一一对应关系.
18世纪,瑞士数学家欧拉,在他的名著《无穷小分析引论》中首先倡导使用弧度制,统一了角与长度的单位,使得对三角函数的研究大为简化.
探究新知
2.角度制与弧度制的换算
角度制、弧度制都是角的度量单位,它们之间如何换算呢?
1°等于多少弧度 1 rad又等于多少度呢?
探究新知
2.角度制与弧度制的换算
(1)换算公式:
例1
把下列角度化成弧度.
例2
把下列弧度化成角度.
题型一:角度制与弧度制的互化
(2)特殊角的弧度数与角度数对应表:
探究新知
(1)用角度表示
(2)用弧度表示
它们构成一个集合:
它们构成一个集合:
例3 终边相同的角的角度表示与弧度表示
课堂练习
3.用弧度表示终边落在如图所示阴影部分内的角θ的集合.
课堂练习
4.若角 的终边经过点P(-1,-1),则用弧度表示角 的集合是
.
第一象限角的集合:
第二象限角的集合:
第三象限角的集合:
第四象限角的集合:
5.使用弧度制,写出各象限角的集合:
3.扇形的弧长及面积公式
初中学的扇形弧长公式:
扇形面积公式:
例4
探究新知
3.扇形的弧长及面积公式
初中学的扇形弧长公式:
扇形面积公式:
l=|α|r
弧度制扇形弧长公式:
扇形面积公式:
例5 已知扇形圆心角为 ,面积为 ,则扇形的弧长等于( )
A. B. C. D.
【变式探究】一个扇形的弧长与面积的数值都是6,则这个扇形的圆心角是( )
A.1 B.2 C.3 D.4
题型二:弧长公式与扇形的面积公式的应用
金版140页例2
解:设扇形的半径为r,面积为S,弧长为l,圆心角为α(0<α<2π),
变式:已知扇形的周长是8 cm,当它的半径和圆心角各取什么值时,才能使扇形的面积最大?最大面积是多少?
解:设扇形的半径为r,面积为S,弧长为l,圆心角为α(0<α<2π),
课堂练习
1.角的度量有角度制和弧度制
2.角度和弧度的转换
3.弧度制下的弧长公式,面积公式
探究新知
练习
探究新知
练习
①
②
③
④
②
①
③
④
小技巧:a与a n所在象限的关系
n等分象限,逆向循环标记1—4,看a象限定区域。
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
