2.3 线段的长短课件(共27张PPT) 冀教版七年级数学上册
文档属性
| 名称 | 2.3 线段的长短课件(共27张PPT) 冀教版七年级数学上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 753.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-27 22:52:53 | ||
图片预览








文档简介
(共27张PPT)
第二章 几何图形的初步认识
2.3 线段的长短
1.借助“比身高”的情境,知道比较线段长短的方法.
2.会用直尺和圆规作一条线段等于已知线段.
3.知道两点之间的距离的概念及“两点之间的所有连线中,线段最短”的基本事实,并能应用它们解决问题.
◎重点:线段的性质及线段的比较方法,两点之间的距离的概念.
◎难点:比较线段的方法.
·导学建议·
教具准备:长方形纸片、三角形纸片、半透明的纸、绳子、圆规、直尺.
我们班谁最高?你们是怎么知道的?比较两个同学的身高,可以有几种方法?
比较线段的长短
·导学建议·
活动:①出示长方形纸片,教师用折叠的方法示范“比较相邻两边的长短”的方法;②出示三角形纸片,请一位同学上讲台用折叠的方法比较三边的长短;③在半透明的纸上画两条线段,剪下后请一位同学演示如何比较这两条线段的长短.完成上面的活动后,让学生用自己的语言叙述如何用叠合法比较线段长短.
阅读课本“大家谈谈”到“图2-3-4”前面的内容,完成下列问题.
如何比较线段AB,CD的长短?你有几种方法?
(1)测量法:用刻度尺分别量出两条线段的长度,长度大的线段较长,长度小的线段较短,长度相等时两线段一样长.
(2)叠合法:将线段AB放到线段CD上,使点A和点C重合,点B和点D在重合点的同侧.当点D在线段AB上时,AB>CD;当点B与D重合时,AB=CD;当点D在线段AB外时,AB<CD.
归纳总结:常用的比较线段长短的方法有 测量法 和 叠合法 .
测量法
叠合法
·导学建议·
如果有学生提到“估测法”,老师予以肯定,但要明确只有当线段的差别明显时,才能通过观察和估测比较长短.
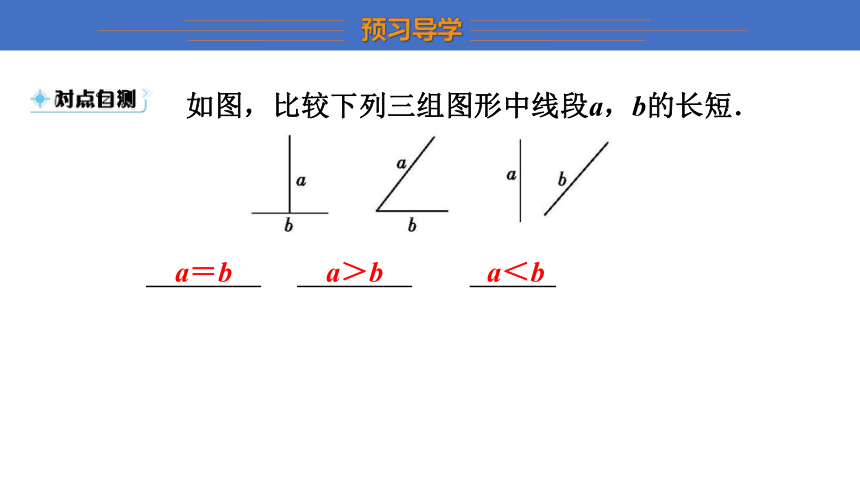
如图,比较下列三组图形中线段a,b的长短.
a=b a>b a<b
a=b
a>b
a<b
作一条线段等于已知线段
阅读课本“做一做”及其上面一段的内容,完成下列问题.
如图,已知线段a,求作一条线段,使它等于a. (作图工具:不带刻度的直尺和圆规)
如图,(1)画射线OA;(2)以O为圆心,a为半径画弧,交射线OA于点B,则线段OB即为所求.
·导学建议·
让学生自己先画,教师巡回检查.因为学生首次用圆规作图,所以教师需对学生加以指导,释疑解惑.最后教师总结作图的规范步骤.
归纳总结:用不带刻度的直尺和 圆规 可以作一条线段等于已知线段.
圆规
线段的基本事实
阅读课本“图2-3-5”后面的内容,完成下列问题.
1.基本事实:两点之间的所有连线中, 线段 最短.
2.两点之间线段的 长度 ,叫做两点之间的距离.
线段
长度
如图,从A点到B点有四条路线可以选择,一般情况下,你会选择路线 ② ,其中包含的数学道理是 两点之间的所有连线中,线段最短 .
②
两点之间
的所有连线中,线段最短
知识点一可以通过讨论比较身高的方法得出比较线段的方法,重点是叠合法.知识点二中的尺规作图,提醒学生注意保留作图痕迹.知识点三中“两点之间的距离”的定义要强调“线段的长度”而不是“线段”,这是学生易出错的地方.
·导学建议·
比较线段的长短
1.比较线段AB、AC、BC的长短,并用“<”连接.
解:AB<AC<BC.
2.常用的比较两条线段长度的方法有度量法和叠合法.如图,点C是线段AB上一点.请你利用直尺(不带刻度)和圆规应用叠合法,比较线段AC与BC的长短.(要求:保留作图痕迹)
解:如图,AC>BC.
【方法归纳交流】用叠合法比较线段的长短时,要注意两点:(1)两条线段的一个端点要 重合 ;(2)两条线段要在同一条直线(或射线)上,且在重合点的 同 侧.
重合
同
【变式演练】在跳绳比赛中,要在两条大绳中挑出一条较长的绳子用于比赛,选择的方法是( A )
A.把两条大绳的一端对齐,然后向一方拉直两根大绳,另一端在外面的即为长绳
B.把两条大绳接在一起
C.把两条大绳重合观察另一端的情况
D.没有办法挑选
A
线段的作图
3.如图,已知三角形ABC.
(1)读句画图:延长AB到D,使BD=AB;延长AC到E,使CE=AC;连接DE.
(2)测量DE和BC的长度,发现DE = BC.(填一个数)
(2)2.
解:(1)如图所示.
4.如图,O是线段AB上一点.
(1)读句画图:在线段AB上截取AP,使AP=OB;延长AB到D,使BD=OA.
(2)判断AO与BP,AB与OD,AO与OD的大小关系.
如何比较线段的长短?
用测量法和叠合法.
解:(1)如图所示.
(2)AO=BP,AB=OD,AO<OD.
·导学建议·
对于第4题第(2)问,可以选用测量法比较,也可以用圆规比较.教师可补充用圆规比较两条线段的方法.
“线段的基本事实”在生活中的应用
5.如图,A、B是河流l两旁的两个村庄,现要在河边建一个引水站向两村供水,问引水站建在什么地方才能使所需的管道最短?请在图中标出引水站的位置P,并说明你的理由.
解:如图,连接AB,与直线l相交于点P.理由:两点之间的所有连线中,线段最短.
线段的基本事实的应用
根据下列条件能判定A,B,C三点在同一直线上的是( B )
B
A.AB=3 cm,BC=4 cm,AC=5 cm
B.AB=6 cm,BC=2.5 cm,AC=3.5 cm
C.AB=5 cm,BC=10 cm,AC=6 cm
D.AB=14 cm,BC=7 cm,AC=8 cm
【方法归纳交流】当两条较短的线段之和等于 最长线段 的长度时,这三点在同一直线上,否则不在同一直线上.
最长线段
第二章 几何图形的初步认识
2.3 线段的长短
1.借助“比身高”的情境,知道比较线段长短的方法.
2.会用直尺和圆规作一条线段等于已知线段.
3.知道两点之间的距离的概念及“两点之间的所有连线中,线段最短”的基本事实,并能应用它们解决问题.
◎重点:线段的性质及线段的比较方法,两点之间的距离的概念.
◎难点:比较线段的方法.
·导学建议·
教具准备:长方形纸片、三角形纸片、半透明的纸、绳子、圆规、直尺.
我们班谁最高?你们是怎么知道的?比较两个同学的身高,可以有几种方法?
比较线段的长短
·导学建议·
活动:①出示长方形纸片,教师用折叠的方法示范“比较相邻两边的长短”的方法;②出示三角形纸片,请一位同学上讲台用折叠的方法比较三边的长短;③在半透明的纸上画两条线段,剪下后请一位同学演示如何比较这两条线段的长短.完成上面的活动后,让学生用自己的语言叙述如何用叠合法比较线段长短.
阅读课本“大家谈谈”到“图2-3-4”前面的内容,完成下列问题.
如何比较线段AB,CD的长短?你有几种方法?
(1)测量法:用刻度尺分别量出两条线段的长度,长度大的线段较长,长度小的线段较短,长度相等时两线段一样长.
(2)叠合法:将线段AB放到线段CD上,使点A和点C重合,点B和点D在重合点的同侧.当点D在线段AB上时,AB>CD;当点B与D重合时,AB=CD;当点D在线段AB外时,AB<CD.
归纳总结:常用的比较线段长短的方法有 测量法 和 叠合法 .
测量法
叠合法
·导学建议·
如果有学生提到“估测法”,老师予以肯定,但要明确只有当线段的差别明显时,才能通过观察和估测比较长短.
如图,比较下列三组图形中线段a,b的长短.
a=b a>b a<b
a=b
a>b
a<b
作一条线段等于已知线段
阅读课本“做一做”及其上面一段的内容,完成下列问题.
如图,已知线段a,求作一条线段,使它等于a. (作图工具:不带刻度的直尺和圆规)
如图,(1)画射线OA;(2)以O为圆心,a为半径画弧,交射线OA于点B,则线段OB即为所求.
·导学建议·
让学生自己先画,教师巡回检查.因为学生首次用圆规作图,所以教师需对学生加以指导,释疑解惑.最后教师总结作图的规范步骤.
归纳总结:用不带刻度的直尺和 圆规 可以作一条线段等于已知线段.
圆规
线段的基本事实
阅读课本“图2-3-5”后面的内容,完成下列问题.
1.基本事实:两点之间的所有连线中, 线段 最短.
2.两点之间线段的 长度 ,叫做两点之间的距离.
线段
长度
如图,从A点到B点有四条路线可以选择,一般情况下,你会选择路线 ② ,其中包含的数学道理是 两点之间的所有连线中,线段最短 .
②
两点之间
的所有连线中,线段最短
知识点一可以通过讨论比较身高的方法得出比较线段的方法,重点是叠合法.知识点二中的尺规作图,提醒学生注意保留作图痕迹.知识点三中“两点之间的距离”的定义要强调“线段的长度”而不是“线段”,这是学生易出错的地方.
·导学建议·
比较线段的长短
1.比较线段AB、AC、BC的长短,并用“<”连接.
解:AB<AC<BC.
2.常用的比较两条线段长度的方法有度量法和叠合法.如图,点C是线段AB上一点.请你利用直尺(不带刻度)和圆规应用叠合法,比较线段AC与BC的长短.(要求:保留作图痕迹)
解:如图,AC>BC.
【方法归纳交流】用叠合法比较线段的长短时,要注意两点:(1)两条线段的一个端点要 重合 ;(2)两条线段要在同一条直线(或射线)上,且在重合点的 同 侧.
重合
同
【变式演练】在跳绳比赛中,要在两条大绳中挑出一条较长的绳子用于比赛,选择的方法是( A )
A.把两条大绳的一端对齐,然后向一方拉直两根大绳,另一端在外面的即为长绳
B.把两条大绳接在一起
C.把两条大绳重合观察另一端的情况
D.没有办法挑选
A
线段的作图
3.如图,已知三角形ABC.
(1)读句画图:延长AB到D,使BD=AB;延长AC到E,使CE=AC;连接DE.
(2)测量DE和BC的长度,发现DE = BC.(填一个数)
(2)2.
解:(1)如图所示.
4.如图,O是线段AB上一点.
(1)读句画图:在线段AB上截取AP,使AP=OB;延长AB到D,使BD=OA.
(2)判断AO与BP,AB与OD,AO与OD的大小关系.
如何比较线段的长短?
用测量法和叠合法.
解:(1)如图所示.
(2)AO=BP,AB=OD,AO<OD.
·导学建议·
对于第4题第(2)问,可以选用测量法比较,也可以用圆规比较.教师可补充用圆规比较两条线段的方法.
“线段的基本事实”在生活中的应用
5.如图,A、B是河流l两旁的两个村庄,现要在河边建一个引水站向两村供水,问引水站建在什么地方才能使所需的管道最短?请在图中标出引水站的位置P,并说明你的理由.
解:如图,连接AB,与直线l相交于点P.理由:两点之间的所有连线中,线段最短.
线段的基本事实的应用
根据下列条件能判定A,B,C三点在同一直线上的是( B )
B
A.AB=3 cm,BC=4 cm,AC=5 cm
B.AB=6 cm,BC=2.5 cm,AC=3.5 cm
C.AB=5 cm,BC=10 cm,AC=6 cm
D.AB=14 cm,BC=7 cm,AC=8 cm
【方法归纳交流】当两条较短的线段之和等于 最长线段 的长度时,这三点在同一直线上,否则不在同一直线上.
最长线段
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
