2.8 平面图形的旋转 课件(共25张PPT)冀教版七年级上册数学
文档属性
| 名称 | 2.8 平面图形的旋转 课件(共25张PPT)冀教版七年级上册数学 |

|
|
| 格式 | pptx | ||
| 文件大小 | 844.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-27 23:03:40 | ||
图片预览








文档简介
(共25张PPT)
第二章 几何图形的初步认识
2.8 平面图形的旋转
1.结合具体实例认识旋转的概念.
2.经历探索和操作,发现并熟记图形旋转的性质.
3.能够按要求作出简单平面图形旋转后的图形.
◎重点:平面图形旋转的性质及其应用.
◎难点:作简单平面图形旋转后的图形.
我们生活在一个充满旋转的世界里,例如:正在转动的钟表时针、电风扇的叶片、汽车的雨刷,你还能举出生活中旋转的例子吗?你是否思考过以上情景中的转动现象有什么共同特征?
旋转的有关概念
阅读课本“观察与思考”,完成下列问题.
1.在课本“图2-8-1”中,说说∠AOB可以看作由射线OA经过怎样的旋转形成的?
由射线OA绕端点O按逆时针方向旋转到OB的位置形成的.
2.在课本“图2-8-2”中,说说线段CD可以看作由线段AB经过怎样的旋转得到的?点A、B的对应点分别是哪个?
由线段AB绕点O按顺时针方向旋转到CD的位置.点A的对应点是点C,点B的对应点是点D.
3.描述一个图形的旋转要注意哪几点?
三点:旋转中心、旋转方向、旋转角度.
归纳总结:在平面内,一个图形绕一个 定点 沿某个 方向 转过一个 角度 ,这样的图形运动叫做旋转.这个 定点 叫做旋转中心, 转过的这个角 叫做旋转角.
·导学建议·
定点
方向
角度
定点
转过的这个角
1.可让学生通过观察、操作与思考,用自己的语言描绘旋转的特征.
2.教师强调描述旋转时,注意三要素:旋转中心、旋转方向、旋转角度.
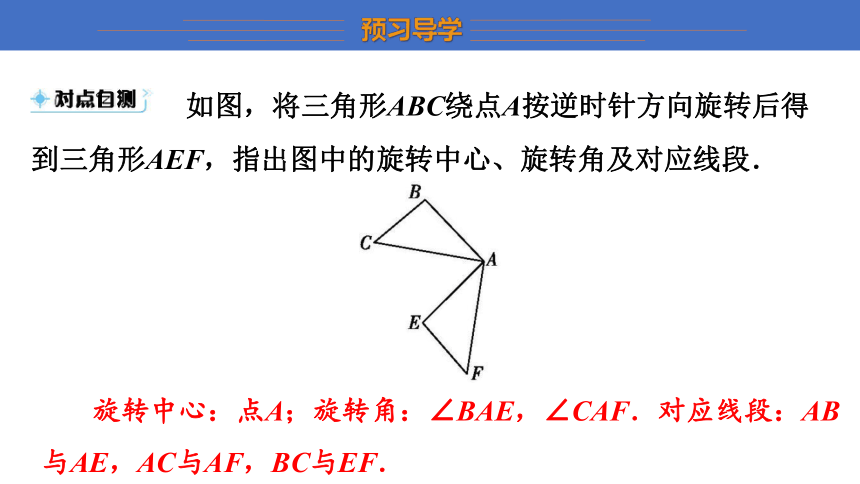
如图,将三角形ABC绕点A按逆时针方向旋转后得到三角形AEF,指出图中的旋转中心、旋转角及对应线段.
旋转中心:点A;旋转角:∠BAE,∠CAF.对应线段:AB与AE,AC与AF,BC与EF.
旋转的性质
阅读课本“一起探究”,交流下面的问题.
1.在课本“图2-8-3”中如何找点A、B的对应点?
在ON上截取OA',使OA'=OA;在ON上截取OB',使OB'=OB.点A'、B'即为点A、B的对应点.
2.指出课本“图2-8-4”中的旋转中心、旋转角及对应线段、对应角,并说出对应线段、对应角分别有什么数量关系?
旋转中心是点O,∠BOD和∠AOC都是旋转角,对应线段:AB和CD,OA和OC,OB和OD;对应角:∠B和∠D,∠A和∠C,∠AOB和∠COD,它们分别相等.
旋转中心是点O,∠BOD和∠AOC都是旋转角,对应线
段:AB和CD,OA和OC,OB和OD;对应角:∠B和∠D,∠A
和∠C,∠AOB和∠COD,它们分别相等.
归纳总结:在平面内,一个图形旋转后得到的图形与原来的图形之间有如下结果:对应点到旋转中心的距离 相等 ;每对对应点与旋转中心连线所成的角都是 相等 的角,它们都等于 旋转角 .
相等
相等
旋转角
对于平面图形旋转性质的研究,应当紧紧抓住一对对应点之间经旋转的变化路径,即以旋转中心为圆心,以原来那个点与旋转中心连线的线段为半径,旋转的角度等于旋转角.
·导学建议·
如图,点A、B、C、D都在方格纸的格点上,若三角形AOB绕点O按逆时针方向旋转到三角形COD的位置,则旋转的角度为( C )
A.30° B.45° C.90° D.135°
C
旋转现象
1.下列运动属于旋转的是( B )
A.车轮在水平地面上滚动 B.方向盘的转动
C.气球升空的运动 D.火车车厢的直线运动
B
2.如图,在正方形网格中,将三角形ABC绕点A旋转后得到三角形ADE.下列旋转方式中,符合题意的是( B )
A.顺时针旋转90°
B.逆时针旋转90°
C.顺时针旋转45°
D.逆时针旋转45°
B
旋转性质的应用
3.如图,三角形ABO绕点O旋转得到三角形CDO,在这个旋转过程中:
(1)旋转中心是 点O ,旋转角是 ∠AOC 或 ∠BOD ;
点O
∠AOC
∠BOD
(2)经过旋转,点A旋转到了 点C ,点B旋转到了 点D ;
(3)如果AO=4 cm,那么CO= 4 cm ;
(4)如果AB=1 cm,那么CD= 1 cm ;
(5)如果∠AOC=60°,∠AOB=20°,那么∠BOD= 60° ,∠COD= 20° ,∠BOC= 40° .
点C
点
D
4 cm
1 cm
60°
20°
40°
4.如图,将三角形ABC绕着点C顺时针旋转50°后得到三角形A'B'C,若∠B'CA'=30°,则∠BCA'的度数是( B )
A.90° B.80° C.40° D.30°
B
【变式演练】某图形中的一个长方形是另一个长方形按顺时针方向旋转90°形成的是( A )
A
旋转作图
5.如图,在由边长为1的小正方形组成的网格中,三角形ABC的顶点均落在格点上,将三角形ABC绕点O顺时针旋转90°后,得到三角形A1B1C1,在网格图中画出三角形A1B1C1.
画旋转后的图形需要先画出哪些点?
需要先画出各顶点的对应点.
解:如图.
【方法归纳交流】画已知图形旋转后的图形时,先弄清 旋转中心 、 旋转方向 、 旋转角度 ,再根据对应点与旋转中心的连线所成的角等于 旋转角 ,对应点到旋转中心的距离 相等 ,确定一些对应点的位置,最后连线.
旋转中心
旋转方向
旋转角度
旋转角
相等
如图,如果正方形CDEF旋转后能与正方形ABCD重合,那么图形所在的平面上可以作为旋转中心的点共有几个?请你说出这些点的位置,并说明正方形CDEF是如何绕这些点旋转后与正方形ABCD重合的.
解:3个,它们分别是点D、点C、线段CD的中点.
正方形CDEF绕点D顺时针旋转90°与正方形ABCD重合;正方形CDEF绕点C逆时针旋转90°与正方形ABCD重合;正方形CDEF绕CD的中点逆时针(或顺时针)旋转180°后与正方形ABCD重合.
课程结束前可布置一项创意作业——创意比拼:请同学们用旋转的知识为我们校园的操场设计一个花台.可由几位同学一起完成,下节课中展示同学们的作品.
·导学建议·
第二章 几何图形的初步认识
2.8 平面图形的旋转
1.结合具体实例认识旋转的概念.
2.经历探索和操作,发现并熟记图形旋转的性质.
3.能够按要求作出简单平面图形旋转后的图形.
◎重点:平面图形旋转的性质及其应用.
◎难点:作简单平面图形旋转后的图形.
我们生活在一个充满旋转的世界里,例如:正在转动的钟表时针、电风扇的叶片、汽车的雨刷,你还能举出生活中旋转的例子吗?你是否思考过以上情景中的转动现象有什么共同特征?
旋转的有关概念
阅读课本“观察与思考”,完成下列问题.
1.在课本“图2-8-1”中,说说∠AOB可以看作由射线OA经过怎样的旋转形成的?
由射线OA绕端点O按逆时针方向旋转到OB的位置形成的.
2.在课本“图2-8-2”中,说说线段CD可以看作由线段AB经过怎样的旋转得到的?点A、B的对应点分别是哪个?
由线段AB绕点O按顺时针方向旋转到CD的位置.点A的对应点是点C,点B的对应点是点D.
3.描述一个图形的旋转要注意哪几点?
三点:旋转中心、旋转方向、旋转角度.
归纳总结:在平面内,一个图形绕一个 定点 沿某个 方向 转过一个 角度 ,这样的图形运动叫做旋转.这个 定点 叫做旋转中心, 转过的这个角 叫做旋转角.
·导学建议·
定点
方向
角度
定点
转过的这个角
1.可让学生通过观察、操作与思考,用自己的语言描绘旋转的特征.
2.教师强调描述旋转时,注意三要素:旋转中心、旋转方向、旋转角度.
如图,将三角形ABC绕点A按逆时针方向旋转后得到三角形AEF,指出图中的旋转中心、旋转角及对应线段.
旋转中心:点A;旋转角:∠BAE,∠CAF.对应线段:AB与AE,AC与AF,BC与EF.
旋转的性质
阅读课本“一起探究”,交流下面的问题.
1.在课本“图2-8-3”中如何找点A、B的对应点?
在ON上截取OA',使OA'=OA;在ON上截取OB',使OB'=OB.点A'、B'即为点A、B的对应点.
2.指出课本“图2-8-4”中的旋转中心、旋转角及对应线段、对应角,并说出对应线段、对应角分别有什么数量关系?
旋转中心是点O,∠BOD和∠AOC都是旋转角,对应线段:AB和CD,OA和OC,OB和OD;对应角:∠B和∠D,∠A和∠C,∠AOB和∠COD,它们分别相等.
旋转中心是点O,∠BOD和∠AOC都是旋转角,对应线
段:AB和CD,OA和OC,OB和OD;对应角:∠B和∠D,∠A
和∠C,∠AOB和∠COD,它们分别相等.
归纳总结:在平面内,一个图形旋转后得到的图形与原来的图形之间有如下结果:对应点到旋转中心的距离 相等 ;每对对应点与旋转中心连线所成的角都是 相等 的角,它们都等于 旋转角 .
相等
相等
旋转角
对于平面图形旋转性质的研究,应当紧紧抓住一对对应点之间经旋转的变化路径,即以旋转中心为圆心,以原来那个点与旋转中心连线的线段为半径,旋转的角度等于旋转角.
·导学建议·
如图,点A、B、C、D都在方格纸的格点上,若三角形AOB绕点O按逆时针方向旋转到三角形COD的位置,则旋转的角度为( C )
A.30° B.45° C.90° D.135°
C
旋转现象
1.下列运动属于旋转的是( B )
A.车轮在水平地面上滚动 B.方向盘的转动
C.气球升空的运动 D.火车车厢的直线运动
B
2.如图,在正方形网格中,将三角形ABC绕点A旋转后得到三角形ADE.下列旋转方式中,符合题意的是( B )
A.顺时针旋转90°
B.逆时针旋转90°
C.顺时针旋转45°
D.逆时针旋转45°
B
旋转性质的应用
3.如图,三角形ABO绕点O旋转得到三角形CDO,在这个旋转过程中:
(1)旋转中心是 点O ,旋转角是 ∠AOC 或 ∠BOD ;
点O
∠AOC
∠BOD
(2)经过旋转,点A旋转到了 点C ,点B旋转到了 点D ;
(3)如果AO=4 cm,那么CO= 4 cm ;
(4)如果AB=1 cm,那么CD= 1 cm ;
(5)如果∠AOC=60°,∠AOB=20°,那么∠BOD= 60° ,∠COD= 20° ,∠BOC= 40° .
点C
点
D
4 cm
1 cm
60°
20°
40°
4.如图,将三角形ABC绕着点C顺时针旋转50°后得到三角形A'B'C,若∠B'CA'=30°,则∠BCA'的度数是( B )
A.90° B.80° C.40° D.30°
B
【变式演练】某图形中的一个长方形是另一个长方形按顺时针方向旋转90°形成的是( A )
A
旋转作图
5.如图,在由边长为1的小正方形组成的网格中,三角形ABC的顶点均落在格点上,将三角形ABC绕点O顺时针旋转90°后,得到三角形A1B1C1,在网格图中画出三角形A1B1C1.
画旋转后的图形需要先画出哪些点?
需要先画出各顶点的对应点.
解:如图.
【方法归纳交流】画已知图形旋转后的图形时,先弄清 旋转中心 、 旋转方向 、 旋转角度 ,再根据对应点与旋转中心的连线所成的角等于 旋转角 ,对应点到旋转中心的距离 相等 ,确定一些对应点的位置,最后连线.
旋转中心
旋转方向
旋转角度
旋转角
相等
如图,如果正方形CDEF旋转后能与正方形ABCD重合,那么图形所在的平面上可以作为旋转中心的点共有几个?请你说出这些点的位置,并说明正方形CDEF是如何绕这些点旋转后与正方形ABCD重合的.
解:3个,它们分别是点D、点C、线段CD的中点.
正方形CDEF绕点D顺时针旋转90°与正方形ABCD重合;正方形CDEF绕点C逆时针旋转90°与正方形ABCD重合;正方形CDEF绕CD的中点逆时针(或顺时针)旋转180°后与正方形ABCD重合.
课程结束前可布置一项创意作业——创意比拼:请同学们用旋转的知识为我们校园的操场设计一个花台.可由几位同学一起完成,下节课中展示同学们的作品.
·导学建议·
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
