3.2 代数式 第2课时课件(共25张PPT) 冀教版七年级上册数学
文档属性
| 名称 | 3.2 代数式 第2课时课件(共25张PPT) 冀教版七年级上册数学 |

|
|
| 格式 | pptx | ||
| 文件大小 | 832.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-27 23:07:39 | ||
图片预览








文档简介
(共25张PPT)
第三章 代数式
3.2 代数式 第2课时
1.能分析简单问题的数量关系,并用代数式表示出来.
2.进一步熟悉代数式的书写要求.
◎重点:把实际问题中的数量关系列成代数式.
◎难点:正确理解题意,找出数量关系里的运算顺序并能准确地写成代数式.
数学也含有相当的艺术成分,将数学与诗歌融于一体,读来朗朗上口,形成诗歌海洋中别具一格的浪花,也是数学天空中闪耀的繁星.下面请同学们欣赏一首数学诗:甲乙两个售货员,推销同种健身圈.甲售一个赚五元,乙售一个赚八元.甲售十个乙八个,所得货款共几何?设定进价是x元,列出代数式来算.
答案:10(x+5)+8(x+8) .
用代数式表示实际问题中的数量关系
1.仔细分析课本本课时“一起探究”的2个题目,完成下面的表格,初步体会实际问题数学化的过程.
第1题:
桶和油的质量(千克) 油的质量(千克) 桶的质量(千克)
装满油 a c a-c
油用去一半 b b-
a
c
a-c
b
b-
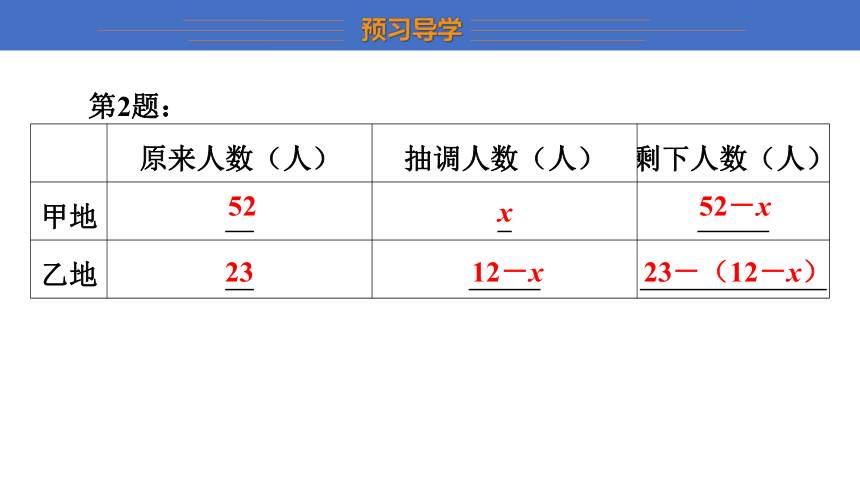
原来人数(人) 抽调人数(人) 剩下人数(人)
甲地 52 x 52-x
乙地 23 12-x 23-(12-x)
52
x
52-x
23
12-x
23-(12-x)
第2题:
对于第2题,学生若采用两地共75人,调走12人,剩余63人,甲地剩余(52-x)人,则乙地剩余[63-(52-x)]人来列代数式的话,教师要对学生的做法加以肯定,并指出用不同的代数式表示同一个量,是解决实际问题的一种常用方法.
·导学建议·
2.完成课本本课时“做一做”, 再次体会实际问题数学化的过程.
(1)85x.(2)0.8x.(3)380x.(4)5×5.6%x,x+5×5.6%x.(5)x.
归纳总结:实际问题中的一些基本数量关系.
(1)行程问题:路程= 速度×时间 .
速度×时间
(2)商品销售问题:总价= 单价×数量 ;利润= 售价-进价 .
(3)利息问题:利息= 本金×利率×期数 ,本息= 本金+利息 .
(4)工程问题:工作总量= 工作效率×工作时间 .(若工作总量不明确,则把它当作整体“1”)
单价×数量
售
价-进价
本金×利率×期数
本金+利息
工作效率×工作时
间
预习导学部分建议教师用10分钟左右的时间让学生独立完成,再用2分钟左右的时间集体订正,注意提醒学生当实际问题中写出的式子后面带有单位时,如果式子是和或差的形式,那么要将式子添加括号.通过该知识点的学习,让学生能分析简单问题的数量关系,达成目标1和目标2的教学.
·导学建议·
参观李大钊纪念馆,学习列代数式
1.今天我们一起去参观李大钊纪念馆,边参观边解决一些数学问题.
李大钊纪念馆 李大钊故居
(1)李大钊纪念馆距学校s千米,校车的速度为40千米/时,到达纪念馆需要 小时.
(2)李大钊生平事迹陈列厅呈长方形,长m米,宽n米,共展出李大钊展品2p件,陈列厅占地面积有 mn 平方米, 平均每平方米展出了 件展品.
mn
(3)参观完纪念馆后大家乘校车去李大钊故居,校车以50千米/时的速度行驶,计划t小时后到李大钊故居,现因道路通畅,校车的速度增加v千米/时,那么到李大钊故居需要 小时.
(4)参观完纪念馆后,李老师乘出租车去教育局.已知出租车收费标准为起步价7元,3千米后每千米1.4元,则李老师乘出租车x(x>3)千米应付款 [7+1.4(x-3)] 元.
【方法归纳交流】列代数式表示数量关系,其关键是把实际问题中的数量关系抽象为 和、差、倍、分 的关系.
[7+1.4(x-3)]
和、差、倍、分
与商品销售有关的问题
2.一箱水果的进价为a元,每个月销量为30箱.
(1)若利润率为15%,则每箱的售价为 (a+15%a)或(1+15%)a 元,月利润为 30×15%a 元.
(2)若售价为n元,则每个月的营业额为 30n 元;月利润为 30(n-a)或(30n-30a) .
(a+15%a)或
(1+15%)a
30×15%a
30n
30(n-a)或(30n-30a)
(3)若在原价n元的基础上打六折销售,则每箱售价为 60%n 元,月利润为 30(60%n-a) 元.
【变式拓展】某商店对某种商品调价,按原价的八折出售,打折后的利润率是20%,已知该商品的原价是63元,设该商品的进价是x元,请用两种方法写出表示该商品实际售价的代数式.
60%n
30(60%n-a)
解:方法一:63×80%元;方法二:(x+20%x)元或(1+20%)x元.
【方法归纳交流】商品的售价= 原价 ×折扣=进价+ 进价 ×实际利率.
原价
进价
与电费有关的问题
3.小明家所在小区的一则关于电费的通知内容如下:我小区供电公司从9月份起实行分时电价:执行时段分为平、谷两个时段,平段为8:00—22:00,14小时,谷段为22:00—次日8:00,10小时.平段用电价格在原销售电价a元的基础上每千瓦时上浮0.03元,谷段电价在原销售电价基础上每千瓦时下浮0.25元.小明家9月份平段电量40千瓦时, 谷段电量60千瓦时.
(2)如不使用分时电价结算, 9月份他家将多支付电费多少元?
解:(1)[40(a+0.03)+60(a-0.25)]元.
(2)100a-[40(a+0.03)+60(a-0.25)]或13.8元.
(1)问他家该月应付电费多少元?
与水费有关的问题
4.看水费价目表,完成下面的填空题:
(1)8月用水量为5 m3,则应收费 5a 元.
(2)9月用水量为9 m3,则应收费 [6a +(9-6)c] 元.
(3)10月用水量为x m3(x>10),则应收费 [6a+(10-6)c+5(x -10)] 元.
5a
[6a +(9-6)c]
[6a+(10
-6)c+5(x -10)]
10月份的用水量应该分为几段来算?
三段.
·导学建议·
教师可事先让学生收集其小区的水费或电费收费标准,并设计成问题,同桌交换完成,让学生体会生活中处处有数学.
赏数学诗,列代数式
在我国古代许多数学著作中都可以看到以诗歌形式给出的数学问题及其解答.这些诗歌融文、史、数、谜于一体,读来朗朗上口,给枯燥的数学增添了鲜活、生动的元素.
(一)塔顶几盏灯
远望巍巍塔七层, 红光点点倍加增.共灯三百八十一,请问塔尖几盏灯.
赏析:诗的大意是有一座高大雄伟的宝塔,共有七层,每层都挂着红红的大灯笼,虽然不知道各层灯笼的数量是多少,但知道从上到下的第二层开始,每层的盏数都是上一层的2 倍,并知道总共有灯381 盏.问:这个宝塔每层各有多少盏灯?
若设顶层有灯 x 盏,请用含x的代数式表示这381盏灯.
解:x+2x+4x+8x+16x+32x+64x.
(二)李三公开店
我问开店李三公,多少客人在店中?一房七客多七客,一房九客一房空.
赏析:诗的大意是我问开店的李三公有多少客人住在店里,李三公回答说:“如果一个房间里住7人,那么余下7人没处住;如果一个房间住9人,那么又正好空出一个房间.
设店里有x个房间,请用两种方法表示住店的人数.
解:方法一:7x+7;方法二:9(x-1).
·导学建议·
本节课以数学诗开始,又以数学诗结束,首尾呼应,让学生体会数学的艺术美.合作探究建议用20分钟左右的时间完成,其中任务驱动一、二可让学生独立完成,任务驱动三的第2问可以让学生展开讨论,任务驱动四可换用学生收集的收费标准来展开探讨.备选问题根据学情选用.
第三章 代数式
3.2 代数式 第2课时
1.能分析简单问题的数量关系,并用代数式表示出来.
2.进一步熟悉代数式的书写要求.
◎重点:把实际问题中的数量关系列成代数式.
◎难点:正确理解题意,找出数量关系里的运算顺序并能准确地写成代数式.
数学也含有相当的艺术成分,将数学与诗歌融于一体,读来朗朗上口,形成诗歌海洋中别具一格的浪花,也是数学天空中闪耀的繁星.下面请同学们欣赏一首数学诗:甲乙两个售货员,推销同种健身圈.甲售一个赚五元,乙售一个赚八元.甲售十个乙八个,所得货款共几何?设定进价是x元,列出代数式来算.
答案:10(x+5)+8(x+8) .
用代数式表示实际问题中的数量关系
1.仔细分析课本本课时“一起探究”的2个题目,完成下面的表格,初步体会实际问题数学化的过程.
第1题:
桶和油的质量(千克) 油的质量(千克) 桶的质量(千克)
装满油 a c a-c
油用去一半 b b-
a
c
a-c
b
b-
原来人数(人) 抽调人数(人) 剩下人数(人)
甲地 52 x 52-x
乙地 23 12-x 23-(12-x)
52
x
52-x
23
12-x
23-(12-x)
第2题:
对于第2题,学生若采用两地共75人,调走12人,剩余63人,甲地剩余(52-x)人,则乙地剩余[63-(52-x)]人来列代数式的话,教师要对学生的做法加以肯定,并指出用不同的代数式表示同一个量,是解决实际问题的一种常用方法.
·导学建议·
2.完成课本本课时“做一做”, 再次体会实际问题数学化的过程.
(1)85x.(2)0.8x.(3)380x.(4)5×5.6%x,x+5×5.6%x.(5)x.
归纳总结:实际问题中的一些基本数量关系.
(1)行程问题:路程= 速度×时间 .
速度×时间
(2)商品销售问题:总价= 单价×数量 ;利润= 售价-进价 .
(3)利息问题:利息= 本金×利率×期数 ,本息= 本金+利息 .
(4)工程问题:工作总量= 工作效率×工作时间 .(若工作总量不明确,则把它当作整体“1”)
单价×数量
售
价-进价
本金×利率×期数
本金+利息
工作效率×工作时
间
预习导学部分建议教师用10分钟左右的时间让学生独立完成,再用2分钟左右的时间集体订正,注意提醒学生当实际问题中写出的式子后面带有单位时,如果式子是和或差的形式,那么要将式子添加括号.通过该知识点的学习,让学生能分析简单问题的数量关系,达成目标1和目标2的教学.
·导学建议·
参观李大钊纪念馆,学习列代数式
1.今天我们一起去参观李大钊纪念馆,边参观边解决一些数学问题.
李大钊纪念馆 李大钊故居
(1)李大钊纪念馆距学校s千米,校车的速度为40千米/时,到达纪念馆需要 小时.
(2)李大钊生平事迹陈列厅呈长方形,长m米,宽n米,共展出李大钊展品2p件,陈列厅占地面积有 mn 平方米, 平均每平方米展出了 件展品.
mn
(3)参观完纪念馆后大家乘校车去李大钊故居,校车以50千米/时的速度行驶,计划t小时后到李大钊故居,现因道路通畅,校车的速度增加v千米/时,那么到李大钊故居需要 小时.
(4)参观完纪念馆后,李老师乘出租车去教育局.已知出租车收费标准为起步价7元,3千米后每千米1.4元,则李老师乘出租车x(x>3)千米应付款 [7+1.4(x-3)] 元.
【方法归纳交流】列代数式表示数量关系,其关键是把实际问题中的数量关系抽象为 和、差、倍、分 的关系.
[7+1.4(x-3)]
和、差、倍、分
与商品销售有关的问题
2.一箱水果的进价为a元,每个月销量为30箱.
(1)若利润率为15%,则每箱的售价为 (a+15%a)或(1+15%)a 元,月利润为 30×15%a 元.
(2)若售价为n元,则每个月的营业额为 30n 元;月利润为 30(n-a)或(30n-30a) .
(a+15%a)或
(1+15%)a
30×15%a
30n
30(n-a)或(30n-30a)
(3)若在原价n元的基础上打六折销售,则每箱售价为 60%n 元,月利润为 30(60%n-a) 元.
【变式拓展】某商店对某种商品调价,按原价的八折出售,打折后的利润率是20%,已知该商品的原价是63元,设该商品的进价是x元,请用两种方法写出表示该商品实际售价的代数式.
60%n
30(60%n-a)
解:方法一:63×80%元;方法二:(x+20%x)元或(1+20%)x元.
【方法归纳交流】商品的售价= 原价 ×折扣=进价+ 进价 ×实际利率.
原价
进价
与电费有关的问题
3.小明家所在小区的一则关于电费的通知内容如下:我小区供电公司从9月份起实行分时电价:执行时段分为平、谷两个时段,平段为8:00—22:00,14小时,谷段为22:00—次日8:00,10小时.平段用电价格在原销售电价a元的基础上每千瓦时上浮0.03元,谷段电价在原销售电价基础上每千瓦时下浮0.25元.小明家9月份平段电量40千瓦时, 谷段电量60千瓦时.
(2)如不使用分时电价结算, 9月份他家将多支付电费多少元?
解:(1)[40(a+0.03)+60(a-0.25)]元.
(2)100a-[40(a+0.03)+60(a-0.25)]或13.8元.
(1)问他家该月应付电费多少元?
与水费有关的问题
4.看水费价目表,完成下面的填空题:
(1)8月用水量为5 m3,则应收费 5a 元.
(2)9月用水量为9 m3,则应收费 [6a +(9-6)c] 元.
(3)10月用水量为x m3(x>10),则应收费 [6a+(10-6)c+5(x -10)] 元.
5a
[6a +(9-6)c]
[6a+(10
-6)c+5(x -10)]
10月份的用水量应该分为几段来算?
三段.
·导学建议·
教师可事先让学生收集其小区的水费或电费收费标准,并设计成问题,同桌交换完成,让学生体会生活中处处有数学.
赏数学诗,列代数式
在我国古代许多数学著作中都可以看到以诗歌形式给出的数学问题及其解答.这些诗歌融文、史、数、谜于一体,读来朗朗上口,给枯燥的数学增添了鲜活、生动的元素.
(一)塔顶几盏灯
远望巍巍塔七层, 红光点点倍加增.共灯三百八十一,请问塔尖几盏灯.
赏析:诗的大意是有一座高大雄伟的宝塔,共有七层,每层都挂着红红的大灯笼,虽然不知道各层灯笼的数量是多少,但知道从上到下的第二层开始,每层的盏数都是上一层的2 倍,并知道总共有灯381 盏.问:这个宝塔每层各有多少盏灯?
若设顶层有灯 x 盏,请用含x的代数式表示这381盏灯.
解:x+2x+4x+8x+16x+32x+64x.
(二)李三公开店
我问开店李三公,多少客人在店中?一房七客多七客,一房九客一房空.
赏析:诗的大意是我问开店的李三公有多少客人住在店里,李三公回答说:“如果一个房间里住7人,那么余下7人没处住;如果一个房间住9人,那么又正好空出一个房间.
设店里有x个房间,请用两种方法表示住店的人数.
解:方法一:7x+7;方法二:9(x-1).
·导学建议·
本节课以数学诗开始,又以数学诗结束,首尾呼应,让学生体会数学的艺术美.合作探究建议用20分钟左右的时间完成,其中任务驱动一、二可让学生独立完成,任务驱动三的第2问可以让学生展开讨论,任务驱动四可换用学生收集的收费标准来展开探讨.备选问题根据学情选用.
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
