3.2 代数式 第4课时课件(共24张PPT) 冀教版七年级上册数学
文档属性
| 名称 | 3.2 代数式 第4课时课件(共24张PPT) 冀教版七年级上册数学 |

|
|
| 格式 | pptx | ||
| 文件大小 | 850.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-27 23:08:43 | ||
图片预览







文档简介
(共24张PPT)
第三章 代数式
3.2 代数式 第4课时
1.会探索数学规律,列出代数式.
2.学会转化思想与化归思想.
◎重点:能探索发现数学规律并能正确验证.
◎难点:探索发现数学规律.
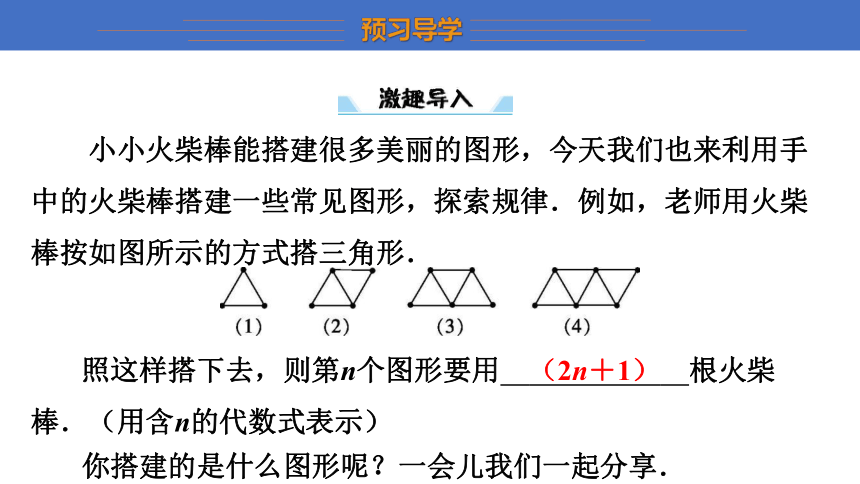
小小火柴棒能搭建很多美丽的图形,今天我们也来利用手中的火柴棒搭建一些常见图形,探索规律.例如,老师用火柴棒按如图所示的方式搭三角形.
照这样搭下去,则第n个图形要用 (2n+1) 根火柴棒.(用含n的代数式表示)
(2n+1)
你搭建的是什么图形呢?一会儿我们一起分享.
探索数字规律列代数式
完成课本本课时“一起探究”中的“数阵”问题,感受数字的规律探索,并完成下列各题.
1.找到数字15,并把它周围的8个数字填在表(1)中.
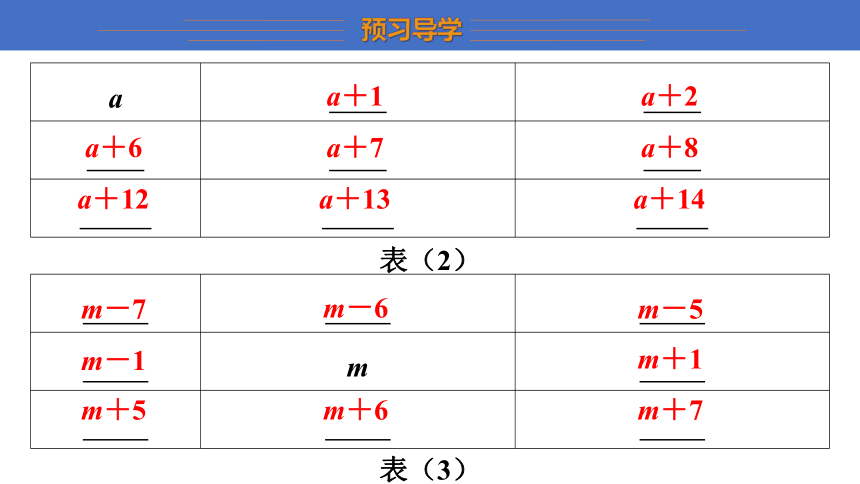
2.设方框左上角的数字为a,用含a的代数式表示其他8个数字并填在表(2)中,用含a的代数式表示这9个数的和为 9a+63 .
9a+
63
3.设方框正中间的数字为m,请用含m的代数式表示其他的8个数并填在表(3)中,用含m 的代数式表示这9个数的和为 9m .
8 9 10
14 15 16
20 21 22
表(1)
9m
8
9
10
14
16
20
21
22
a a+1 a+2
a+6 a+7 a+8
a+12 a+13 a+14
表(2)
m-7 m-6 m-5
m-1 m m+1
m+5 m+6 m+7
a+1
a+2
a+6
a+7
a+8
a+12
a+13
a+14
m-7
m-6
m-5
m-1
m+1
m+5
m+6
m+7
表(3)
4.将方框向右平移一列,则这9个数的和 增加9 ;将方框向下平移一列,则这9个数的和 增加54 .
归纳总结:探索规律列代数式时,先根据特例进行归纳、建立猜想,从而列出代数式.在探究过程中,感受由特殊到 一般 以及数形结合的思想.
增加9
增加54
一般
探索图形规律列代数式
完成课本本课时“大家谈谈”中的“方阵”问题,感受图形的规律探索,并完成下列各题.
1.课本“图3-2-3”是由点组成的n行n列的实心方阵,所以点的总数是 n2 个.
n2
2.课本“图3-2-4”是由每条边上的n个点组成的空心方阵,它可以看做n行n列的实心方阵减去 (n-2) 行 (n-2) 列的实心方阵所剩余的点所组成的,因此课本“图3-2-4”中点的总数是 n2-(n-2)2 个.当n=5时,方阵的总点数为 16 个.
(n-2)
(n-
2)
n2-(n-2)2
16
3.(1)观察课本“图3-2-5(1)”,共4条边,每条边上有 n 个点,共有 4n 个点,减去重复计算的 4 个点,方阵的总点数为 (4n-4) 个.当n=5时,方阵的总点数为 16 个.
(2)观察课本“图3-2-5(2)”,将点阵分成不重叠的 4 组,每组有 (n-1) 个点,方阵的总点数为 4(n-1) 个.当n=5时,方阵的总点数为 16 个.
n
4n
4
(4n-4)
16
4
(n-1)
4(n-1)
16
(3)观察课本“图3-2-5(3)”,将点阵分成不重叠的 4 组,其中上下两组各有 n 个点,另两组各有 (n-2) 个点,方阵的总点数为 [2n+2(n-2)] 个.当n=5时,方阵的总点数为 16 个.
4
n
(n-2)
[2n+2(n-2)]
16
思考:前面求得的四种不同的代数式都可以表示空心方阵的总点数吗?请任取一个n的值进行验证.
可以.(n的取值不唯一,但代入不同的式子结果都是一样的).例如:取n=6,所得结果都为20个.
归纳总结:找图形的规律,需要从图形的多少、大小、位置的变化等多角度观察分析.解决“方阵”问题,课本“图3-2-5(1)”用的是“包含-排除”法,(2)(3)用的是 分类 法.
分类
预习导学部分建议教师用15分钟左右的时间完成,通过两个知识点的学习,达成目标1和目标2的教学.因为这些题对学生来说有些难度,所以建议小组合作完成,再交流展示学习成果.
·导学建议·
摆火柴棒,探索图形规律列代数式
1.下面是同学们搭建的图形,我们一起进行探索吧.
(1)通过观察下图,可知第1个图中有4根火柴棒,第2个图中有7根火柴棒,第3个图中有 10 根火柴棒,第4个图中有 13 根火柴棒,第n个图中有 (3n+1) 根火柴棒.
10
13
(3n+1)
(2)用火柴棒按如图所示的方式搭图形,按照这样的规律搭下去,填写下表:
图形编号 ① ② ③ … n
火柴根数 7 12 17 … 5n+2
7
12
17
5n+2
(3)如图,按照这样的规律,摆第n个图需要火柴棒的数量为 (6n+2) 根.
(6n+2)
【方法归纳交流】第(1)题可以看作是先搭1根,然后再增加 3 根.第(2)题可以看作是先搭2根,然后再增加 5 根.第(3)题可以看作是先搭2根,然后再增加 6 根.总的来说就是从简单的图形入手,观察图形、数字、等式随着“序号”或“编号”增加时,后一个图形与前一个图形相比在数量上的变化情况,找出变化规律,从而推出一般性的结论.
3
5
6
教师也可用学生搭建的图形设计问题,或学生根据
自己搭建的图形自己设计问题请同桌解答,或事先将学生设计的不同图形拍摄成视频,课上进行研究.
·导学建议·
数线段条数,列代数式
2.在一条直线上有n个点,则以这些点中任意两点为端点的线段共有 条.
与数线段条数有关的推理思路:n个点中每个点与其他点组成 (n-1) 条线段,n个点共组成 n(n-1) 条线段,全部数重了,因此需 除以2 .
【变式拓展】在一条线段上取n个点,这n个点连同线段的两个端点一共有 (n+2) 个点,则以这些点中任意两点为端点的线段共有 (n+1)(n+2) 条.
(n-1)
n(n-1)
除以2
(n+2)
(n+1)(n+2)
探索数字规律列代数式
3.(1)有一列数5,15,25,35,…,则第9个数是 85 ,第n个数是 (10n-5) .
(2)观察,, ,,,…,则第n个数是( C )
A. B.
C. D.
85
(10n-5)
C
探索规律写出公式
4.观察下列等式:12+2×1=1×(1+2),22+2×2=2×(2+2),32+2×3=3×(3+2),…,则第n个等式可以表示为 n2+2n=n(n+2) .
【方法归纳交流】解答此类题目的一般方法是:从 特殊 情形入手,观察和分析所给等式左右两边的特点,然后归纳和总结出一般性的结论.
n2+2n=n(n+2)
特殊
合作探究建议用20分钟左右的时间完成,其中任务驱动一可让学生边拼图形边体会,任务驱动二可让学生举出几个特例数一数,任务驱动三、四可以提示学生观察序号与每个数字之间的关系,并在小组内交流合作.
·导学建议·
第三章 代数式
3.2 代数式 第4课时
1.会探索数学规律,列出代数式.
2.学会转化思想与化归思想.
◎重点:能探索发现数学规律并能正确验证.
◎难点:探索发现数学规律.
小小火柴棒能搭建很多美丽的图形,今天我们也来利用手中的火柴棒搭建一些常见图形,探索规律.例如,老师用火柴棒按如图所示的方式搭三角形.
照这样搭下去,则第n个图形要用 (2n+1) 根火柴棒.(用含n的代数式表示)
(2n+1)
你搭建的是什么图形呢?一会儿我们一起分享.
探索数字规律列代数式
完成课本本课时“一起探究”中的“数阵”问题,感受数字的规律探索,并完成下列各题.
1.找到数字15,并把它周围的8个数字填在表(1)中.
2.设方框左上角的数字为a,用含a的代数式表示其他8个数字并填在表(2)中,用含a的代数式表示这9个数的和为 9a+63 .
9a+
63
3.设方框正中间的数字为m,请用含m的代数式表示其他的8个数并填在表(3)中,用含m 的代数式表示这9个数的和为 9m .
8 9 10
14 15 16
20 21 22
表(1)
9m
8
9
10
14
16
20
21
22
a a+1 a+2
a+6 a+7 a+8
a+12 a+13 a+14
表(2)
m-7 m-6 m-5
m-1 m m+1
m+5 m+6 m+7
a+1
a+2
a+6
a+7
a+8
a+12
a+13
a+14
m-7
m-6
m-5
m-1
m+1
m+5
m+6
m+7
表(3)
4.将方框向右平移一列,则这9个数的和 增加9 ;将方框向下平移一列,则这9个数的和 增加54 .
归纳总结:探索规律列代数式时,先根据特例进行归纳、建立猜想,从而列出代数式.在探究过程中,感受由特殊到 一般 以及数形结合的思想.
增加9
增加54
一般
探索图形规律列代数式
完成课本本课时“大家谈谈”中的“方阵”问题,感受图形的规律探索,并完成下列各题.
1.课本“图3-2-3”是由点组成的n行n列的实心方阵,所以点的总数是 n2 个.
n2
2.课本“图3-2-4”是由每条边上的n个点组成的空心方阵,它可以看做n行n列的实心方阵减去 (n-2) 行 (n-2) 列的实心方阵所剩余的点所组成的,因此课本“图3-2-4”中点的总数是 n2-(n-2)2 个.当n=5时,方阵的总点数为 16 个.
(n-2)
(n-
2)
n2-(n-2)2
16
3.(1)观察课本“图3-2-5(1)”,共4条边,每条边上有 n 个点,共有 4n 个点,减去重复计算的 4 个点,方阵的总点数为 (4n-4) 个.当n=5时,方阵的总点数为 16 个.
(2)观察课本“图3-2-5(2)”,将点阵分成不重叠的 4 组,每组有 (n-1) 个点,方阵的总点数为 4(n-1) 个.当n=5时,方阵的总点数为 16 个.
n
4n
4
(4n-4)
16
4
(n-1)
4(n-1)
16
(3)观察课本“图3-2-5(3)”,将点阵分成不重叠的 4 组,其中上下两组各有 n 个点,另两组各有 (n-2) 个点,方阵的总点数为 [2n+2(n-2)] 个.当n=5时,方阵的总点数为 16 个.
4
n
(n-2)
[2n+2(n-2)]
16
思考:前面求得的四种不同的代数式都可以表示空心方阵的总点数吗?请任取一个n的值进行验证.
可以.(n的取值不唯一,但代入不同的式子结果都是一样的).例如:取n=6,所得结果都为20个.
归纳总结:找图形的规律,需要从图形的多少、大小、位置的变化等多角度观察分析.解决“方阵”问题,课本“图3-2-5(1)”用的是“包含-排除”法,(2)(3)用的是 分类 法.
分类
预习导学部分建议教师用15分钟左右的时间完成,通过两个知识点的学习,达成目标1和目标2的教学.因为这些题对学生来说有些难度,所以建议小组合作完成,再交流展示学习成果.
·导学建议·
摆火柴棒,探索图形规律列代数式
1.下面是同学们搭建的图形,我们一起进行探索吧.
(1)通过观察下图,可知第1个图中有4根火柴棒,第2个图中有7根火柴棒,第3个图中有 10 根火柴棒,第4个图中有 13 根火柴棒,第n个图中有 (3n+1) 根火柴棒.
10
13
(3n+1)
(2)用火柴棒按如图所示的方式搭图形,按照这样的规律搭下去,填写下表:
图形编号 ① ② ③ … n
火柴根数 7 12 17 … 5n+2
7
12
17
5n+2
(3)如图,按照这样的规律,摆第n个图需要火柴棒的数量为 (6n+2) 根.
(6n+2)
【方法归纳交流】第(1)题可以看作是先搭1根,然后再增加 3 根.第(2)题可以看作是先搭2根,然后再增加 5 根.第(3)题可以看作是先搭2根,然后再增加 6 根.总的来说就是从简单的图形入手,观察图形、数字、等式随着“序号”或“编号”增加时,后一个图形与前一个图形相比在数量上的变化情况,找出变化规律,从而推出一般性的结论.
3
5
6
教师也可用学生搭建的图形设计问题,或学生根据
自己搭建的图形自己设计问题请同桌解答,或事先将学生设计的不同图形拍摄成视频,课上进行研究.
·导学建议·
数线段条数,列代数式
2.在一条直线上有n个点,则以这些点中任意两点为端点的线段共有 条.
与数线段条数有关的推理思路:n个点中每个点与其他点组成 (n-1) 条线段,n个点共组成 n(n-1) 条线段,全部数重了,因此需 除以2 .
【变式拓展】在一条线段上取n个点,这n个点连同线段的两个端点一共有 (n+2) 个点,则以这些点中任意两点为端点的线段共有 (n+1)(n+2) 条.
(n-1)
n(n-1)
除以2
(n+2)
(n+1)(n+2)
探索数字规律列代数式
3.(1)有一列数5,15,25,35,…,则第9个数是 85 ,第n个数是 (10n-5) .
(2)观察,, ,,,…,则第n个数是( C )
A. B.
C. D.
85
(10n-5)
C
探索规律写出公式
4.观察下列等式:12+2×1=1×(1+2),22+2×2=2×(2+2),32+2×3=3×(3+2),…,则第n个等式可以表示为 n2+2n=n(n+2) .
【方法归纳交流】解答此类题目的一般方法是:从 特殊 情形入手,观察和分析所给等式左右两边的特点,然后归纳和总结出一般性的结论.
n2+2n=n(n+2)
特殊
合作探究建议用20分钟左右的时间完成,其中任务驱动一可让学生边拼图形边体会,任务驱动二可让学生举出几个特例数一数,任务驱动三、四可以提示学生观察序号与每个数字之间的关系,并在小组内交流合作.
·导学建议·
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
