河南省环际大联考“逐梦计划”2023-2024学年高二上学期12月阶段考试(三)数学试题(含答案)
文档属性
| 名称 | 河南省环际大联考“逐梦计划”2023-2024学年高二上学期12月阶段考试(三)数学试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 800.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-27 23:46:52 | ||
图片预览




文档简介
环际大联考
“逐梦计划”2023~2024学年度第一学期阶段考试(三)
高二数学试题
(试卷总分:150分 考试时间:120分钟)
注意事项:
1.答卷前,考生务必将自己的学校、班级、姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上。写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、单项选择题:本题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.直线的倾斜角为( )
A.0 B. C. D.不存在
2.已知双曲线的离心率为,则实数的值为( )
A. B. C.1 D.2
3.,,,,五人站成一排,如果,必须相邻,那么排法种数共有( )
A.24 B.120 C.48 D.60
4.已知点,,如果直线上有且只有一个点使得那么实数的值为( )
A.20 B. C. D.10
5.若直线过抛物线的焦点,与抛物线相交于,两点,且,则线段的中点到轴的距离为( )
A.6 B.8 C.10 D.12
6.已知直线与椭圆恒有公共点,则实数的取值范围为( )
A. B.或
C.且 D.且
7.如图,过抛物线的焦点的直线交抛物线于点,,交其准线于点,若,且,则此拋物线方程为( )
A. B. C. D.
8.在棱长为1的正方体中,、为线段上的两个三等分点,动点在内,且,则点的轨迹长度为( )
A. B. C. D.
二、多项选择题:本题共4小题,每小题5分,共20分,在每小题给出的四个选项中,有多个选项是符合题目要求的,全部选对得5分,部分选对得2分,有选错的得0分。
9.如图,在棱长为1的正方体中,为线段的中点,则下列说法正确的是( )
A.四面体的体积为
B.
C.向量在方向上的投影向量为
D.平面
10.已知曲线,则下列说法正确的是( )
A.若,则为椭圆
B.若,则为双曲线
C.若为椭圆,则其长轴长一定大于2
D.曲线不能表示圆
11.已知圆则下列说话正确的是( )
A.圆与直线必有两个交点
B.圆上存在4个点到直线的距离都等于1
C.圆与圆恰有三条公切线,则
D.动点在圆上,则
12.已知椭圆的左、右焦点分别为,,过的直线与交于,两点,若,则下列说话正确的是( )
A. B.的面积等于
C.直线的斜率为 D.的离心率等于
三、填空题:本题共4小题,每小题5分,共20分。
13.已知,则关于的方程有实数解的有序数对的个数为________.
14.已知直线过点,且,两点到直线的距离相等,则直线的方程为________.
15.如图,正方体的棱长为1,、分别为与的中点,则点到平面的距离为________.
16.已知抛物线的焦点为,准线为,若点在上,点在上,且是周长为12的正三角形.则抛物线的方程为________.
四、解答题:本大题共6小题,共70分.解答应写出必要的文字说明、证明过程或演算步骤。
17.(本题满分10分)已知的三个顶点分别为,,.
(1)求边上的中线所在直线的方程;
(2)求边上的高所在直线的方程.
18.(本题满分12分)已知直线与圆相交于,两点.
(1)求;
(2)若为圆上的动点,求的取值范围.
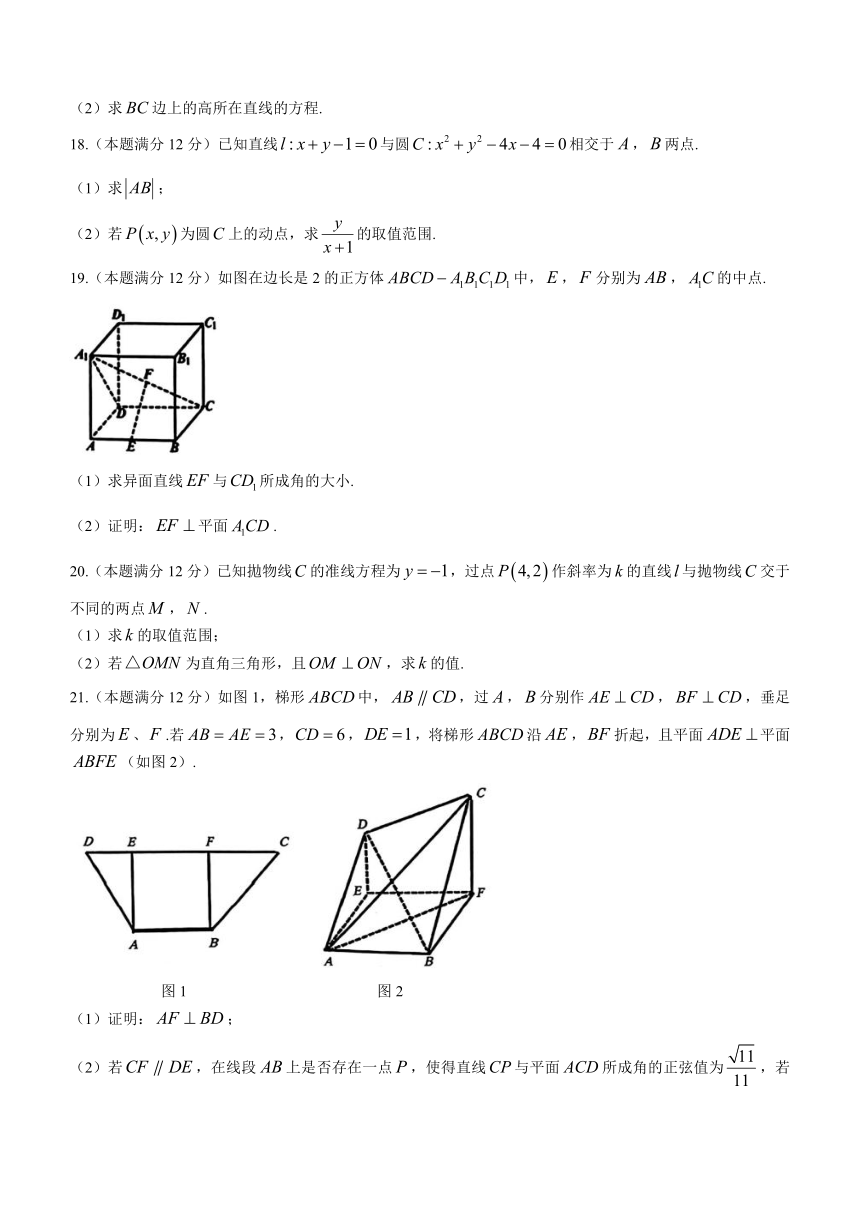
19.(本题满分12分)如图在边长是2的正方体中,,分别为,的中点.
(1)求异面直线与所成角的大小.
(2)证明:平面.
20.(本题满分12分)已知拋物线的准线方程为,过点作斜率为的直线与抛物线交于不同的两点,.
(1)求的取值范围;
(2)若为直角三角形,且,求的值.
21.(本题满分12分)如图1,梯形中,,过,分别作,,垂足分别为、.若,,,将梯形沿,折起,且平面平面(如图2).
图1 图2
(1)证明:;
(2)若,在线段上是否存在一点,使得直线与平面所成角的正弦值为,若存在,求出的长,若不存在,说明理由.
22.(本题满分12分)已知椭圆的离心率为,且椭圆过点.
(1)求的方程;
(2)设过点的动直线与相交于,两点,若为坐标原点,当面积最大时,求的方程.
环际大联考
“逐梦计划”2023~2024学年度第一学期阶段考试(三)
高二数学参考答案与评分标准
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1~4.CACD 5~8.ACBB
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多个选项是符合题目要求的,全部选对的得5分,部分选对的得2分,有选错的得0分.
9.ACD 10.BC 11.ABCD 12.AB
三、填空题:本题共4小题,每小题5分,共20分。
13.12
14.或
15.
16.
四、解答题:本大题共6小题,共70分。解答应写出必要的文字说明、证明过程或演算步骤。
17.解:(1)∵,,
∴的中点为.
又∵在边上的中线上,
∴所求直线方程为,
边上的中线所任直线的方程为.…………………………………………5分
(2)∵,,
∴直线的斜率为.而边上的高所住直线与直线垂直,
∴边上的高所在直线的斜率为.又∵任边上的高上,
∴所求直线方程为,
即边上的高所在组线的方程为.……………………………………10分
18.解:(1)∵圆
∴,………………………………………………………………………2分
∴圆心为,半径,
则圆心到直线的距离:,………………………………4分
∴.………………………………………………6分
(2)表示圆上的任意点与连线的斜率,
设,即,则直线与圆有公共点,
∴…………………………………………………………………………9分
∴
∴的取值范围为.…………………………………………………………12分
19.解:如图建系
,,,,,
∴,…………………………………………………………3分
(1)∴………………………………………………5分
∴
即异面直线与所成夹角为……………………………………………………7分
(2),
∴,……………………………………………………………………10分
∵,,且平面,
∴平面…………………………………………………………………………12分
法二:设平面的法向量为
,………………………………………………………………8分
∴,
令,则……………………………………………………………………10分
∴……………………………………………………………………………………11分
∴平面…………………………………………………………………………12分
20.解:(1)由题意,抛物线的方程为……………………………………2分
设直线方程为,
联立方程组,消去得,……………………4分
要使直线与抛物线交于不同的两点,,则,
即,
解得或,
综上,们取值范围为或.……………………………………6分
(2)设,,由(1)可知,是的两个根,
则,,………………………………………………7分
法一:因为为直像三作形,且,
所以,即,…………………………………………8分
国为
,……………………9分
所以有,
解得或,………………………………………………………………10分
当时,直线过原点,,,不能够构成三角形,
所以.…………………………………………………………………………12分
法二:因为为直角三角形,且,
所以,即,…………………………………………8分
因为,所以,
因为,所以,……………………………………………………10分
即,解得,
此时满足(1)中的取值范围,所以.…………………………………………12分
21.解:∵平面平而,平而,
平面平面,,
∴平面,……………………………………………………………………2分
(1)(法一)又平而,则.
又正方形中,,且,
平面,则平面,
又平面,则.……………………………………………………5分
(法二)∵平而,,
∴,,分别为,,轴建系
∴,,,,
∴,
∴
∴………………………………………………………………………5分
图2
(2)∵,∴平面,
∴∴,,
设平面的一个法向量为,
令,则………………………………………………………………8分
设在线段上存在一点且,
则,
设直线与平面所成的角为,
………………………………10分
则,不满足,所以不存在点满足题意.………………………………12分
22.解:(1)由已知
,解得
∴……………………………………………………………………5分
(2)由已知直线的斜率存在,设直线,,
∴联立方程可得:,整理后可得:
,
∵方程有两个不等实根
∴解得:或…………………………7分
又,
原点到直线的距离为
.……………………………………9分
∴
……………………………………………………………………10分
由均值不等式可得:
等号成立条件:
∴此时…………………………………………………………11分
∴的方程为或……………………………………12分
“逐梦计划”2023~2024学年度第一学期阶段考试(三)
高二数学试题
(试卷总分:150分 考试时间:120分钟)
注意事项:
1.答卷前,考生务必将自己的学校、班级、姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上。写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、单项选择题:本题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.直线的倾斜角为( )
A.0 B. C. D.不存在
2.已知双曲线的离心率为,则实数的值为( )
A. B. C.1 D.2
3.,,,,五人站成一排,如果,必须相邻,那么排法种数共有( )
A.24 B.120 C.48 D.60
4.已知点,,如果直线上有且只有一个点使得那么实数的值为( )
A.20 B. C. D.10
5.若直线过抛物线的焦点,与抛物线相交于,两点,且,则线段的中点到轴的距离为( )
A.6 B.8 C.10 D.12
6.已知直线与椭圆恒有公共点,则实数的取值范围为( )
A. B.或
C.且 D.且
7.如图,过抛物线的焦点的直线交抛物线于点,,交其准线于点,若,且,则此拋物线方程为( )
A. B. C. D.
8.在棱长为1的正方体中,、为线段上的两个三等分点,动点在内,且,则点的轨迹长度为( )
A. B. C. D.
二、多项选择题:本题共4小题,每小题5分,共20分,在每小题给出的四个选项中,有多个选项是符合题目要求的,全部选对得5分,部分选对得2分,有选错的得0分。
9.如图,在棱长为1的正方体中,为线段的中点,则下列说法正确的是( )
A.四面体的体积为
B.
C.向量在方向上的投影向量为
D.平面
10.已知曲线,则下列说法正确的是( )
A.若,则为椭圆
B.若,则为双曲线
C.若为椭圆,则其长轴长一定大于2
D.曲线不能表示圆
11.已知圆则下列说话正确的是( )
A.圆与直线必有两个交点
B.圆上存在4个点到直线的距离都等于1
C.圆与圆恰有三条公切线,则
D.动点在圆上,则
12.已知椭圆的左、右焦点分别为,,过的直线与交于,两点,若,则下列说话正确的是( )
A. B.的面积等于
C.直线的斜率为 D.的离心率等于
三、填空题:本题共4小题,每小题5分,共20分。
13.已知,则关于的方程有实数解的有序数对的个数为________.
14.已知直线过点,且,两点到直线的距离相等,则直线的方程为________.
15.如图,正方体的棱长为1,、分别为与的中点,则点到平面的距离为________.
16.已知抛物线的焦点为,准线为,若点在上,点在上,且是周长为12的正三角形.则抛物线的方程为________.
四、解答题:本大题共6小题,共70分.解答应写出必要的文字说明、证明过程或演算步骤。
17.(本题满分10分)已知的三个顶点分别为,,.
(1)求边上的中线所在直线的方程;
(2)求边上的高所在直线的方程.
18.(本题满分12分)已知直线与圆相交于,两点.
(1)求;
(2)若为圆上的动点,求的取值范围.
19.(本题满分12分)如图在边长是2的正方体中,,分别为,的中点.
(1)求异面直线与所成角的大小.
(2)证明:平面.
20.(本题满分12分)已知拋物线的准线方程为,过点作斜率为的直线与抛物线交于不同的两点,.
(1)求的取值范围;
(2)若为直角三角形,且,求的值.
21.(本题满分12分)如图1,梯形中,,过,分别作,,垂足分别为、.若,,,将梯形沿,折起,且平面平面(如图2).
图1 图2
(1)证明:;
(2)若,在线段上是否存在一点,使得直线与平面所成角的正弦值为,若存在,求出的长,若不存在,说明理由.
22.(本题满分12分)已知椭圆的离心率为,且椭圆过点.
(1)求的方程;
(2)设过点的动直线与相交于,两点,若为坐标原点,当面积最大时,求的方程.
环际大联考
“逐梦计划”2023~2024学年度第一学期阶段考试(三)
高二数学参考答案与评分标准
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1~4.CACD 5~8.ACBB
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多个选项是符合题目要求的,全部选对的得5分,部分选对的得2分,有选错的得0分.
9.ACD 10.BC 11.ABCD 12.AB
三、填空题:本题共4小题,每小题5分,共20分。
13.12
14.或
15.
16.
四、解答题:本大题共6小题,共70分。解答应写出必要的文字说明、证明过程或演算步骤。
17.解:(1)∵,,
∴的中点为.
又∵在边上的中线上,
∴所求直线方程为,
边上的中线所任直线的方程为.…………………………………………5分
(2)∵,,
∴直线的斜率为.而边上的高所住直线与直线垂直,
∴边上的高所在直线的斜率为.又∵任边上的高上,
∴所求直线方程为,
即边上的高所在组线的方程为.……………………………………10分
18.解:(1)∵圆
∴,………………………………………………………………………2分
∴圆心为,半径,
则圆心到直线的距离:,………………………………4分
∴.………………………………………………6分
(2)表示圆上的任意点与连线的斜率,
设,即,则直线与圆有公共点,
∴…………………………………………………………………………9分
∴
∴的取值范围为.…………………………………………………………12分
19.解:如图建系
,,,,,
∴,…………………………………………………………3分
(1)∴………………………………………………5分
∴
即异面直线与所成夹角为……………………………………………………7分
(2),
∴,……………………………………………………………………10分
∵,,且平面,
∴平面…………………………………………………………………………12分
法二:设平面的法向量为
,………………………………………………………………8分
∴,
令,则……………………………………………………………………10分
∴……………………………………………………………………………………11分
∴平面…………………………………………………………………………12分
20.解:(1)由题意,抛物线的方程为……………………………………2分
设直线方程为,
联立方程组,消去得,……………………4分
要使直线与抛物线交于不同的两点,,则,
即,
解得或,
综上,们取值范围为或.……………………………………6分
(2)设,,由(1)可知,是的两个根,
则,,………………………………………………7分
法一:因为为直像三作形,且,
所以,即,…………………………………………8分
国为
,……………………9分
所以有,
解得或,………………………………………………………………10分
当时,直线过原点,,,不能够构成三角形,
所以.…………………………………………………………………………12分
法二:因为为直角三角形,且,
所以,即,…………………………………………8分
因为,所以,
因为,所以,……………………………………………………10分
即,解得,
此时满足(1)中的取值范围,所以.…………………………………………12分
21.解:∵平面平而,平而,
平面平面,,
∴平面,……………………………………………………………………2分
(1)(法一)又平而,则.
又正方形中,,且,
平面,则平面,
又平面,则.……………………………………………………5分
(法二)∵平而,,
∴,,分别为,,轴建系
∴,,,,
∴,
∴
∴………………………………………………………………………5分
图2
(2)∵,∴平面,
∴∴,,
设平面的一个法向量为,
令,则………………………………………………………………8分
设在线段上存在一点且,
则,
设直线与平面所成的角为,
………………………………10分
则,不满足,所以不存在点满足题意.………………………………12分
22.解:(1)由已知
,解得
∴……………………………………………………………………5分
(2)由已知直线的斜率存在,设直线,,
∴联立方程可得:,整理后可得:
,
∵方程有两个不等实根
∴解得:或…………………………7分
又,
原点到直线的距离为
.……………………………………9分
∴
……………………………………………………………………10分
由均值不等式可得:
等号成立条件:
∴此时…………………………………………………………11分
∴的方程为或……………………………………12分
同课章节目录
