物理人教版(2019)必修第二册8.4机械能守恒定律(共24张ppt)
文档属性
| 名称 | 物理人教版(2019)必修第二册8.4机械能守恒定律(共24张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 12.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-12-28 13:10:40 | ||
图片预览







文档简介
(共24张PPT)
机械能守恒定律
必修第二册 第八章
分析和解决问题虽然会有各种各样具体的方法,但更宝贵的是领悟和掌握具有一定统帅作用的指导思想
重力势能
动能
相互转化
机械能
动能
弹性势能
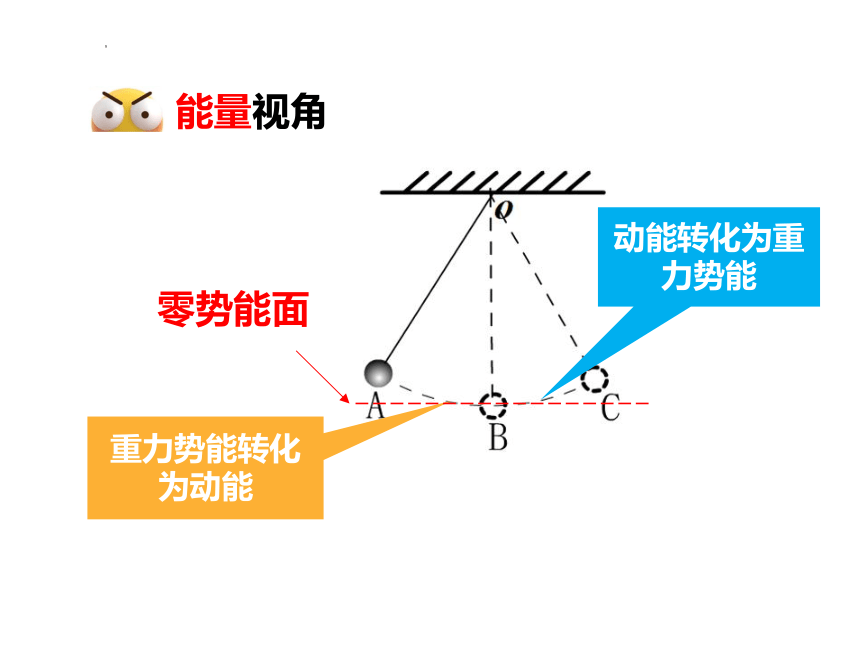
重力势能转化为动能
动能转化为重力势能
零势能面
能量视角
A
B
零势能面
A B C
重力势能
动能
机械能
mgh
0
mgh
0
0
EK
追寻守恒量
h
C
A
B
追寻守恒量
在势能、动能转化过程中,
可能存在守恒量!
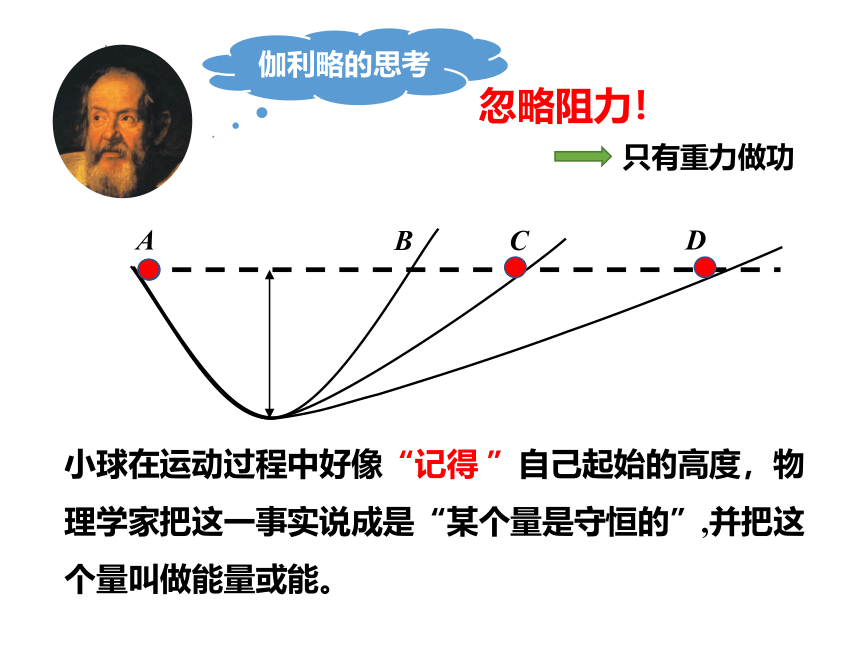
忽略阻力!
A
B
C
D
只有重力做功
伽利略的思考
小球在运动过程中好像“记得 ”自己起始的高度,物理学家把这一事实说成是“某个量是守恒的”,并把这个量叫做能量或能。
守恒:如果某一个物理量在某个过程中始终保持不变,那么我们就说这个物理量在此过程中守恒.
不变:如果一个物理量在两点的值一样(其它位置可能不同),那么我们就说这个物理量在这两点不变.
“守恒”和“不变”的区别
重力对物体做功
1
2
1-2:
机械能E1
做功视角
机械能E2
初态
末态
重力势能
减少量
动能
增加量
机械能E1
机械能E2
初态
末态
1
2
机械能守恒的条件
做功视角:
某个系统内除重力和弹力以外的其他力都不做功(或做功代数和为0)
能量视角:
只发生动能和势能(重力势能和弹性势能)的相互转化,没有机械能与其他能量的转化
动能
势能
机械能
只有重力或弹力做功的系统
的物体系统内,
,而总的 。
机械能守恒定律
(law of conservation of mechanical energy)
动能和势能可以相互转化
在只有重力或弹力做功
机械能保持不变
【典型示例1】判断下列各题中物体的机械能是否守恒?
小球从光滑弧形轨道上下滑
小球从粗糙弧形轨道上下滑
v
雨滴落体
小球倾斜(平)抛出(不计阻力)
m
v
【典型示例2】判断下列各题中物体的机械能是否守恒?
电梯匀速下降
火箭匀速升空
小球从光滑斜面下滑
θ
小球从A摆动到B的过程中(物体和弹簧组成的系统)
【例1】把一个小球用细绳悬挂起来,就成为一个摆。摆长为l,最大偏角为θ。小球运动到最低位置时的速度是多大?
解:拉力F不做功,只有重力G做功,小球机械能守恒。
以最低点为参考平面
G
FT
O
B
A
θ
l
【例2】用长为R 的非弹性轻绳将质量为m 的小球系住,并固定于垂直平面的O点,然后将球抬升到A点,保持绳子紧绷,且绳子和水平面夹角为θ=30°,然后将小球由静止释放。求小球落到最低点B点时的速度大小。(重力加速度为g,忽略空气阻力)
解:小球从静止释放到最低点B,重力势能转化为动能,机械能守恒,故:
对不对
θ
A
B
O
θ
A
B
O
θ
C
θ
在C点,绳子突然绷紧
绳子绷紧前后,机械能不守恒
在AC段中和BC段中机械能才守恒,球经过C点过程中,机械能损耗一部分转变成绳子内能
绳子的拉力对球做负功
绳子对球的拉力使得球沿绳子方向的速度快速变为零
θ
A
B
O
θ
C
θ
解:小球AC下落过程中,机械能守恒,故:
C点,沿绳方向速度由于绳子力的作用变为零
CB运动过程中,机械能守恒,故:
应用机械能守恒定律时,要注意适用条件!
vC
θ
θ
A
B
O
θ
C
vx
vy
一些有摩擦、有电场、物体间碰撞(弹性碰撞除外)等问题,机械能一般不守恒,除非题目中有特别说明或暗示。
守恒定律有一种奇妙的作用,它们能够透过纷乱芜杂的表面如此令人信服地指出一种潜藏在内部的守恒性,以至事件会立即从一团混沌变成井然有序的必然。
谢谢!
机械能守恒定律
必修第二册 第八章
分析和解决问题虽然会有各种各样具体的方法,但更宝贵的是领悟和掌握具有一定统帅作用的指导思想
重力势能
动能
相互转化
机械能
动能
弹性势能
重力势能转化为动能
动能转化为重力势能
零势能面
能量视角
A
B
零势能面
A B C
重力势能
动能
机械能
mgh
0
mgh
0
0
EK
追寻守恒量
h
C
A
B
追寻守恒量
在势能、动能转化过程中,
可能存在守恒量!
忽略阻力!
A
B
C
D
只有重力做功
伽利略的思考
小球在运动过程中好像“记得 ”自己起始的高度,物理学家把这一事实说成是“某个量是守恒的”,并把这个量叫做能量或能。
守恒:如果某一个物理量在某个过程中始终保持不变,那么我们就说这个物理量在此过程中守恒.
不变:如果一个物理量在两点的值一样(其它位置可能不同),那么我们就说这个物理量在这两点不变.
“守恒”和“不变”的区别
重力对物体做功
1
2
1-2:
机械能E1
做功视角
机械能E2
初态
末态
重力势能
减少量
动能
增加量
机械能E1
机械能E2
初态
末态
1
2
机械能守恒的条件
做功视角:
某个系统内除重力和弹力以外的其他力都不做功(或做功代数和为0)
能量视角:
只发生动能和势能(重力势能和弹性势能)的相互转化,没有机械能与其他能量的转化
动能
势能
机械能
只有重力或弹力做功的系统
的物体系统内,
,而总的 。
机械能守恒定律
(law of conservation of mechanical energy)
动能和势能可以相互转化
在只有重力或弹力做功
机械能保持不变
【典型示例1】判断下列各题中物体的机械能是否守恒?
小球从光滑弧形轨道上下滑
小球从粗糙弧形轨道上下滑
v
雨滴落体
小球倾斜(平)抛出(不计阻力)
m
v
【典型示例2】判断下列各题中物体的机械能是否守恒?
电梯匀速下降
火箭匀速升空
小球从光滑斜面下滑
θ
小球从A摆动到B的过程中(物体和弹簧组成的系统)
【例1】把一个小球用细绳悬挂起来,就成为一个摆。摆长为l,最大偏角为θ。小球运动到最低位置时的速度是多大?
解:拉力F不做功,只有重力G做功,小球机械能守恒。
以最低点为参考平面
G
FT
O
B
A
θ
l
【例2】用长为R 的非弹性轻绳将质量为m 的小球系住,并固定于垂直平面的O点,然后将球抬升到A点,保持绳子紧绷,且绳子和水平面夹角为θ=30°,然后将小球由静止释放。求小球落到最低点B点时的速度大小。(重力加速度为g,忽略空气阻力)
解:小球从静止释放到最低点B,重力势能转化为动能,机械能守恒,故:
对不对
θ
A
B
O
θ
A
B
O
θ
C
θ
在C点,绳子突然绷紧
绳子绷紧前后,机械能不守恒
在AC段中和BC段中机械能才守恒,球经过C点过程中,机械能损耗一部分转变成绳子内能
绳子的拉力对球做负功
绳子对球的拉力使得球沿绳子方向的速度快速变为零
θ
A
B
O
θ
C
θ
解:小球AC下落过程中,机械能守恒,故:
C点,沿绳方向速度由于绳子力的作用变为零
CB运动过程中,机械能守恒,故:
应用机械能守恒定律时,要注意适用条件!
vC
θ
θ
A
B
O
θ
C
vx
vy
一些有摩擦、有电场、物体间碰撞(弹性碰撞除外)等问题,机械能一般不守恒,除非题目中有特别说明或暗示。
守恒定律有一种奇妙的作用,它们能够透过纷乱芜杂的表面如此令人信服地指出一种潜藏在内部的守恒性,以至事件会立即从一团混沌变成井然有序的必然。
谢谢!
