4.3 第2课时 一元一次方程的应用(2)课件(共22张PPT) 苏科版七年级数学上册
文档属性
| 名称 | 4.3 第2课时 一元一次方程的应用(2)课件(共22张PPT) 苏科版七年级数学上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 726.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-28 00:00:00 | ||
图片预览








文档简介
(共22张PPT)
第4章 一元一次方程
4.3 用一元一次方程解决问题
第2课时 一元一次方程的应用(2)
1.会用表格分析实际问题中的数量关系;
2.能根据相等关系列一元一次方程解决问题.
◎重点:列一元一次方程解决实际问题.
◎难点:找出实际问题中的相等关系.
在一场篮球比赛中,小明投中的两分球、三分球共得28分,且他投中的两分球比三分球多4个,小明投中的两分球、三分球各几个?
用列表格的形式分析数量关系,列出方程解决问题
问题:北京冬奥会期间实行闭环管理,某大学冬奥志愿者分联络组和宣传组到奥运村开展工作.已知联络组有志愿者28人,宣传组有志愿者35人,由于工作需要,现从联络组调一部分志愿者到宣传组,使得宣传组人数是联络组人数的2倍,则需要从联络组调多少人到宣传组?
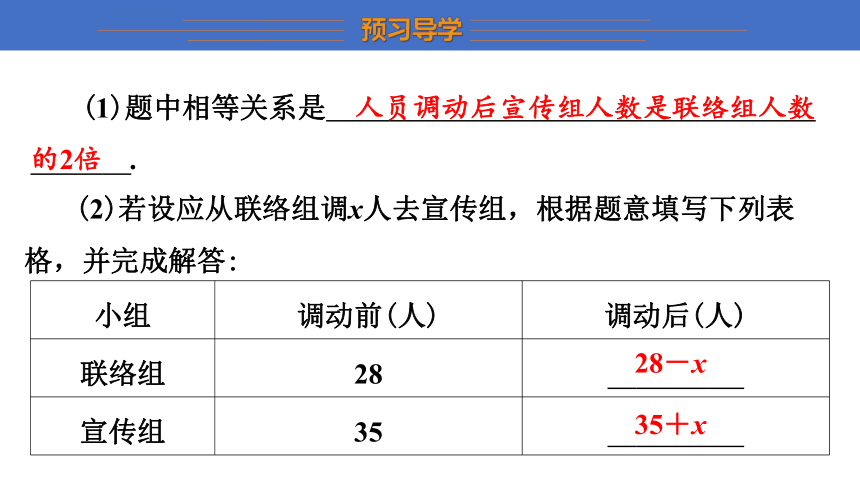
(1)题中相等关系是 人员调动后宣传组人数是联络组人数的2倍 .
(2)若设应从联络组调x人去宣传组,根据题意填写下列表格,并完成解答:
小组 调动前(人) 调动后(人)
联络组 28 28-x
宣传组 35 35+x
人员调动后宣传组人数是联络组人数
的2倍
28-x
35+x
解:设应从联络组调x人去宣传组,则宣传组人数为(35+x).
依题意得35+x=2(28-x),
解得x=7.
答:需要从联络组调7人到宣传组.
·导学建议·
当问题中的条件较多、数量关系较复杂时,可以通过列表格分析数量关系.首先设计表格,再将已知量填入表格,用所设未知数表示其余未知量并填入表格后,找出等量关系,列方程即可.
归纳总结 列表格时,通常可以先填写已知量,然后用未知数表示其余相关数量,并填写在表格相应位置,再根据数量之间相等关系列方程.
1.一个长方形的周长为26 cm,若这个长方形的长减少3 cm,就可成为一个正方形,设这个长方形的长为x cm,可列方程
( A )
A.x-3=13-x B.x+3=13-x
C.x+3=26-x D.x-3=26-x
A
2.一张试卷共有25道题,若做对1题得4分,做错1题扣1分,小明做了全部试题只得了70分,那么小明做对了( C )
A.17道 B.18道
C.19道 D.20道
C
3.某文艺团体组织了一场义演为“希望工程”募捐,共售出1000张门票.已知成人票每张8元,学生票每张5元,共得票款6950元,则成人票售出( C )
A.350张 B.500张
C.650张 D.700张
C
列一元一次方程解决调配问题
1.某车间有28名工人,生产某种螺栓和螺母,一个螺栓的两头各套上一个螺母,每人每天平均生产螺栓12个或螺母18个,问多少工人生产螺栓、多少工人生产螺母刚好使产品配套?(完成表格,并把此题解题过程补充完整)
品名 每人每天生产个数 工人数 总个数
螺栓 12 28-x 12(28-x)
螺母 18 x 18x
28-x
12(28-x)
18x
解:设有x名工人生产螺母.
由题意可知,18x=2×12(28-x),解得x=16.
答:16人生产螺母,12人生产螺栓.
问题中条件较多、数量关系较复杂时,注意引导学生利用表格分析问题中各数量之间的相互关系,方法:将已知、未知数量填入表格,理清关系,列方程.可以引导学生设不同的未知数,寻找不同的相等关系,列不同的方程.
方法归纳交流 先设计表格,再将已知、未知数量填入表格,利用表格中数据,找出问题中各数量之间的相互关系,列方程.
·导学建议·
列一元一次方程解决图表信息问题
2.一次联欢会上,甲、乙两班学生到集市上购买苹果,苹果的价格如下:
购买苹果数 不超过 10千克 超过10千克但 不超过20千克 超过20
千克
每千克价格 10元 9元 8元
甲班分两次共购买苹果30千克(第二次多于第一次),共付出256元;而乙班则一次性购买苹果30千克.
(1)乙班比甲班少付多少元?
(2)求甲班第一次购买苹果多少千克?
解:(1)256-8×30=256-240=16(元)
答:乙班比甲班少付16元.
(2)设甲班第一次购买了苹果x千克,则第二次购买了苹果(30-x)千克.
若第一次购买苹果不超过10千克,第二次购买苹果10千克以上,但不超过20千克,
10x+9(30-x)=256,
解得x=-14(舍弃),不符合题意.
若第一次购买苹果不超过10千克,第二次购买苹果20千克以上,
10x+8(30-x)=256,
解得x=8,
因为30-8=22>10,
所以符合题意.
若两次购买苹果都是10千克以上,但不超过20千克,
30×9=270>256,不符合题意.
答:甲班第一次购买了苹果8千克.
问题信息呈现在图表中,需要学生通过观察图示信息,结合文字,分析数据,从中获取相关信息,找出数量关系,建立方程模型解决问题.特别要注意表格行、列所表达的意义.
归纳总结 1.解答图文信息题的关键是读懂题意,能将“文字语言”转化为“符号语言”.
2.列方程解决问题,求出方程的解,应进一步考虑它是否符合问题的实际意义,解题时考虑问题要全面.
·导学建议·
1.足球比赛的计分规则:胜一场得3分,平一场得1分,负一场得0分.一个球队进行了14场比赛,共得19分,若这个队只负5场,那么这个队胜了( C )
A.3场 B.4场
C.5场 D.6场
C
2.某城市自来水收费实行阶梯水价,收费标准如下表所示:
月用水量 不超过10 m3的部分 超过10 m3不超过16 m3的部分 超过16 m3的部分
收费标准 (元/m3) 2.00 2.50 3.00
若某用户4月份交水费25元,则4月份所用水量是( B )
B
A.10 m3 B.12 m3
C.14 m3 D.16 m3
提示:设用水x m3,因为20<25<35,
所以该用户4月份用水超过了10 m3,未超过16 m3.
由题意得20+2.5(x-10)=25,
解得x=12,即用水12 m3.
故选B.
3.下面是某店的公告,会员购买一个夏威夷披萨的花费比公告前多7元,那么公告前一个夏威夷披萨的原价是( B )
A.45元 B.50元
C.55元 D.60元
B
第4章 一元一次方程
4.3 用一元一次方程解决问题
第2课时 一元一次方程的应用(2)
1.会用表格分析实际问题中的数量关系;
2.能根据相等关系列一元一次方程解决问题.
◎重点:列一元一次方程解决实际问题.
◎难点:找出实际问题中的相等关系.
在一场篮球比赛中,小明投中的两分球、三分球共得28分,且他投中的两分球比三分球多4个,小明投中的两分球、三分球各几个?
用列表格的形式分析数量关系,列出方程解决问题
问题:北京冬奥会期间实行闭环管理,某大学冬奥志愿者分联络组和宣传组到奥运村开展工作.已知联络组有志愿者28人,宣传组有志愿者35人,由于工作需要,现从联络组调一部分志愿者到宣传组,使得宣传组人数是联络组人数的2倍,则需要从联络组调多少人到宣传组?
(1)题中相等关系是 人员调动后宣传组人数是联络组人数的2倍 .
(2)若设应从联络组调x人去宣传组,根据题意填写下列表格,并完成解答:
小组 调动前(人) 调动后(人)
联络组 28 28-x
宣传组 35 35+x
人员调动后宣传组人数是联络组人数
的2倍
28-x
35+x
解:设应从联络组调x人去宣传组,则宣传组人数为(35+x).
依题意得35+x=2(28-x),
解得x=7.
答:需要从联络组调7人到宣传组.
·导学建议·
当问题中的条件较多、数量关系较复杂时,可以通过列表格分析数量关系.首先设计表格,再将已知量填入表格,用所设未知数表示其余未知量并填入表格后,找出等量关系,列方程即可.
归纳总结 列表格时,通常可以先填写已知量,然后用未知数表示其余相关数量,并填写在表格相应位置,再根据数量之间相等关系列方程.
1.一个长方形的周长为26 cm,若这个长方形的长减少3 cm,就可成为一个正方形,设这个长方形的长为x cm,可列方程
( A )
A.x-3=13-x B.x+3=13-x
C.x+3=26-x D.x-3=26-x
A
2.一张试卷共有25道题,若做对1题得4分,做错1题扣1分,小明做了全部试题只得了70分,那么小明做对了( C )
A.17道 B.18道
C.19道 D.20道
C
3.某文艺团体组织了一场义演为“希望工程”募捐,共售出1000张门票.已知成人票每张8元,学生票每张5元,共得票款6950元,则成人票售出( C )
A.350张 B.500张
C.650张 D.700张
C
列一元一次方程解决调配问题
1.某车间有28名工人,生产某种螺栓和螺母,一个螺栓的两头各套上一个螺母,每人每天平均生产螺栓12个或螺母18个,问多少工人生产螺栓、多少工人生产螺母刚好使产品配套?(完成表格,并把此题解题过程补充完整)
品名 每人每天生产个数 工人数 总个数
螺栓 12 28-x 12(28-x)
螺母 18 x 18x
28-x
12(28-x)
18x
解:设有x名工人生产螺母.
由题意可知,18x=2×12(28-x),解得x=16.
答:16人生产螺母,12人生产螺栓.
问题中条件较多、数量关系较复杂时,注意引导学生利用表格分析问题中各数量之间的相互关系,方法:将已知、未知数量填入表格,理清关系,列方程.可以引导学生设不同的未知数,寻找不同的相等关系,列不同的方程.
方法归纳交流 先设计表格,再将已知、未知数量填入表格,利用表格中数据,找出问题中各数量之间的相互关系,列方程.
·导学建议·
列一元一次方程解决图表信息问题
2.一次联欢会上,甲、乙两班学生到集市上购买苹果,苹果的价格如下:
购买苹果数 不超过 10千克 超过10千克但 不超过20千克 超过20
千克
每千克价格 10元 9元 8元
甲班分两次共购买苹果30千克(第二次多于第一次),共付出256元;而乙班则一次性购买苹果30千克.
(1)乙班比甲班少付多少元?
(2)求甲班第一次购买苹果多少千克?
解:(1)256-8×30=256-240=16(元)
答:乙班比甲班少付16元.
(2)设甲班第一次购买了苹果x千克,则第二次购买了苹果(30-x)千克.
若第一次购买苹果不超过10千克,第二次购买苹果10千克以上,但不超过20千克,
10x+9(30-x)=256,
解得x=-14(舍弃),不符合题意.
若第一次购买苹果不超过10千克,第二次购买苹果20千克以上,
10x+8(30-x)=256,
解得x=8,
因为30-8=22>10,
所以符合题意.
若两次购买苹果都是10千克以上,但不超过20千克,
30×9=270>256,不符合题意.
答:甲班第一次购买了苹果8千克.
问题信息呈现在图表中,需要学生通过观察图示信息,结合文字,分析数据,从中获取相关信息,找出数量关系,建立方程模型解决问题.特别要注意表格行、列所表达的意义.
归纳总结 1.解答图文信息题的关键是读懂题意,能将“文字语言”转化为“符号语言”.
2.列方程解决问题,求出方程的解,应进一步考虑它是否符合问题的实际意义,解题时考虑问题要全面.
·导学建议·
1.足球比赛的计分规则:胜一场得3分,平一场得1分,负一场得0分.一个球队进行了14场比赛,共得19分,若这个队只负5场,那么这个队胜了( C )
A.3场 B.4场
C.5场 D.6场
C
2.某城市自来水收费实行阶梯水价,收费标准如下表所示:
月用水量 不超过10 m3的部分 超过10 m3不超过16 m3的部分 超过16 m3的部分
收费标准 (元/m3) 2.00 2.50 3.00
若某用户4月份交水费25元,则4月份所用水量是( B )
B
A.10 m3 B.12 m3
C.14 m3 D.16 m3
提示:设用水x m3,因为20<25<35,
所以该用户4月份用水超过了10 m3,未超过16 m3.
由题意得20+2.5(x-10)=25,
解得x=12,即用水12 m3.
故选B.
3.下面是某店的公告,会员购买一个夏威夷披萨的花费比公告前多7元,那么公告前一个夏威夷披萨的原价是( B )
A.45元 B.50元
C.55元 D.60元
B
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
