3.3 代数式的值(第2课时) 课件 44张PPT 冀教版七年级数学上册
文档属性
| 名称 | 3.3 代数式的值(第2课时) 课件 44张PPT 冀教版七年级数学上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 881.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-28 00:00:00 | ||
图片预览











文档简介
(共44张PPT)
第三章 代数式
3.3 代数式的值 第2课时
1.能够根据具体情境列出代数式,再求代数式的值.
2.体会由特殊到一般再到特殊的建立数学模型和求解的过程.
◎重点:能够根据具体情境列出代数式,再求代数式的值.
◎难点:理解两个数量的对应关系.
营养学家用身体质量指数来判断人体的健康状况,这个指数等于人体质量m(千克)除以人体身高h(米)的平方所得的商.一个健康的人的身体质量指数P在20~25之间;身体质量指数P低于18,属于不健康的瘦;身体质量指数P高于30,属于不健康的胖.请先用含有m,h的代数式表示身体质量指数P,然后测量一下你的身高和体重,判断一下你健康吗?
答案:P=.
实际问题中两个变量之间的关系
1.完成课本本课时“做一做”, 体会列代数式及求代数式的值在生活中的作用,并完成下面的填空题.
(1)小亮离开家的路程s1= 80t ,小亮距学校的路程s2= 1280-80t .
80t
1280-80t
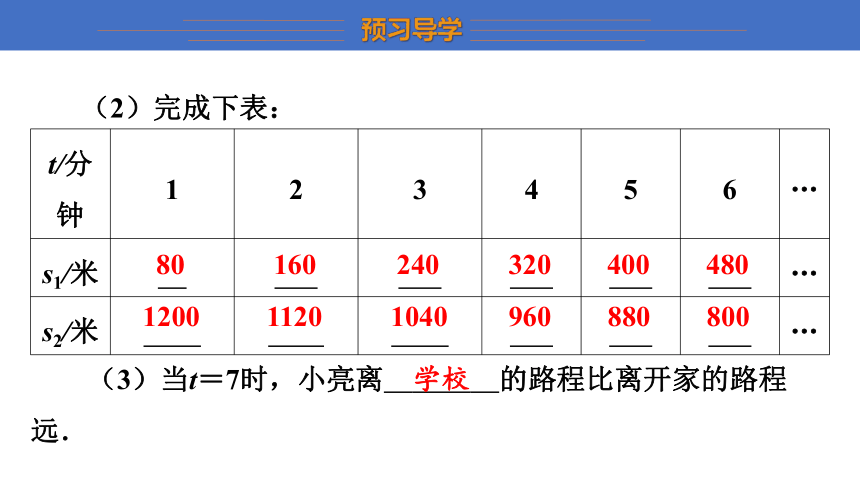
(2)完成下表:
t/分钟 1 2 3 4 5 6 …
s1/米 80 160 240 320 400 480 …
s2/米 1200 1120 1040 960 880 800 …
80
160
240
320
400
480
1200
1120
1040
960
880
800
(3)当t=7时,小亮离 学校 的路程比离开家的路程远.
学校
思考:(1)当t=16时,小亮在哪?t可以取17吗?
(2)怎样用含t的等量关系表示小亮离开家的路程和距学校的路程一样?
(1)在学校,不可以取17.(2)80t=1280-80t.
2.完成课本本课时“一起探究”,体会由特殊到一般再到特殊的建立数学模型和求解的过程,并完成下面的填空题.
思考:确定耕地面积与耗油量之间的关系的关键是什么?
确定耕地1公顷的耗油量.
(1)算出几组具体数值:观察油量表可得,当a=0.4公顷时,b= 10 升;当a=0.6公顷时,b= 15 升;当a=1公顷时,b= 25 升.
10
15
25
(2)发现规律:由表格可知,每耕1公顷地,耗油量为 25 升.
(3)列出代数式:耗油量b(升)与耕地面积a(公顷)之间的关系为 b=25a .
25
b=25a
(4)应用:①当a=0.5公顷时,b= 12.5 升;当a=2公顷时,b= 50 升.
②当b=12升时,a= 公顷;当b=40升时,a= 公顷.
12.5
50
归纳总结:通过观察几组具体值,发现两个数量之间呈现的规律并用代数式表示出来,然后通过求 代数式 的值解决更多具体的问题,这是解决数量关系问题的通法.这种“由特殊到一般再到特殊”的分析方法是建立数学模型和求解的一般过程.
代数式
数量x与数量y之间的对应关系如下表所示:
x 0 2 4 6 8 …
y 15 20 25 30 35 …
(1)由表格直接写出y与x之间的关系式.
(2)当x=20时,y的值是多少?
解:(1)y=15+x.(2)65.
·导学建议·
预习导学部分建议教师用15分钟左右的时间完成,通过该知识点的学习,达成目标1和目标2的教学.自学时,教师重点关注学生对两个思考题的完成情况.
代数式帮你解决工程问题
1.某企业生产一批电视机,每天生产m台,计划生产a天.为适应市场需求,需要提前3天完成,用代数式表示出实际每天要多生产多少台电视机?并求出当m=100,a=28时,每天多生产的电视机的台数.
为顺利解决这道题,可以先完成下面的表格:
这批电视机的总台数 ma
实际生产的天数 a-3
实际每天生产的台数
实际每天多生产的台数 -m
ma
a-3
-m
解:实际每天多生产台.当m=100,a=28时, -m=-100=12(台),所以实际每天多生产12台.
解:实际每天多生产台.当m=100,a=28时,
-m=-100=12(台),所以实际每天多生产12
台.
【方法归纳交流】对于实际问题,要仔细看清题意,理解每个数量表达的意思.为了表示清楚,可以列出 表格 帮助列代数式,通过一步步列表,问题会轻松解决.
表格
代数式帮你节水
2.我国是一个严重缺水的国家,大家都应该加倍珍惜水资源,节约用水.据测试:拧不紧的水龙头每分钟滴出100滴水,每滴水约0.05毫升.小康同学洗手后,没有把水龙头拧紧,水龙头以测试的速度滴水,当小康离开x分钟后,水龙头滴出y毫升的水.
(2)当小康离开10分钟后,水龙头滴水多少毫升?
解:(1)y=5x.
(1)用含x的代数式表示y.
(2)50毫升.
代数式帮你做决策
3.某种铂金饰品在甲、乙两个商店销售.甲店标价477元/克,按标价出售,不优惠.乙店标价530元/克,但若买的铂金饰品重量超过3克,则超出部分可打八折出售.
(2)李阿姨要买一条重量为5克的此种铂金饰品,到哪个商店购买更合算?
解:(1)y甲=477x,y乙=530×3+530(x-3)·80%.
(2)当x=5时,y甲=2385,y乙=2438.所以买5克时,到甲商店购买更合算.
(1)分别写出到甲、乙商店购买该种铂金饰品所需费用y(元)和重量x(克)(x大于3)之间的关系式.
【变式拓展】某风景区集体门票收费标准如下:20人以内(含20人)每人25元;超过20人时,超过的部分每人10元.
(1)写出应收门票费y(元)与游览人数x(人)之间的关系式.
(2)某班54名学生去该风景区游览时,购买门票共花多少元?
解:(1)当人数在20以内(含20人)时,y=25x;
超过20人时,y=20×25+10(x-20)=500+10(x-20).
(2)54名超过了20,将x=54代入y=500+10(x-20),得y=840.所以54名学生购买门票共花840元.
【方法归纳交流】当已知量是用字母表示数的形式给出的,且字母的取值不同还会影响问题的解决时,就需要我们按不同情况分类,然后再逐一研究解决,这种数学思想就是 分类讨论 思想.
分类讨
论
建立数学模型解决问题
4.用同样大小的黑色棋子按如图所示的规律摆放:
(1)第5个图形中有多少颗黑色棋子?
(2)若设第n个图形中黑色棋子有m颗,请直接写出m与n 的关系式.
(3)第671个图形中有多少颗黑色棋子?
解:(1)18.(2)m=3(n+1).(3)当n=671时,m=3(n+1)=2016,所以第671个图形中有2016颗黑色棋子.
【变式演练】一种长方形餐桌的四周可供6人用餐,现把若干张这样的餐桌按如图所示的方式进行拼接.
(1)若2张这样的餐桌拼接起来,则四周可坐多少人?若3张这样的餐桌拼接起来,则四周可坐多少人?
解:(1)10人,14人.
(2)若n张这样的餐桌拼接起来,四周可坐y人,请用含n的代数式表示y.
(3)若8张这样的餐桌拼接起来,则四周可坐多少人?
(2)y=4n+2.
(3)当n=8时,y=4×8+2=34人.
一、作业目标
1.理解列代数式的规则,利用数量关系列出正确的代数式,培养抽象思维能力.
2.利用列代数式知识解决规律型问题,感受数形结合的数学思想.
《代数式》实践作业
二、作业内容
1下列代数式中,书写不规范的是( D )
A.a3 B.3x+1 C. D.1×m
D
2代数式a2-的正确解释是( A )
A.a的平方与b的倒数的差
B.a与b的倒数的差的平方
C.a的平方与b的差的倒数
D.a与b的差的平方的倒数
A
3如图,按此规律,第6行最后一个数字是 16 ,第 674 行最后一个数是2020.
1
2 3 4
3 4 5
6 7
4 5 6
7 8 9 10
16
674
……
4观察下列一组图形中点的个数,其中第1个图中共有4个点,第2个图中共有10个点,第3个图中共有19个点,…,按此规律第6个图中共有点的个数是 64 .
64
5小明在他家的时钟(如图)上安装了一个电脑软件,他设定当钟声在n点钟响起后,下次则在(3n-1)h后响起,例如钟声第1次在3点钟响起,那么第2次在3×3-1=8(h)后,即11点响起;第3次在3×11-1=32(h)后,即7点响起,以此类推,…,现在第1次钟声响起时为2点钟,那么第3次响起时为 3 点,第2022次响起时为 3 点.
3
3
6将一列有理数-1,2,-3,4,-5,6,…,按如图的方式有序排列,4所在位置为峰1,-9所在位置为峰2,….
(1)处在峰5位置的有理数是 24 ;
(2)2022应排在A,B,C,D,E中 A 的位置上.
24
A
7请根据图示的对话解答下列问题.
(1)求:a,b,c的值.
(2)计算7-a+3b-c值.
解:(1)∵a的相反数是-3,b的绝对值是6,
∴a=3,b=±6.
∵a>b,
∴b=-6.
∵b与c的和是-9,
∴c=-9-(-6)=-9+6=-3.
(2)当a=3,b=-6,c=-3时,
7-a+3b-c=7-3+3×(-6)-(-3)
=7-3+(-18)+3
=-11.
8如图,一个长方形运动场被分隔成A,B,A,B,C共5个区,A区是边长为a m的正方形,C区是边长为c m的正方形.
(1)列式表示每个B区长方形场地的周长,并将式子化简;
(2)列式表示整个长方形运动场的周长,并将式子化简;
(3)如果a=40,c=10,求整个长方形运动场的面积.
解:(1)2[(a+c)+(a-c)]=2(a+c+a-c)=4a(m).
(2)2[(a+a+c)+(a+a-c)]=2(a+a+c+a+a-c)=8a(m).
(3)当a=40,c=10时,
长=2a+c=90(m),宽=2a-c=70(m),
所以面积=90×70=6300(m2).
9某县防疫部门配送新冠疫情物资,甲、乙两仓库分别有防疫物资30箱和50箱,A、B两地分别需要防疫物资20箱和60箱.已知从甲、乙两仓库到A、B两地的运价如表:
到A地 到B地
甲仓库 每箱15元 每箱12元
乙仓库 每箱10元 每箱9元
(1)若从甲仓库运到A地的防疫物资为x箱,则用含x的代数式表示从甲仓库运到B地的防疫物资为 箱,从乙仓库将防疫物资运到B地的运输费用为 元;
(2)求把全部防疫物资从甲、乙两仓库运到A、B两地的总运输费(用含x的代数式表示并化简);
(3)如果从甲仓库运到A地的防疫物资为10箱,那么总运输费为多少元?
(1)∵甲仓库有防疫物资30箱,从甲仓库运到A地的防疫物资为x箱,
∴从甲仓库运到B地的防疫物资为(30-x)箱.
∵B地需要防疫物资60箱,从甲仓库运到B地的防疫物资为(30-x)箱,
∴从乙仓库运到B地的防疫物资为60-30+x=(30+x)箱,
∴从乙仓库将防疫物资运到B地的运输费用为9×(30+x)=(270+9x)元.
故答案为(30-x),(270+9x).
(2)总运费:15x+12(30-x)+10(20-x)+9(30+x)=(2x+830)元,
∴全部防疫物资从甲、乙两仓库运到A、B两地的总运输费为(2x+830)元.
(3)当x=10时,2x+830=2×10+830=850,
∴总运输费为850元.
第三章 代数式
3.3 代数式的值 第2课时
1.能够根据具体情境列出代数式,再求代数式的值.
2.体会由特殊到一般再到特殊的建立数学模型和求解的过程.
◎重点:能够根据具体情境列出代数式,再求代数式的值.
◎难点:理解两个数量的对应关系.
营养学家用身体质量指数来判断人体的健康状况,这个指数等于人体质量m(千克)除以人体身高h(米)的平方所得的商.一个健康的人的身体质量指数P在20~25之间;身体质量指数P低于18,属于不健康的瘦;身体质量指数P高于30,属于不健康的胖.请先用含有m,h的代数式表示身体质量指数P,然后测量一下你的身高和体重,判断一下你健康吗?
答案:P=.
实际问题中两个变量之间的关系
1.完成课本本课时“做一做”, 体会列代数式及求代数式的值在生活中的作用,并完成下面的填空题.
(1)小亮离开家的路程s1= 80t ,小亮距学校的路程s2= 1280-80t .
80t
1280-80t
(2)完成下表:
t/分钟 1 2 3 4 5 6 …
s1/米 80 160 240 320 400 480 …
s2/米 1200 1120 1040 960 880 800 …
80
160
240
320
400
480
1200
1120
1040
960
880
800
(3)当t=7时,小亮离 学校 的路程比离开家的路程远.
学校
思考:(1)当t=16时,小亮在哪?t可以取17吗?
(2)怎样用含t的等量关系表示小亮离开家的路程和距学校的路程一样?
(1)在学校,不可以取17.(2)80t=1280-80t.
2.完成课本本课时“一起探究”,体会由特殊到一般再到特殊的建立数学模型和求解的过程,并完成下面的填空题.
思考:确定耕地面积与耗油量之间的关系的关键是什么?
确定耕地1公顷的耗油量.
(1)算出几组具体数值:观察油量表可得,当a=0.4公顷时,b= 10 升;当a=0.6公顷时,b= 15 升;当a=1公顷时,b= 25 升.
10
15
25
(2)发现规律:由表格可知,每耕1公顷地,耗油量为 25 升.
(3)列出代数式:耗油量b(升)与耕地面积a(公顷)之间的关系为 b=25a .
25
b=25a
(4)应用:①当a=0.5公顷时,b= 12.5 升;当a=2公顷时,b= 50 升.
②当b=12升时,a= 公顷;当b=40升时,a= 公顷.
12.5
50
归纳总结:通过观察几组具体值,发现两个数量之间呈现的规律并用代数式表示出来,然后通过求 代数式 的值解决更多具体的问题,这是解决数量关系问题的通法.这种“由特殊到一般再到特殊”的分析方法是建立数学模型和求解的一般过程.
代数式
数量x与数量y之间的对应关系如下表所示:
x 0 2 4 6 8 …
y 15 20 25 30 35 …
(1)由表格直接写出y与x之间的关系式.
(2)当x=20时,y的值是多少?
解:(1)y=15+x.(2)65.
·导学建议·
预习导学部分建议教师用15分钟左右的时间完成,通过该知识点的学习,达成目标1和目标2的教学.自学时,教师重点关注学生对两个思考题的完成情况.
代数式帮你解决工程问题
1.某企业生产一批电视机,每天生产m台,计划生产a天.为适应市场需求,需要提前3天完成,用代数式表示出实际每天要多生产多少台电视机?并求出当m=100,a=28时,每天多生产的电视机的台数.
为顺利解决这道题,可以先完成下面的表格:
这批电视机的总台数 ma
实际生产的天数 a-3
实际每天生产的台数
实际每天多生产的台数 -m
ma
a-3
-m
解:实际每天多生产台.当m=100,a=28时, -m=-100=12(台),所以实际每天多生产12台.
解:实际每天多生产台.当m=100,a=28时,
-m=-100=12(台),所以实际每天多生产12
台.
【方法归纳交流】对于实际问题,要仔细看清题意,理解每个数量表达的意思.为了表示清楚,可以列出 表格 帮助列代数式,通过一步步列表,问题会轻松解决.
表格
代数式帮你节水
2.我国是一个严重缺水的国家,大家都应该加倍珍惜水资源,节约用水.据测试:拧不紧的水龙头每分钟滴出100滴水,每滴水约0.05毫升.小康同学洗手后,没有把水龙头拧紧,水龙头以测试的速度滴水,当小康离开x分钟后,水龙头滴出y毫升的水.
(2)当小康离开10分钟后,水龙头滴水多少毫升?
解:(1)y=5x.
(1)用含x的代数式表示y.
(2)50毫升.
代数式帮你做决策
3.某种铂金饰品在甲、乙两个商店销售.甲店标价477元/克,按标价出售,不优惠.乙店标价530元/克,但若买的铂金饰品重量超过3克,则超出部分可打八折出售.
(2)李阿姨要买一条重量为5克的此种铂金饰品,到哪个商店购买更合算?
解:(1)y甲=477x,y乙=530×3+530(x-3)·80%.
(2)当x=5时,y甲=2385,y乙=2438.所以买5克时,到甲商店购买更合算.
(1)分别写出到甲、乙商店购买该种铂金饰品所需费用y(元)和重量x(克)(x大于3)之间的关系式.
【变式拓展】某风景区集体门票收费标准如下:20人以内(含20人)每人25元;超过20人时,超过的部分每人10元.
(1)写出应收门票费y(元)与游览人数x(人)之间的关系式.
(2)某班54名学生去该风景区游览时,购买门票共花多少元?
解:(1)当人数在20以内(含20人)时,y=25x;
超过20人时,y=20×25+10(x-20)=500+10(x-20).
(2)54名超过了20,将x=54代入y=500+10(x-20),得y=840.所以54名学生购买门票共花840元.
【方法归纳交流】当已知量是用字母表示数的形式给出的,且字母的取值不同还会影响问题的解决时,就需要我们按不同情况分类,然后再逐一研究解决,这种数学思想就是 分类讨论 思想.
分类讨
论
建立数学模型解决问题
4.用同样大小的黑色棋子按如图所示的规律摆放:
(1)第5个图形中有多少颗黑色棋子?
(2)若设第n个图形中黑色棋子有m颗,请直接写出m与n 的关系式.
(3)第671个图形中有多少颗黑色棋子?
解:(1)18.(2)m=3(n+1).(3)当n=671时,m=3(n+1)=2016,所以第671个图形中有2016颗黑色棋子.
【变式演练】一种长方形餐桌的四周可供6人用餐,现把若干张这样的餐桌按如图所示的方式进行拼接.
(1)若2张这样的餐桌拼接起来,则四周可坐多少人?若3张这样的餐桌拼接起来,则四周可坐多少人?
解:(1)10人,14人.
(2)若n张这样的餐桌拼接起来,四周可坐y人,请用含n的代数式表示y.
(3)若8张这样的餐桌拼接起来,则四周可坐多少人?
(2)y=4n+2.
(3)当n=8时,y=4×8+2=34人.
一、作业目标
1.理解列代数式的规则,利用数量关系列出正确的代数式,培养抽象思维能力.
2.利用列代数式知识解决规律型问题,感受数形结合的数学思想.
《代数式》实践作业
二、作业内容
1下列代数式中,书写不规范的是( D )
A.a3 B.3x+1 C. D.1×m
D
2代数式a2-的正确解释是( A )
A.a的平方与b的倒数的差
B.a与b的倒数的差的平方
C.a的平方与b的差的倒数
D.a与b的差的平方的倒数
A
3如图,按此规律,第6行最后一个数字是 16 ,第 674 行最后一个数是2020.
1
2 3 4
3 4 5
6 7
4 5 6
7 8 9 10
16
674
……
4观察下列一组图形中点的个数,其中第1个图中共有4个点,第2个图中共有10个点,第3个图中共有19个点,…,按此规律第6个图中共有点的个数是 64 .
64
5小明在他家的时钟(如图)上安装了一个电脑软件,他设定当钟声在n点钟响起后,下次则在(3n-1)h后响起,例如钟声第1次在3点钟响起,那么第2次在3×3-1=8(h)后,即11点响起;第3次在3×11-1=32(h)后,即7点响起,以此类推,…,现在第1次钟声响起时为2点钟,那么第3次响起时为 3 点,第2022次响起时为 3 点.
3
3
6将一列有理数-1,2,-3,4,-5,6,…,按如图的方式有序排列,4所在位置为峰1,-9所在位置为峰2,….
(1)处在峰5位置的有理数是 24 ;
(2)2022应排在A,B,C,D,E中 A 的位置上.
24
A
7请根据图示的对话解答下列问题.
(1)求:a,b,c的值.
(2)计算7-a+3b-c值.
解:(1)∵a的相反数是-3,b的绝对值是6,
∴a=3,b=±6.
∵a>b,
∴b=-6.
∵b与c的和是-9,
∴c=-9-(-6)=-9+6=-3.
(2)当a=3,b=-6,c=-3时,
7-a+3b-c=7-3+3×(-6)-(-3)
=7-3+(-18)+3
=-11.
8如图,一个长方形运动场被分隔成A,B,A,B,C共5个区,A区是边长为a m的正方形,C区是边长为c m的正方形.
(1)列式表示每个B区长方形场地的周长,并将式子化简;
(2)列式表示整个长方形运动场的周长,并将式子化简;
(3)如果a=40,c=10,求整个长方形运动场的面积.
解:(1)2[(a+c)+(a-c)]=2(a+c+a-c)=4a(m).
(2)2[(a+a+c)+(a+a-c)]=2(a+a+c+a+a-c)=8a(m).
(3)当a=40,c=10时,
长=2a+c=90(m),宽=2a-c=70(m),
所以面积=90×70=6300(m2).
9某县防疫部门配送新冠疫情物资,甲、乙两仓库分别有防疫物资30箱和50箱,A、B两地分别需要防疫物资20箱和60箱.已知从甲、乙两仓库到A、B两地的运价如表:
到A地 到B地
甲仓库 每箱15元 每箱12元
乙仓库 每箱10元 每箱9元
(1)若从甲仓库运到A地的防疫物资为x箱,则用含x的代数式表示从甲仓库运到B地的防疫物资为 箱,从乙仓库将防疫物资运到B地的运输费用为 元;
(2)求把全部防疫物资从甲、乙两仓库运到A、B两地的总运输费(用含x的代数式表示并化简);
(3)如果从甲仓库运到A地的防疫物资为10箱,那么总运输费为多少元?
(1)∵甲仓库有防疫物资30箱,从甲仓库运到A地的防疫物资为x箱,
∴从甲仓库运到B地的防疫物资为(30-x)箱.
∵B地需要防疫物资60箱,从甲仓库运到B地的防疫物资为(30-x)箱,
∴从乙仓库运到B地的防疫物资为60-30+x=(30+x)箱,
∴从乙仓库将防疫物资运到B地的运输费用为9×(30+x)=(270+9x)元.
故答案为(30-x),(270+9x).
(2)总运费:15x+12(30-x)+10(20-x)+9(30+x)=(2x+830)元,
∴全部防疫物资从甲、乙两仓库运到A、B两地的总运输费为(2x+830)元.
(3)当x=10时,2x+830=2×10+830=850,
∴总运输费为850元.
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
