1.10 有理数的乘方课件 22张PPT 冀教版数学七年级上册
文档属性
| 名称 | 1.10 有理数的乘方课件 22张PPT 冀教版数学七年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 768.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-28 15:25:43 | ||
图片预览








文档简介
(共22张PPT)
第一章 有理数
1.10 有理数的乘方
1.明白乘方的意义,会进行有理数的乘方运算.
2.经历探索幂的符号法则的过程,会判断幂的符号.
◎重点:乘方的意义,幂的符号法则.
◎难点:有理数的乘方运算.
·导学建议·
有理数乘方的意义内容比较简单,可以让学生先自学再讲解,要求:讲清楚乘方、幂、底数、指数的概念及它们之间的关系.
怎样计算边长为5 cm的正方形的面积?怎样计算棱长为3 cm的正方体的体积?
有理数的乘方
1.完成课本“试着做做”.
(1)53,34;(2)(-4)4,3.
2.阅读课本“试着做做”后面的内容,解决下列问题.
(1)求 n个相同因数的积 的运算叫做乘方.例如:= an .
(2)乘方的结果叫做 幂 .在an中,a叫做 底数 ,n叫做 指数 .
(3)an读作什么?与同桌读一读“试着做做”中的幂.
a的n次幂或a的n次方;略.
n个相同因数的积
an
幂
底数
指数
(4)举例说明怎样表示一个数的一次方?
5的一次方可表示为51,通常1省略不写.
·导学建议·
教师要强调指数为1时通常省略不写,但不要误认为指数为0.
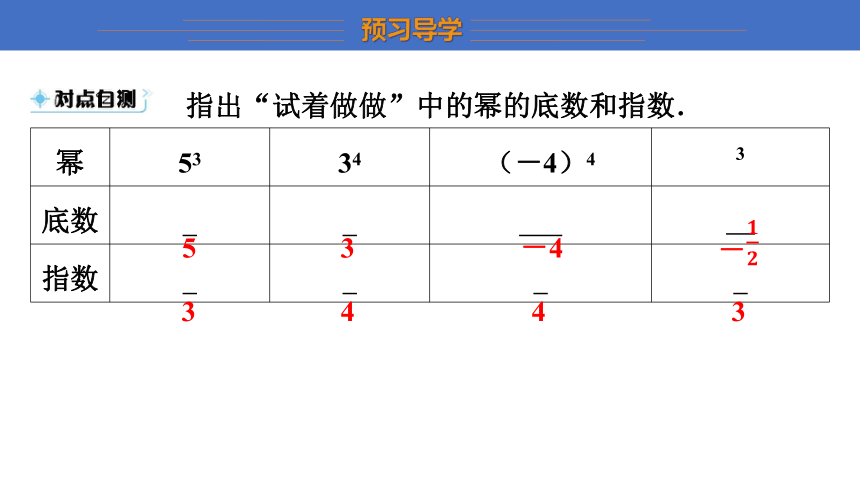
指出“试着做做”中的幂的底数和指数.
幂 53 34 (-4)4 3
底数 5 3 -4 -
指数 3 4 4 3
5
3
-4
-
3
4
4
3
有理数的乘方运算
阅读课本“例”及其解法,回答下面的问题.
(1)结合“例”中的(1)(2),说一说怎样进行有理数的乘方运算?
先根据乘方的意义将乘方转化为乘法,再计算.
(2)-26的底数是多少?它与(-2)6表示的意义相同吗?
-26的底数是2;它表示6个2的乘积的相反数,而(-2)6表示6个-2的乘积,所以它们表示的意义不同.
·导学建议·
第2问特别是-26表示的意义是易错点,教师要特别予以关注.
底数 指数 意义
-an a n n个a的乘积的相反数
(-a)n -a n n个-a的乘积
a
n
n个a的乘积的相反数
-a
n
n个-a的乘积
归纳总结:
幂的符号法则
完成课本“做一做”.
1.-2,4,-8,16,-32,64.
2.当指数是奇数时,幂为负;当指数是偶数时,幂为正.
归纳总结:正数的任何次幂都是 正数 ;负数的奇次幂是 负数 ,负数的偶次幂是 正数 .
(-2)99是 负 数,(-2)100是 正 数.
正数
负数
正数
负
正
有理数的乘方
1.把下列各式写成乘方的形式,并说出底数和指数.
(1)(-6)×(-6)×(-6);(2)×××.
温馨提示:当幂的底数是负数或分数时,底数应该添上括号.
解:(1)原式=(-6)3,底数是-6,指数是3.
(2)原式=()4,底数是,指数是4.
有理数的乘方运算
2.计算:(1)(-4)3;(2)1.52;(3)4;
(4)-43.
解:(1)-64.
(2)2.25.
(3).
(4)-64.
·导学建议·
乘方是乘法的特例,所以乘方运算可以参照乘法的运算来进行.
【方法归纳交流】(易混淆点)有人说:(-a)n与-an一定相等.你认为这种说法正确吗?
解:不正确,可能相等,如(-4)3=-43=-64;也可能互为相反数,如(-2)6=64,-26=-64.
·导学建议·
对于(-a)n与-an,要引导学生从写法、读法、表示的意义等方面加以对比,从而正确区分.
3.计算:(1)-34+(-3)4;(2)-(-3)4.
解:(1)0.
(2)-81.
10的乘方
4.根据乘方的意义,填写下表.
10的乘方 表示的意义 运算结果 结果中0的个数
102 10×10 100 2
103 10×10×10 1000 3
104 10×10×10×10 10000 4
105 10×10×10×10×10 100000 5
10×10×10
1000
3
10×10×10×10
10000
4
10×10×10×10
×10
100000
5
你发现了什么规律?
解:10的几次幂,其结果就有几个0.
【方法归纳交流】10n= 1 .
1
有理数乘方运算的应用
5.将厚0.1毫米的一张纸对折,再对折,这样折4次,其厚度为( D )
A.0.4毫米 B.0.8毫米
C.0.32毫米 D.1.6毫米
D
这是一个很著名的故事:阿基米德与国王下棋,国王输了,国王问阿基米德要什么奖赏,阿基米德对国王说:“我只要在棋盘上第一格放一粒米,第二格放二粒,第三格放四粒,第四格放十六粒……按这个方法放满整个棋盘就行.” 国王以为要不了多少粮食,就随口答应了,结果国王输了.
(2)请探究第(1)题中的数的末位数字是多少?
(3)你知道国王输给了阿基米德多少粒米吗?为解决这个问题,我们先来看下面的解题过程:
题目:用分数表示无限循环小数0..
(1)我们知道,国际象棋共有64个格子,则在第64格中应放多少粒米?(用幂表示)
解:设x=0..①
等式两边同时乘以10,得10x=2..②
将②-①得9x=2,则x=,∴0.=.
请参照以上解法求出国王输给阿基米德的米粒数.(用幂的形式表示)
解:(1)263.
(2)8.
(3)264-1.
第一章 有理数
1.10 有理数的乘方
1.明白乘方的意义,会进行有理数的乘方运算.
2.经历探索幂的符号法则的过程,会判断幂的符号.
◎重点:乘方的意义,幂的符号法则.
◎难点:有理数的乘方运算.
·导学建议·
有理数乘方的意义内容比较简单,可以让学生先自学再讲解,要求:讲清楚乘方、幂、底数、指数的概念及它们之间的关系.
怎样计算边长为5 cm的正方形的面积?怎样计算棱长为3 cm的正方体的体积?
有理数的乘方
1.完成课本“试着做做”.
(1)53,34;(2)(-4)4,3.
2.阅读课本“试着做做”后面的内容,解决下列问题.
(1)求 n个相同因数的积 的运算叫做乘方.例如:= an .
(2)乘方的结果叫做 幂 .在an中,a叫做 底数 ,n叫做 指数 .
(3)an读作什么?与同桌读一读“试着做做”中的幂.
a的n次幂或a的n次方;略.
n个相同因数的积
an
幂
底数
指数
(4)举例说明怎样表示一个数的一次方?
5的一次方可表示为51,通常1省略不写.
·导学建议·
教师要强调指数为1时通常省略不写,但不要误认为指数为0.
指出“试着做做”中的幂的底数和指数.
幂 53 34 (-4)4 3
底数 5 3 -4 -
指数 3 4 4 3
5
3
-4
-
3
4
4
3
有理数的乘方运算
阅读课本“例”及其解法,回答下面的问题.
(1)结合“例”中的(1)(2),说一说怎样进行有理数的乘方运算?
先根据乘方的意义将乘方转化为乘法,再计算.
(2)-26的底数是多少?它与(-2)6表示的意义相同吗?
-26的底数是2;它表示6个2的乘积的相反数,而(-2)6表示6个-2的乘积,所以它们表示的意义不同.
·导学建议·
第2问特别是-26表示的意义是易错点,教师要特别予以关注.
底数 指数 意义
-an a n n个a的乘积的相反数
(-a)n -a n n个-a的乘积
a
n
n个a的乘积的相反数
-a
n
n个-a的乘积
归纳总结:
幂的符号法则
完成课本“做一做”.
1.-2,4,-8,16,-32,64.
2.当指数是奇数时,幂为负;当指数是偶数时,幂为正.
归纳总结:正数的任何次幂都是 正数 ;负数的奇次幂是 负数 ,负数的偶次幂是 正数 .
(-2)99是 负 数,(-2)100是 正 数.
正数
负数
正数
负
正
有理数的乘方
1.把下列各式写成乘方的形式,并说出底数和指数.
(1)(-6)×(-6)×(-6);(2)×××.
温馨提示:当幂的底数是负数或分数时,底数应该添上括号.
解:(1)原式=(-6)3,底数是-6,指数是3.
(2)原式=()4,底数是,指数是4.
有理数的乘方运算
2.计算:(1)(-4)3;(2)1.52;(3)4;
(4)-43.
解:(1)-64.
(2)2.25.
(3).
(4)-64.
·导学建议·
乘方是乘法的特例,所以乘方运算可以参照乘法的运算来进行.
【方法归纳交流】(易混淆点)有人说:(-a)n与-an一定相等.你认为这种说法正确吗?
解:不正确,可能相等,如(-4)3=-43=-64;也可能互为相反数,如(-2)6=64,-26=-64.
·导学建议·
对于(-a)n与-an,要引导学生从写法、读法、表示的意义等方面加以对比,从而正确区分.
3.计算:(1)-34+(-3)4;(2)-(-3)4.
解:(1)0.
(2)-81.
10的乘方
4.根据乘方的意义,填写下表.
10的乘方 表示的意义 运算结果 结果中0的个数
102 10×10 100 2
103 10×10×10 1000 3
104 10×10×10×10 10000 4
105 10×10×10×10×10 100000 5
10×10×10
1000
3
10×10×10×10
10000
4
10×10×10×10
×10
100000
5
你发现了什么规律?
解:10的几次幂,其结果就有几个0.
【方法归纳交流】10n= 1 .
1
有理数乘方运算的应用
5.将厚0.1毫米的一张纸对折,再对折,这样折4次,其厚度为( D )
A.0.4毫米 B.0.8毫米
C.0.32毫米 D.1.6毫米
D
这是一个很著名的故事:阿基米德与国王下棋,国王输了,国王问阿基米德要什么奖赏,阿基米德对国王说:“我只要在棋盘上第一格放一粒米,第二格放二粒,第三格放四粒,第四格放十六粒……按这个方法放满整个棋盘就行.” 国王以为要不了多少粮食,就随口答应了,结果国王输了.
(2)请探究第(1)题中的数的末位数字是多少?
(3)你知道国王输给了阿基米德多少粒米吗?为解决这个问题,我们先来看下面的解题过程:
题目:用分数表示无限循环小数0..
(1)我们知道,国际象棋共有64个格子,则在第64格中应放多少粒米?(用幂表示)
解:设x=0..①
等式两边同时乘以10,得10x=2..②
将②-①得9x=2,则x=,∴0.=.
请参照以上解法求出国王输给阿基米德的米粒数.(用幂的形式表示)
解:(1)263.
(2)8.
(3)264-1.
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
