函数的表示法
图片预览


文档简介
课件11张PPT。1.2.2函数的表示法函数的概念:复习回顾 设A、B是两个 ,如果按某个确的
对应关系f,使对于集合A中的 x,在集
合B中都有 和它相对应,那么就
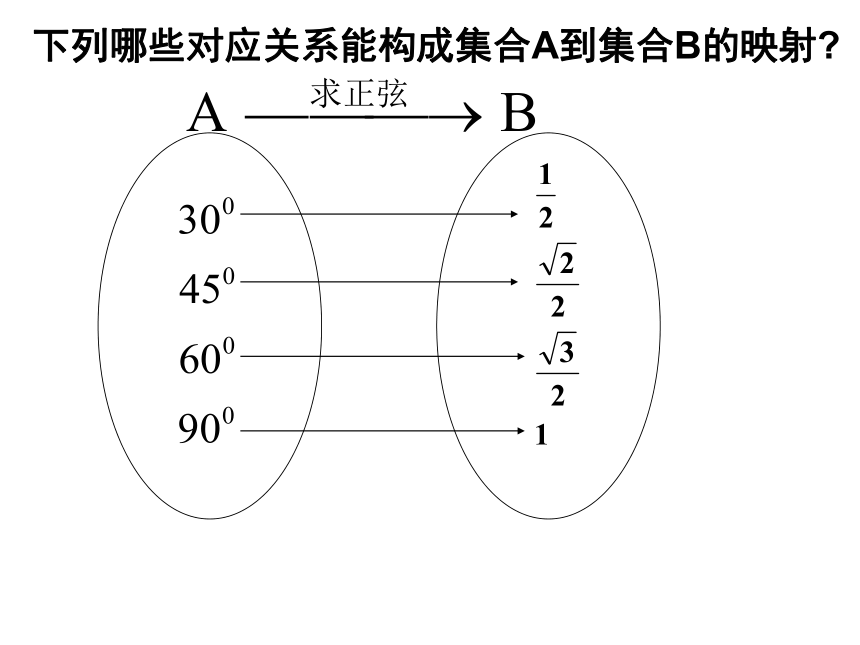
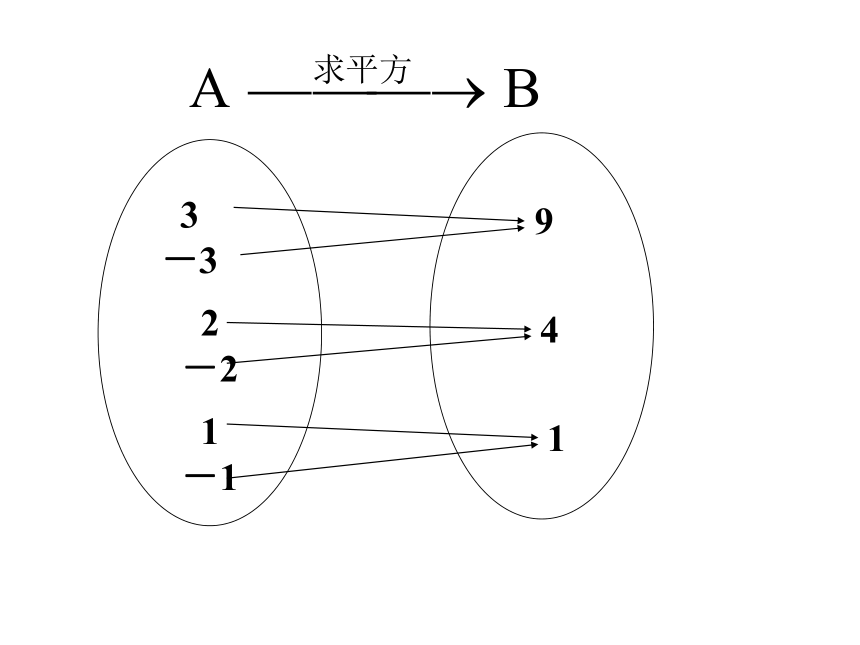
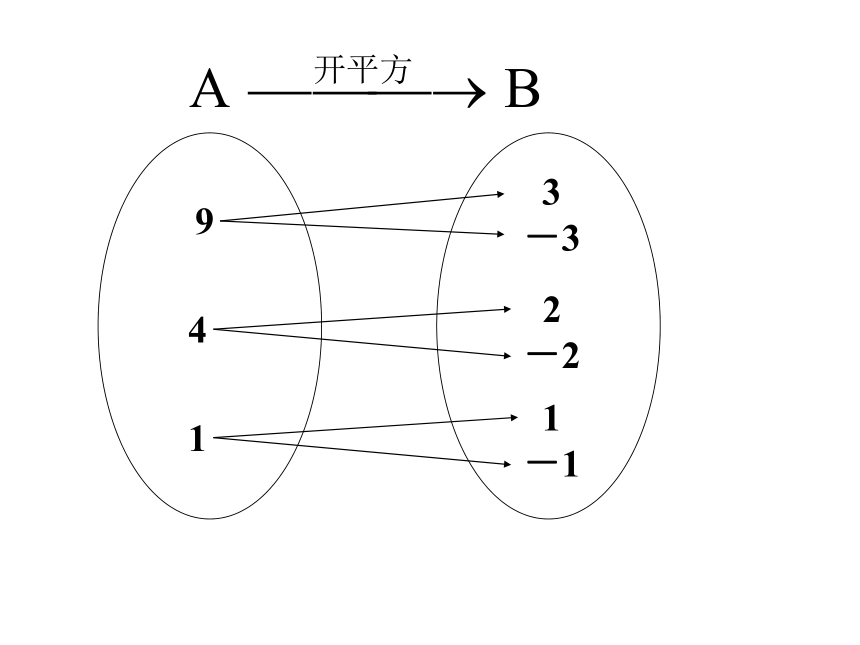
称f:A→B为从集合A到集合B的一个 .非空数集任意一个数唯一确定的数f(x)函数非空的集合任意一个元素唯一确定的元素映射映射的概念: 由此可知,映射是函数的推广,函数是一种特殊的映射。下列哪些对应关系能构成集合A到集合B的映射?3
-32
-21
-19419413
-32
-21
-11
2
3
4
5
6
1
2
3
4
12
200
1
2
3
4
5通过以上几个实例,谈谈你对映射f:A→B是怎么理解的?1、A中每个元素在B中必有唯一的元素与之对应;2、对A中不同的元素,在B中可以有相同的元素与它 对应;4、A中无空余元素,允许B中有空余元素3、A中元素与B中元素的对应关系,可以是:一对一,多对一,但不能一对多例7 以下给出的对应是不是从集合A到B的映射?
(1)集合A={P|P是数轴上的点},集合B=R,
对应关系f:数轴上的点与它所代表的实数对应;
(2)集合A={P|P是平面直角坐标系中的点},集合B= ,对应关系f:平面直角坐标系中的点与它的坐标对应;
(3)集合A={x|x是三角形},集合B={x|x是圆}对应关系f:每一个三角形都对应它的内切圆;
(4)集合A={x|x是新华中学的班级},集合B={x|x是新华中学的学生},
对应关系f:每一个班级都对应班里的学生;变式: 以下给出的对应是不是从集合B到集合A 的映射?
(3)集合A={x|x是三角形},集合B={x|x是圆},
对应关系f:每一个圆都对应它的内接三角形;
(4)集合A={x|x是新华中学的班级},集合B={x|x是新华中学的学生},
对应关系f:每一个学生都对应它的班级.例8 已知集合A={a1,a2,a3}, B={b1,b2},问可
以建立从A到B的不同映射多少个?结论:对于从n个元素集合到m个元素集合的
映射,最多可以建立 个不同的映射.变式:问可以建立从B到A的不同映射多少个?mn
对应关系f,使对于集合A中的 x,在集
合B中都有 和它相对应,那么就
称f:A→B为从集合A到集合B的一个 .非空数集任意一个数唯一确定的数f(x)函数非空的集合任意一个元素唯一确定的元素映射映射的概念: 由此可知,映射是函数的推广,函数是一种特殊的映射。下列哪些对应关系能构成集合A到集合B的映射?3
-32
-21
-19419413
-32
-21
-11
2
3
4
5
6
1
2
3
4
12
200
1
2
3
4
5通过以上几个实例,谈谈你对映射f:A→B是怎么理解的?1、A中每个元素在B中必有唯一的元素与之对应;2、对A中不同的元素,在B中可以有相同的元素与它 对应;4、A中无空余元素,允许B中有空余元素3、A中元素与B中元素的对应关系,可以是:一对一,多对一,但不能一对多例7 以下给出的对应是不是从集合A到B的映射?
(1)集合A={P|P是数轴上的点},集合B=R,
对应关系f:数轴上的点与它所代表的实数对应;
(2)集合A={P|P是平面直角坐标系中的点},集合B= ,对应关系f:平面直角坐标系中的点与它的坐标对应;
(3)集合A={x|x是三角形},集合B={x|x是圆}对应关系f:每一个三角形都对应它的内切圆;
(4)集合A={x|x是新华中学的班级},集合B={x|x是新华中学的学生},
对应关系f:每一个班级都对应班里的学生;变式: 以下给出的对应是不是从集合B到集合A 的映射?
(3)集合A={x|x是三角形},集合B={x|x是圆},
对应关系f:每一个圆都对应它的内接三角形;
(4)集合A={x|x是新华中学的班级},集合B={x|x是新华中学的学生},
对应关系f:每一个学生都对应它的班级.例8 已知集合A={a1,a2,a3}, B={b1,b2},问可
以建立从A到B的不同映射多少个?结论:对于从n个元素集合到m个元素集合的
映射,最多可以建立 个不同的映射.变式:问可以建立从B到A的不同映射多少个?mn
